摆线的参数方程

建立两个平面直角坐标系，一个是固定系\(O\)，另一个是不定系\(O’\)，二者初始状态完全重合，置于一个半径为\(R\)的圆，圆上取其一点v\(\begin{pmatrix} 0& -R\end{pmatrix}^T\)

旋转与平移矩阵——左乘矩阵

矢量u应升级为\(\begin{pmatrix} x& y&1\end{pmatrix}^T\)

1.对于固定系\(O\)而言，矢量u绕\(O\)顺时针\(\theta\)的旋转矩阵\(R\)

\[R=\begin{pmatrix} cos{\theta} & sin{\theta} & 0\\ -sin{\theta} & cos{\theta} & 0\\ 0 & 0 & 1\end{pmatrix} \]

2.对于固定系\(O\)而言，矢量u沿着\(x\)正方向平移\(dx\)且沿\(y\)正方向平移\(dy\)的平移矩阵\(T\)

\[T=\begin{pmatrix} 1 & 0 & dx\\ 0 & 1 & dy\\ 0 & 0 & 1\end{pmatrix} \]

摆线方程推导

摆线：圆沿着直线无滑动旋转，圆上固定一点(二维)所形成的轨迹

对于点\(v\)升级（三维）为\(\begin{pmatrix} 0& -R&1\end{pmatrix}^T\)，摆线获取的等价过程：圆绕\(O\)旋转\(\theta\)，再沿\(y\)正方向平移\(R\)，再沿\(x\)正方形平移\(R\theta\)，点\(v\)形成的轨迹即时摆线

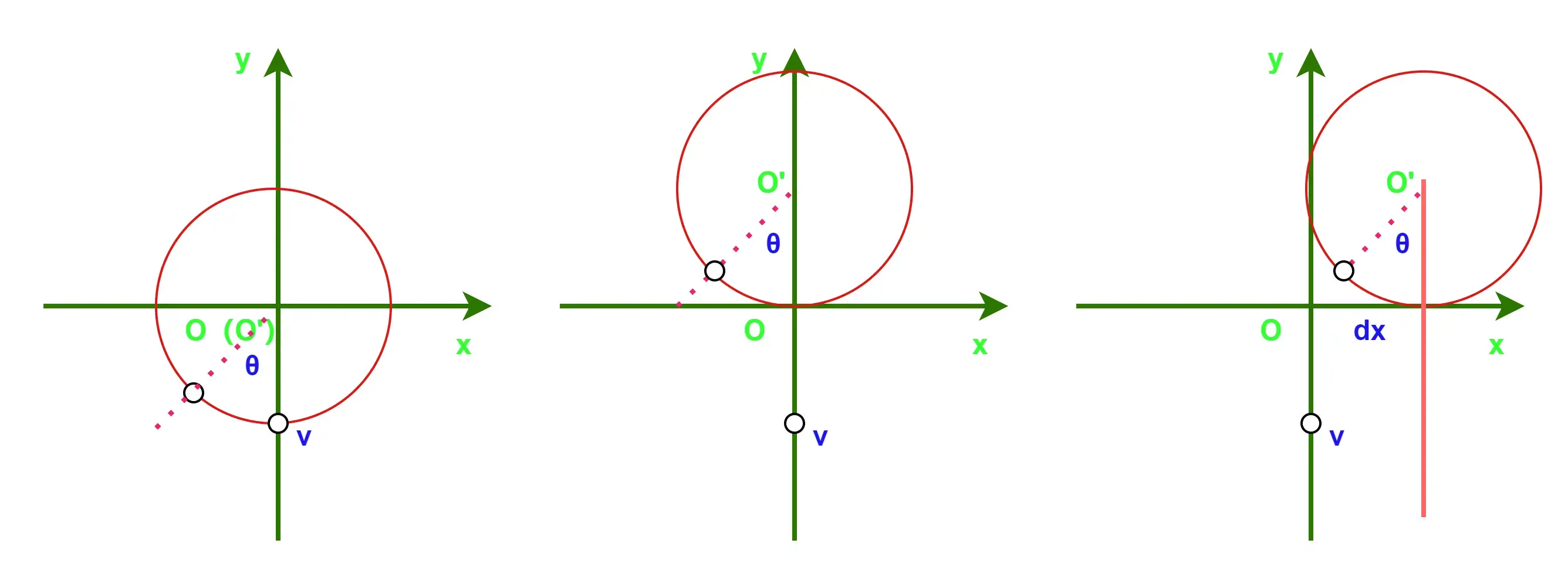
摆线轨迹方程\(F:\begin{pmatrix} x& y&1\end{pmatrix}^T\)，有\(F=T*R*v\)，\(\theta∈[0,2\pi]\)

\[\begin{pmatrix} x\\ y\\1\end{pmatrix}=\begin{pmatrix} 1 & 0 & R\theta\\ 0 & 1 & R\\ 0 & 0 & 1\end{pmatrix}*\begin{pmatrix} cos{\theta} & sin{\theta} & 0\\ -sin{\theta} & cos{\theta} & 0\\ 0 & 0 & 1\end{pmatrix}*\begin{pmatrix} 0\\ -R\\1\end{pmatrix} \]

故

\[\left\{\begin{matrix} x=R(\theta-sin\theta)\\ y=R(1-cos\theta) \end{matrix}\right.\]

其实第三阶段可以直接推导出参数方程

来源链接：https://www.cnblogs.com/invo/p/18632730