搜索算法合集
By DijkstraPhoenix
深度优先搜索 (DFS)
引入
如果现在有一个迷宫，如何走路径最短？
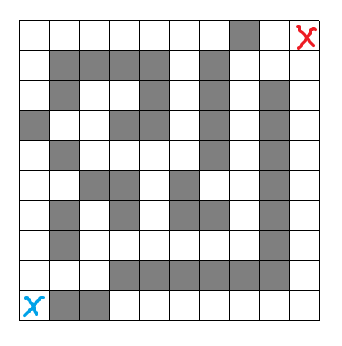
方法
走迷宫最简单粗暴的方法式什么呢？当然是把所有路都走一遍啦！
如果是手动计算的话，可能会把你手指累得抽筋，但电脑不会，电脑具有强大的算力，这种暴力的事情当然是交给电脑做啦。
深搜的本质：一条路走到底，走到死胡同再往回走，回到上一个岔口继续走，直到找到正确的路
实际上，任何一条路都可以看做是一个只有一个岔口的分岔路，所以不需要把路和岔口分开计算。
那么刚才的例子应该是这么走（数字代表第几次尝试）实际上岔口走的顺序是任意的，方法不唯一。
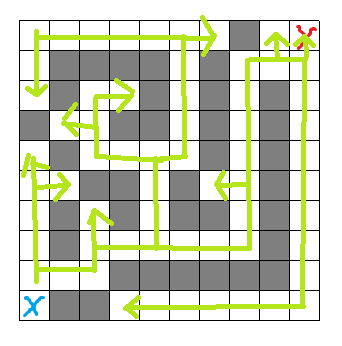
概念：从死胡同返回的步骤叫做回溯
由于深搜不能保证第一次找到的路径为最短路径，所以需要统计所有路线
深搜一般使用递归实现，走过的每个位置都要打上标记，同一条路不能再走一遍
四联通和八连通：
有些走迷宫题目是四联通的（即上下左右），也有些是八连通的（即上、下、左、右、左上、左下、右上、右下），需要仔细观察题目要求
四联通位移数组：dx[]={1,0,-1,0}; dy[]={0,1,0,-1};
八连通位移数组：dx[]={1,0,-1,0,1,1,-1,-1}; dy[]={0,1,0,-1,1,-1,1,-1};
主算法代码:
int maze[MAXN][MAXN];//存储迷宫 0表示当前节点可以走，1表示不能走
bool vis[MAXN][MAXN];//打标记
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};//位移数组，分别对应 上右下左（如果是八向移动的话要改成对应的）
int n,m,stx,sty,edx,edy;//地图长宽以及起点和终点的坐标
int ans=0x7f7f7f7f;//最短距离，要初始化为极大值
void dfs(int x,int y,int z)//x和y是当前位置的坐标，z是走过的步数
{
if(x==edx&&y==edy)//到了终点
{
ans=min(ans,z);//更新答案（如果答案还是极大值，说明无法到达终点）
return;
}
vis[x][y]=true;//打标记
for(int i=0;i<4;i++)//枚举四个方向
{
int nx=x+dx[i],ny=y+dy[i];//下一个应该走到的位置
if(nx<1||nx>n||ny<1||ny>m)continue;//不能走出地图（这个要写在灵魂拷问的最前面，否则访问数组要越界）
if(maze[nx][ny]==1)continue;//不能卡墙里
if(vis[nx][ny])continue;//不能走你走过的路
dfs(nx,ny,z+1);//走到下一个节点
}
vis[x][y]=false;//重点！回溯时要清除标记！
}
例题
连通块问题
求1的连通块数量
这是一类重要的题目！
本题可以使用 DFS 从每一个点开始将每一个连通块都标记并计数
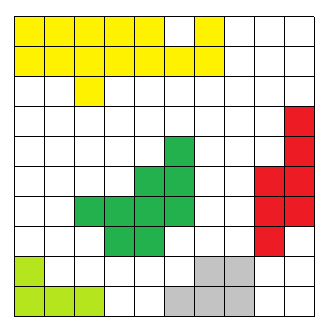
上图就是标记出的连通块
我们可以从连通块的任意一个位置开始，遍历整个连通块，并把这个连通块的所有点打上标记（防止重复计算）
这个方法也叫洪水填充法(Flood Fill)
强烈建议在网上找几篇专门讲连通块的博客学一下
#include<bits/stdc++.h>
using namespace std;
int maze[105][105];
bool vis[105][105];
int n,m,ans;
void dfs(int x,int y)
{
vis[x][y]=true;
for(int i=0;i<4;i++)
{
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m)continue;
if(maze[nx][ny]!=1)continue;
if(vis[nx][ny])continue;
dfs(nx,ny);
}
//注意！！！此处不要回溯（标记是给后面的连通块看的）
}
int main(void)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
cin>>maze[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(!vis[i][j]&&maze[i][j]==1)//如果这个点没找过并且是连通块的一部分，那么就是一个新的连通块
{
ans++;
dfs(i,j);//为整个连通块打上标记
}
}
}
cout<<ans;
return 0;
}
八皇后问题
本题的每一步都决定一个皇后的位置，由输出格式就可以看出，我们可以按每一列的顺序计算。一个皇后会独占一行、一列、两斜线，因为是按列计算的，不需要给列打标记，则需要 3 个标记数组。
（其实可以看一下洛谷上的题解）
#include<bits/stdc++.h>
using namespace std;
bool vis[15],vis1[35],vis2[35];
int n;
int nod[15];
int sum=0;
void dfs(int k)
{
if(k>n)
{
sum++;
if(sum<=3)//前3个要输出方案
{
for(int i=1;i<=n;i++)cout<<nod[i]<<" ";
cout<<endl;
}
return;
}
for(int i=1;i<=n;i++)
{
if(vis[i])continue;
if(vis1[i+k-1])continue;
if(vis2[i-k+13])continue;
vis[i]=true;
vis1[i+k-1]=true;
vis2[i-k+13]=true;//可以手动模拟一下行列坐标和斜坐标的关系，加13是防止计算出负数
nod[k]=i;//保存方案
dfs(k+1);
vis[i]=false;
vis1[i+k-1]=false;
vis2[i-k+13]=false;
}
}
int main(void)
{
cin>>n;
dfs(1);
cout<<sum;
return 0;
}
全排列问题
这是一个重要的题目！
按照题意模拟搜索即可
#include<iostream>
#include<cstdio>
using namespace std;
int n,a[1000],vis[1000];
void dfs(int step)
{
if(step==n+1)
{
for(int i=1;i<=n;i++)
{
printf("%5d",a[i]);//题目要求格式化输出
}
cout<<endl;
}
for(int i=1;i<=n;i++)
{
if(vis[i]==1)continue;
a[step]=i;
vis[i]=1;
dfs(step+1);
vis[i]=0;
}
}
int main(void)
{
cin>>n;
dfs(1);
return 0;
}
一些建议练习的题
求细胞数量
提示：联通块问题，不要清除标记，从每个未标记且是细胞的块出发，将整个块打上标记
广度优先搜索 (BFS)
引入
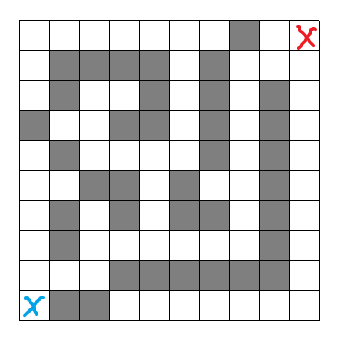
还是刚才的迷宫问题
方法
除了把每一条路走一遍，其实还可以用水把迷宫给淹了。这样可以顺着水找到路径。
BFS 模拟洪水往外扩散的样子，按层遍历。
这样做有一个好处：如果像迷宫这样，每两个相邻的方块之间的距离都一样的话，第一次找到的路径就是最短路径（每一层走过的路程都一样），如果没有这个条件就不保证最短
以下是 BFS 和 DFS 策略上的对比：
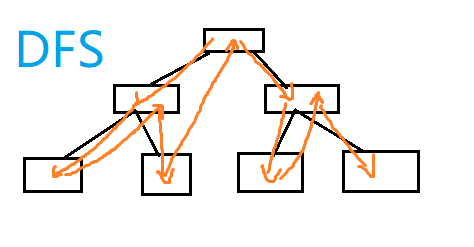
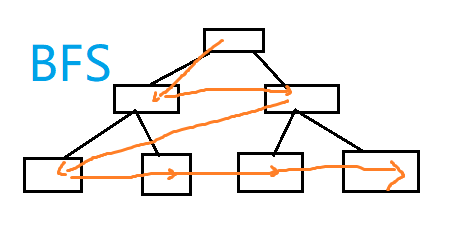
放到迷宫里就是这个样子：
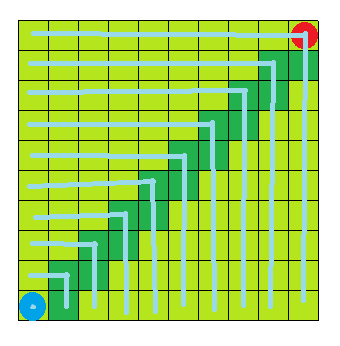
(图中深绿色代表路径，浅绿色代表访问过的点，线表示遍历的每一层)
重点！因为同一层的点无法直接像 DFS 那样转移，所以会把应该访问的节点放到一个队列里，挨个处理
主要代码:
struct node
{
int x,y,step;//节点坐标和已经走过的步数
};
queue<node>Q; //队列
bool vis[MAXN][MAXN];//标记数组
int maze[MAXN][MAXN];//存储地图，0可以走，1不能走
int stx,sty,edx,edy;
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};
int n,m;//地图长宽
void bfs(void)//bfs其实不需要封装在函数里，它不需要递归
{
Q.push(node{stx,sty,0});
vis[stx][sty]=true;//初始状态
while(!Q.empty())//直到所有的状态都处理完毕
{
int x=Q.front().x,y=Q.front().y,st=Q.front().step;//取出队首元素
Q.pop();//很重要！不要忘了出队列
for(int i=0;i<4;i++)
{
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m)continue;
if(vis[nx][ny])continue;
if(maze[nx][ny]==1)continue;//灵魂三问
Q.push(node{nx,ny,st+1});//加入处理队列
vis[nx][ny]=true;//打标记 注意！BFS没有回溯！
if(nx==edx&&ny==edy)//到终点了
{
cout<<st+1;
return 0;
}
}
}
}
例题
Catch That Cow S
本题的转移有三种：前进1步，后退1步，乘2
其实本题代码很简单（别看有点长）实际上是三个转移
#include<bits/stdc++.h>
using namespace std;
int t,x,y;
bool vis[100005];
queue<int>Q,step;
int main(void)
{
cin>>t;
for(int test(1);test<=t;test++)
{
cin>>x>>y;
Q.push(x); //入队
step.push(0); //初始他一步也没走，step入队0
vis[x]=true; //标记
while(!Q.empty()) //step和Q是同步的，不需要额外判断
{
//取队首元素
int s=Q.front();
int st=step.front();
Q.pop(); //出队
step.pop();
int nst=st+1;
int ns;
//找可以的情况
ns=s+1;//前进1步
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径，直接输出
cout<<nst;
break;
}
}
ns=s-1;//后退1步
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径，直接输出
cout<<nst;
break;
}
}
ns=s*2;//乘2
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径，直接输出
cout<<nst;
break;
}
}
}
}
}
字串变换
本题需要寻找可以变换的部分进行转移。字符串长度不长，可以暴力配对
#include<bits/stdc++.h>
using namespace std;
#define int long long
string ap[25],bp[25];
int le;
queue<string>q;
queue<int>step;//本代码没有使用结构体而是使用两个队列
map<string,bool>vis;
signed main(void)
{
string a,b;
string ia,ib;
cin>>a>>b;
while(cin>>ia)
{
cin>>ib;
ap[++le]=ia;
bp[le]=ib;
}
q.push(a);
step.push(0);
vis[a]=true;
while(!q.empty())
{
string s=q.front();q.pop();
int st=step.front();step.pop();
if(st==10)continue;
for(int i=1;i<=le;i++)
{
int start=0;
while(true)
{
int fd=s.find(ap[i],start);//寻找匹配字符串
if(fd==string::npos)break;
start=fd+1;
string tmp=s.substr(0,fd);
tmp+=bp[i];
tmp+=s.substr(fd+ap[i].length());
if(vis[tmp])continue;
q.push(tmp);//转移
step.push(st+1);
if(tmp==b)//找到了
{
cout<<st+1;
return 0;
}
}
}
}
cout<<"NO ANSWER!";
return 0;
}
一些建议的题
–还没写完呢–
© 版权声明
本站所有资源来自于网络，仅供学习与参考，请勿用于商业用途，否则产生的一切后果将由您(转载者)自己承担！
如有侵犯您的版权，请及时联系3500663466#qq.com(#换@)，我们将第一时间删除本站数据。
如有侵犯您的版权，请及时联系3500663466#qq.com(#换@)，我们将第一时间删除本站数据。
THE END
暂无评论内容