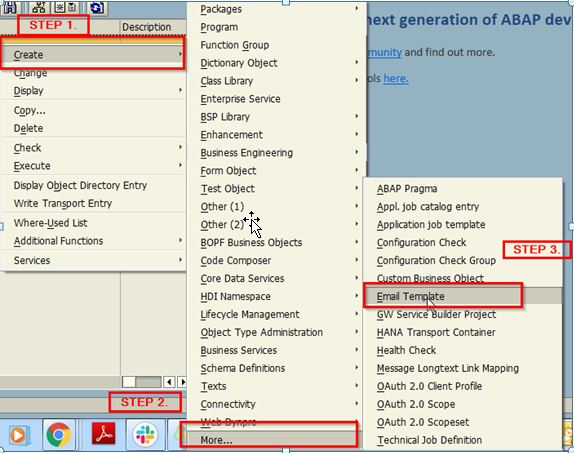
1、首先明确一个概念
C语言中整形是按照二进制存储在内存中,浮点型是按科学计数法存储在内存中(本质上存储的还是二进制数据0和1)。
如果没看懂这句话,没关系!看完以下正文,你就会豁然开朗!并且预先提出两个问题:
1)为什么浮点型不能执行位运算?
2)浮点型数据转换为整形数据时,编译器内部做了什么样的处理?
2、接下来,讲解C语言中浮点型数存储的规则
c语言中的浮点型有如下几种 (float ,double ,longdouble),因为不同系统平台下数据类型的长度会不一样,这里我们统一在32位GCC编译器下, float=4Byte,double=8个Byte
先定义
float num_1=10.5f; /* 这里有个小知识点,很多编译器中,如果10.5后面不加f(小写),会默认为存储为double类型*/ double num_2 = 11.5
根据国际电器和电子工程协会,标准IEEE754规定,浮点数可以按照以下规则存储
(-1)^S*M*2^E
2.1、可以将上述公式分为两部分来看
(-1)^S是确定数字是整数还是负数。M*2^E确定的数字绝对值的大小。
- 这里的M必须是二进制数。有些资料把M叫做尾数
- S必须是整数1,或整数0。有些资料把S叫做数符
- E也必须是>=0的整数。有些资料把E叫做阶码
结合图形来看:

C语言存储浮点型数据float时,会将内存分为三个区域。结合实例我们来看
float num_1=10.5,先转换为IEEE754格式,首先该数为正数故s=0;(-1)^0=0,符号位=0,表示正数。
- 第1步:在把10.5转换为科学计数法 1.05*10^1,
- 第2步:再把10.5二进制格式,其中M要为二进制数据,dec(10.5)=bin(1010.1)
- 第3步:二进制写成科学计数法10.5=1010.1*2^0 = 1.0101*2^3。
10.5为正数于是 31符号位S=0、E=3 =0000 0011 。有效数字M=1.0101。但是如果你按上述来写,肯定是错误的。浮点数存储时,还要遵守一定的转换方式:转换规则如下(也是很重要的一个知识点)
(规则1)1<=M<2。IEEE 754规定 M只存储小数部分,于是10.5只会存储0101,系统会默认最高位为1(。
(规则2)而E,存储时:
- float类型数据,存储值=E+127.
- double类型数据,存储值=E+1023.
首先得明确是一个无符号数,10.5=1.0101*2^3,E=3,二进制表示为 0000 0011。IEEE754规定了。对于32bit长度的float类型。E需要加上127,在此得到的数,再存储到内存中去,我们把这个值叫做E的存储值。3+127=129=1000 0010。double类型,应该加上1023。至于为什么,后面细说。

M的0101,应该左移到22-19bit位处
于是10.5的正确格式应该是上图所示的格式。
至于E为什么要+127(float)+1023(double),下面会介绍。
2.2、问:十进制小数0.5该如何存储?
转换为二进制科学计数法1*2^-1。如果我们E不做处理。
将会有如下问题,s=0,没有问题,E=-1,E是无符号数,不能显示为-1。M存储的是小数部分,全部存储为0。
故:为了解决E无法表示负数的问题,才引入了E+127(Float),和E+1023(double)。为了描述方便,下面统一以float类型为例,当E存储值<127时,认定E为负数,如E存储值为125,则E的实际值为-2。当E的存储值>127时,E的真实值为正数,130=3。以此类推。。。。
故,本质上E存储时需要+127或+1023是为了解决浮点数,(-1,1)注意是不包含边界数的关系,的存储问题。
E不全为0或不全为1
比如:
- 0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其E为-1+127=126,表示为:
- 01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进 制表示形式为:
- 0 01111110 000000000000000000000001
另外还有两种比较特殊的情况,E全为0和E全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1。
E全为0
- 这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于 0的很小的数字。
E全为1
- 这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
2.3 浮点数存储时的误差
float Val_1=0.6f;
此时我们算一下,常量0.6f是如何存储的。使用2进制来表示的话,我们知道2^-1=0.5、2^-2=0.25、2^-3=0.125、2^-4=0.0625……
故我们使用0.1b=0.5,还需要表示出10进制的小数0.1。从上面的例子也可以看出,实际上浮点数存储时,是无法准确的表示出0.1的。所以只能采取一种无限逼近的方法,0.6的二进制表示是0.1001100110011…(无限循环),如果需要有限位数的表示,可以根据需要选择适当的位数进行截取。例如,取4位小数,则表示为0.1001。使用二进制科学计数法为1.001*2^-1.
存储时:
S=0; E=-1+126=125; M=001
3、回答一开始提出的两个问题
3.1、为什么浮点数不能执行位运算;
答:整形执行位运算,准确的来说是无符号整形,才能执行位运算
- 移位运算:<<和>>
- 左移,一位相当于数字*2(加倍)
- 右移,相当于数字/2
根据浮点数的结构来看,浮点数,明显是达不到这样的效果的。
大家拿起笔,思考一下,浮点数执行,按位与&,按位或|,按位异或等运算时,是何种情况?。
3.2、浮点型数据转换为整形数据时,编译器内部做了什么样的处理?
答:
#include <stdio.h>
#include <stdlib.h>
int main()
{ int a=1090;
float b=1020.23;
a=b;
printf("a的值为%d:",a);
return 0;
}
看输出结果:

看起来是似乎很合理?浮点数直接去掉小数部分,直接将自己的整数部分,赋值给了整形数据.其实编译器是先将浮点数值算出来,再截取整数部分截取给整形数据。
4、浮点数如何转换为整型
浮点数可以通过舍去小数部分或四舍五入的方式转换为整型。
舍去小数部分:
可以使用math.floor()函数,该函数返回一个不大于浮点数的最大整数。例如:
num = 3.14 integer = math.floor(num) # 此时integer的值为3
四舍五入:
可以使用round()函数,该函数返回一个最接近的整数,如果有两个整数与浮点数的距离相等,则返回偶数。例如:
num = 3.14 integer = round(num) # 此时integer的值为3
需要注意的是,转换为整型可能会导致数据精度的损失。
总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持脚本之家。
来源链接:https://www.jb51.net/program/337724zj0.htm
如有侵犯您的版权,请及时联系3500663466#qq.com(#换@),我们将第一时间删除本站数据。







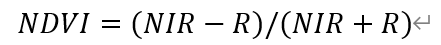




暂无评论内容