一维前缀和
具体做法:
首先做一个预处理,定义一个sum[]数组,sum[i]代表a数组中前i个数的和。
原理:
sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l+1] ...... a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1]+......+ a[r];
图解

求前缀和运算:
const int N = 1e5+10;
int sum[N], a[N]; //sum[i] = a[1] + a[2] + a[3] ..... a[i];
for(int i = 1; i <= n;i++)
{
sum[i] = sum[i - 1] + a[i];
}
总结

一维前缀和模板题
二维前缀和
推导
如图
![图片[1]-前缀和-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/03/6525541621804552268.jpg)
紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。
从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] – 重复加的红色的面积s[i-1][j-1] + 小方块的面积a[i][j];
![图片[2]-前缀和-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/03/8581601937477001449.jpg)
因此得出二维前缀和预处理公式
s[i][j] = s[i-1][j] + s[i][j-1] + a[i][j] - s[i-1][j-1]
接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。
如图
![图片[3]-前缀和-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/03/460100692936135555.jpg)
紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ,黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积;
不难推出:
![图片[4]-前缀和-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/03/6202904404413910319.jpg)
绿色矩形的面积 = 整个外围面积s[x2, y2] – 黄色面积s[x2, y1 - 1] – 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]
总结

二维前缀和模板题
来源链接:https://www.cnblogs.com/liqs2526/p/18758483
如有侵犯您的版权,请及时联系3500663466#qq.com(#换@),我们将第一时间删除本站数据。
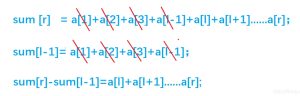
















暂无评论内容