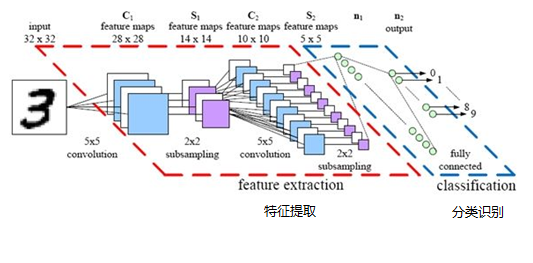
1. 全连接层

前文中我们讨论的几乎都是全连接层，也就是在层间，每个神经元都与前一层的所有神经元相连接，如图：

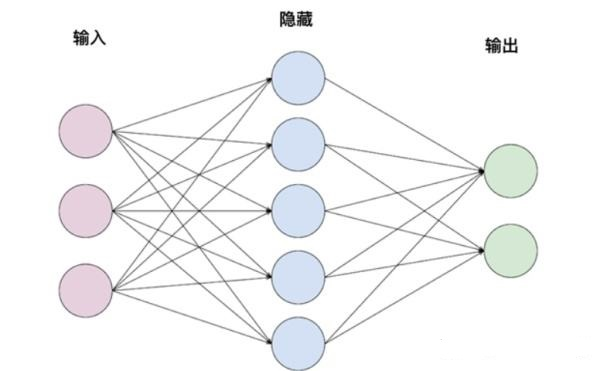
也就是每层的每个feature，都与前一层所有features相关联，是前一层所有features乘以一个权重矩阵W得来的。（这里为了简化理解，我们暂不考虑bias，activation function）。

如果我们用MNIST数据集，图片是28X28的，输入全连接层时就要将其进行一维化，变成1X784个输入节点，图片就变成了类似这样：

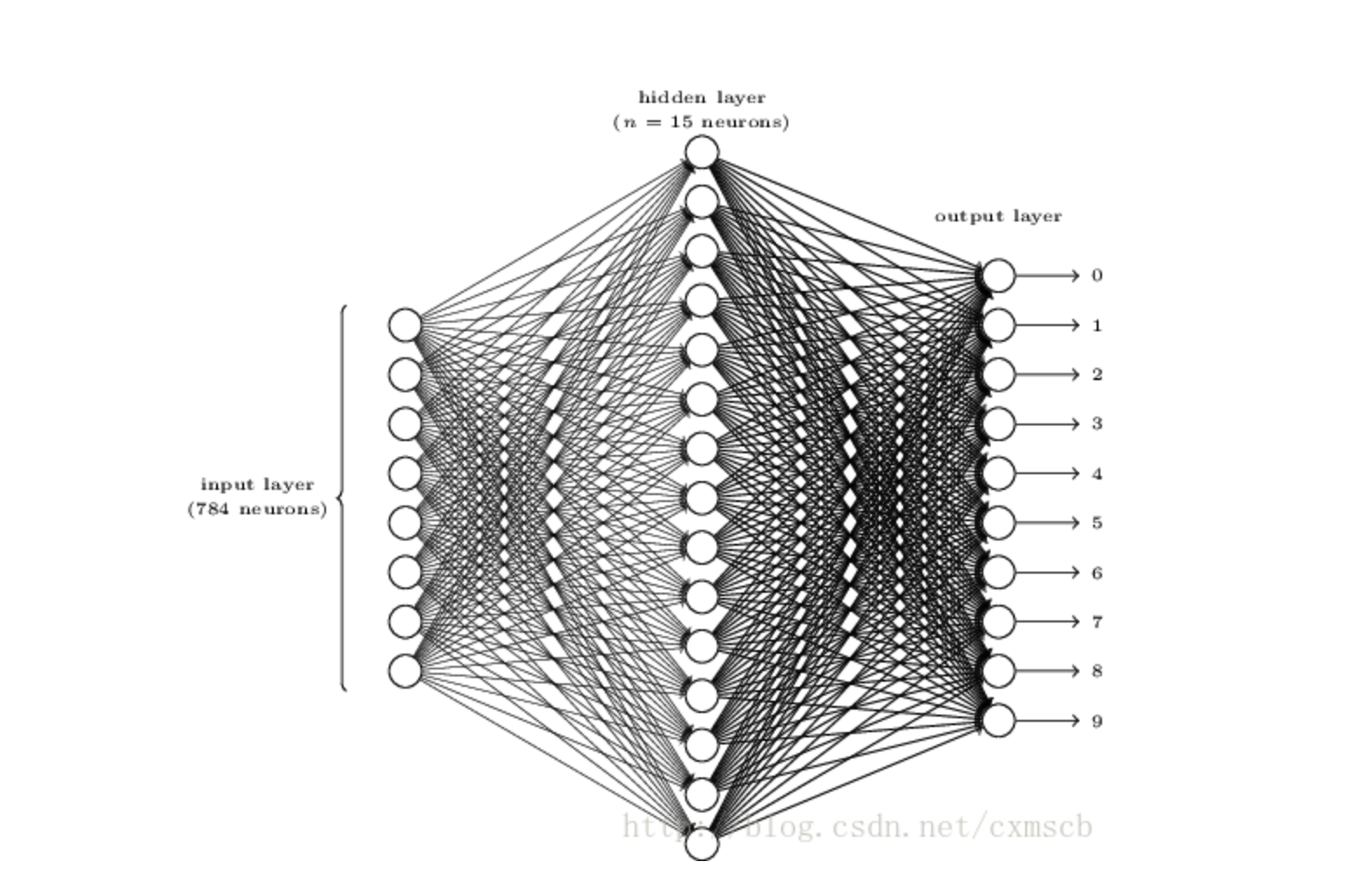
这里我们遇到了几个问题：

1. 是不是每一个特征都有必要和前一层所有特征相关联
2. 一维化的操作感觉很粗暴，会不会丢失了某些信息
3. 这么多的权重数据，网络是不是太复杂了，会过拟合吗，训练起来消耗是否很大

对于第一个问题，每一个特征事实上只需要和部分前一层的特征相关联，尤其是对于图片这种具有“空间位置信息”的数据来说，每一个特征更有可能是通过在空间位置上距离较近的一组特征（图片上某处的局部像素信息）得到的。反之，图片左上角某个像素和图片右下角某个像素是不大可能共同作用出什么有效特征的。在全连接网络中，我们当然可以寄希望于神经网络自动的提取出有效特征，自动把无效的连接权重训练为0，然而这无疑加重了训练难度，如果我们知道某些先验信息（图片的空间信息特点），何必让神经网络加重学习负担呢。

对于第二个问题，同样的，对于图片来说，一维化操作使得空间特征信息丢失掉了，我们只能期望神经网络自己学习到这些空间信息，从而把与空间信息相关的特征学习到，然而这是非常低效的方法。

对于第三个问题，全连接网络的参数量非常大，随着图片像素提升，这种一维化的操作带来的计算开销是非常大的。此外，网络的复杂结构还很有可能产生过拟合现象。甚至我们还得通过dropout的方式手动的减少一些它们之间的连接。因此，这种复杂性是没必要的。

那么对于类似图片这种具有“空间位置信息”，有没有方法能够只关联必要的特征，保留空间位置信息，又能简化网络复杂性呢。

答案就是卷积神经网络。

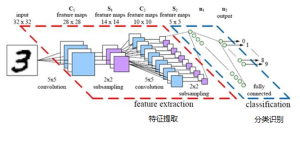
2. 卷积神经网络

网络上介绍卷积算法的文章非常多，计算也比较简单，这里我截了一张图来示意：

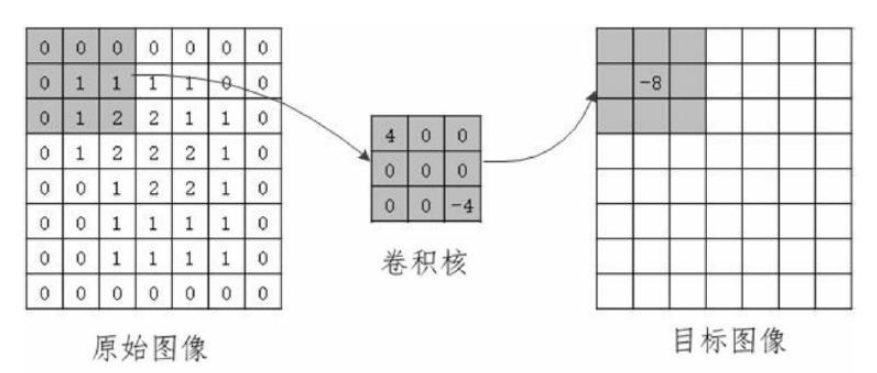
我们把卷积核看作一个指定窗口大小的扫描器，扫描器在原始图像上进行滑动，每次都与相对应的原始图像上的相同大小的局部区域进行卷积运算，也就是加权运算，得到目标图像上的一个像素。也就是说，目标图像上的这个特征，只与原始图像上的一组局部特征相关联。由于我们没有对原始图像进行一维化操作，空间信息保留了下来。同时，随着卷积核的滑动，卷积核在本次扫描过程中，其参数是不变的，也就是对于目标图像的每个特征，其计算权重是一样的，也就是权值共享的概念，这也大大降低了模型的复杂度。且，这种降低模型复杂度的操作是有效而有意义的（不同于dropout那种是完全随机的）。
上面的三个问题得到了很好的解决。

两个小细节：

1. 如果卷积核为3X3，那么目标图像的一条边上的像素数量会比原始图形少2，特征图缩小了一些，如果要保持不变，就需要进行padding
2. 扫描器滑动的时候可以设置步长，即每次滑动过的像素数量。

2.1 与全连接层的关系

我们比对全连接和卷积网络，其本质都是每一个特征是由前一层特征加权得到，区别就是全连接是所有特征的加权，且权重系数不同；卷积，是空间局部特征的加权，且权重系数共享。

全连接网络，我们要训练的是权重矩阵W；卷积网络中，我们要训练的是卷积核。

2.2 与传统图像领域的卷积核关系

传统图像领域中的卷积核，是通过图像领域知识得到的，比如边缘检测、纹理检测等。我们明确的知道使用什么样的卷积核数值去提取意义明确的特征；而卷积神经网络中，卷积核的数值是随机初始化的，是要通过神经网络的训练去优化卷积核，从而提取到“有用的”特征的。这里的我们往往只是知道它有用，但不明确它的具体意义。这也就是为什么我们通常认为神经网络是“黑盒”的原因。
虽然我们不知道具体意义，但我们还是能够知道在神经网络中的特征的一般规律：通常来说，靠近输入端的浅层神经网络提取到的往往是比较底层的信息，比如边缘特征、纹理特征等。越往后，特征的组合信息越明显，抽象的层次更高。到最后输出的时候，我们得到的是最高层次的抽象信息，也就是“这张图是哪个数字”这样的信息。我们完成了从底层像素信息到顶层抽象信息的转化。
那既然我们在传统图像领域已经有很多先验的信息，可以用这些先验来初始化卷积核从而加速训练过程吗？理论上对于底层的特征提取，利用一些先验的卷积核，比如边缘检测、纹理检测，能够加快收敛。在数据量较小的任务，或者与先验知识高度重合的任务中，可以这么做。但在复杂的任务中，如果数据量足够的情况下，随机初始化通常更灵活，能让神经网络自动学习到更加抽象的特征。

2.3 池化层

在一个卷积神经网络中，通常还有池化层的概念。如图：

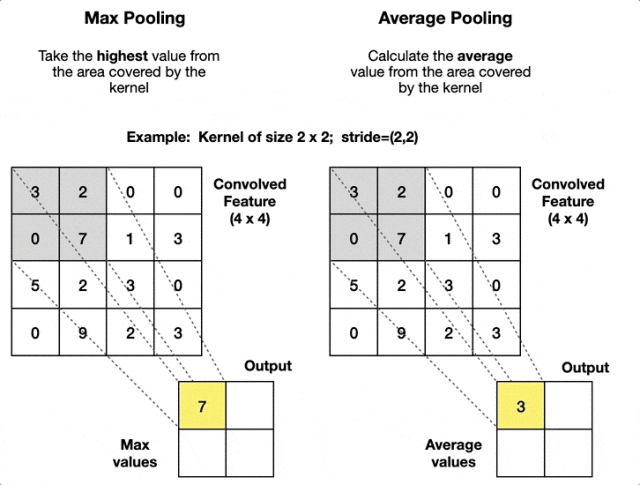
池化层是采用池化窗口，对特征图进行下采样，图中分别是最大池化（Max Pooling）和平均池化（Average Pooling）。

• 最大池化：取池化窗口中的最大值，能够保留最显著的特征。
• 平均池化：取池化窗口中的平均值，适用于平滑特征。

熟悉数据处理的朋友应该知道下采样的概念，它能够帮助我们减少运算量，保留相对重要的特征信息。举个例子，一张4096X4096像素的数字3的图片，我们把它下采样到32X32像素的图片。如果我们人眼依然能够分辨这是一张数字“3”，那么理论上这张32X32的图片中提供的的特征信息依然足够让我们的神经网络对它做出正确分类。

3. 卷积网络反向传播

卷积运算是如何进行反向传播的？我们通过一个实际的例子来直观的感受一下，假设输入图像X，卷积核W，输出图像Y：

\[X\ast W=Y \]

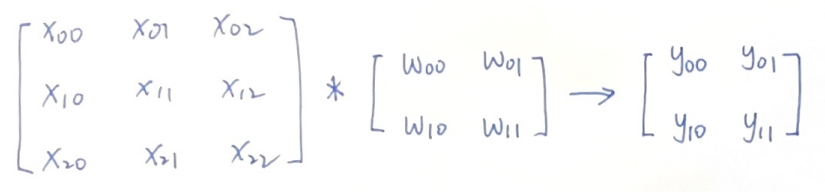
现在我们的损失函数L反向传播到Y，已知\(\partial L/\partial Y\)，希望得到\(\partial L/\partial X\)和\(\partial L/\partial W\)

为了更清晰的展示计算过程，我们把卷积运算计算过程直接写出来：

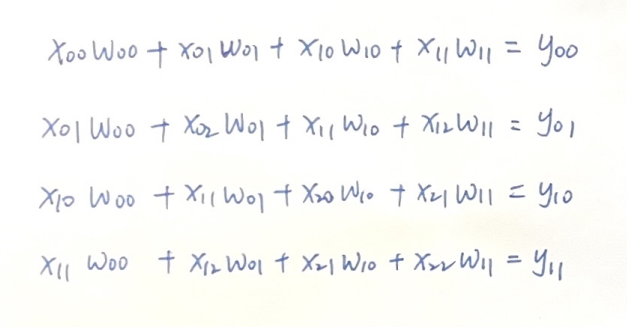
3.1 对X的导数 \(\partial L/\partial X\)

我们先看比较通常的情况，也就是图像X的中间区域，因为中间区域参与了4次卷积运算，我们对\(x_{11}\)的导数做如下推导：

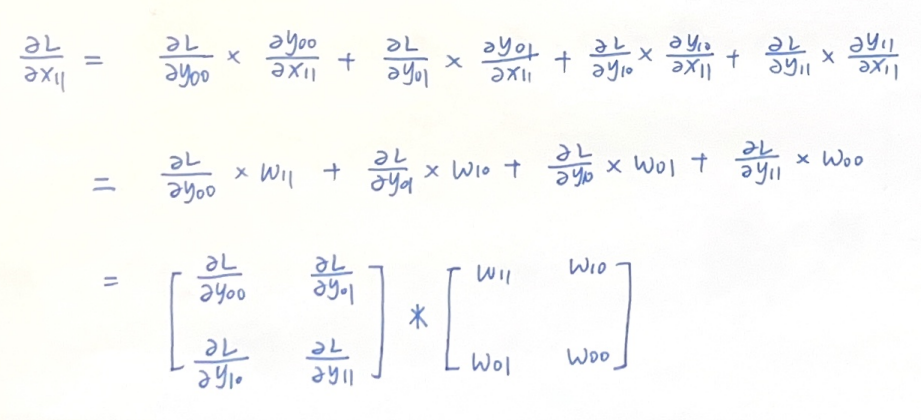
可以看到后面这一项刚好是W矩阵旋转180度的结果。
我们再看两个图像边缘部分的特殊案例，看看能否得到什么结论：

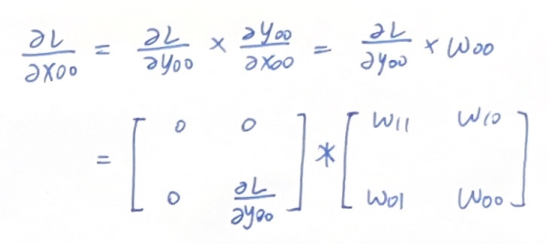
后面这一项我们都写成了W矩阵旋转180度，我们记作\(W_{rot180}\)
对于前面这一项，我们只要稍加变化，就能轻易看出规律。前面这一项似乎也是个滑动窗口，只不过在边缘处滑出了\(\partial L/\partial Y\)矩阵。
因此我们把\(\partial L/\partial Y\)这个矩阵周围补上一圈0，然后和\(W_{rot180}\)做卷积运算，结果刚好是\(\partial L/\partial X\) ！

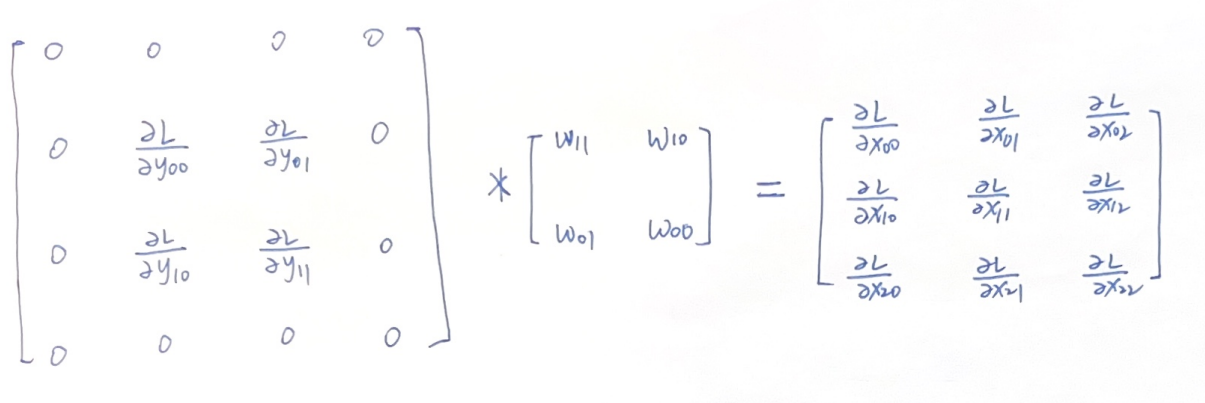
3.2 对W的导数 \(\partial L/\partial W\)

类似的，我们把对W的导数也表达出来，这里计算了\(W_{00}\)和\(W_{01}\)

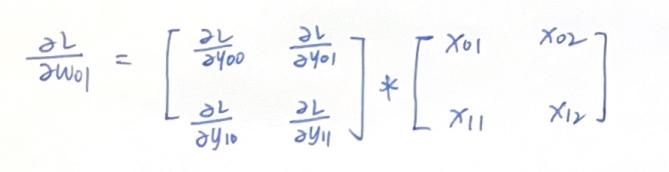
感兴趣的话可以把对W的元素的导数都写出来，观察可见，这次似乎后面这项是在X上的滑动的窗口，由此我们可以写出：

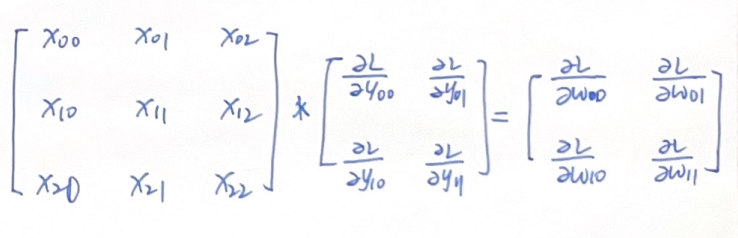
也就得到了\(\partial L/\partial W\)

3.3 池化层的反向传播

池化层的连接关系更加简单，因此反向传播的计算也很简洁。

最大池化：
前向传播时记录最大值位置。例如，输入\(\begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix}\)，最大池化输出为4。反向传播时，梯度仅传递到最大值位置：若δY=0.5，则\(δX=\begin{bmatrix} 0.5 & 0 \\ 0 & 0 \end{bmatrix}\)

平均池化:
梯度均匀分配到所有输入位置。例如，输入同上，平均池化输出为(4+2+1+3)/4=2.5。反向传播时，\(δX=\begin{bmatrix} 0.125 & 0.125 \\ 0.125 & 0.125 \end{bmatrix}\)（假设δY=0.5）

来源链接：https://www.cnblogs.com/wangle1006/p/18758300