当神经网络的层数增加，结构变复杂后，如果只用纯python（再加Numpy）来实现，代码将变得异常复杂，且难以阅读和调试。此时，就需要引入一些著名的深度学习框架了，比如PyTorch, TensorFlow等。
运用这些框架，你往往只需要定义一个神经网络的架构，反向传播过程则是自动完成的，你无需手动的去实现这部分繁琐的链式求导过程。这个自动求导的机制，就叫做自动微分（Automatic Differentiation）。自动微分是PyTorch等框架提供的重要功能。
自动微分是如何实现的？从程序设计的角度看，这是一个很有趣的问题，本篇文章我尝试用一些较为简洁的例子来研究这种自动化实现的方法。

一个简单的例子

我们先看一个极简的计算流程：

a = 2
b = a * 3    
c = a + 2
d = b + 4
e = c * d

用一个计算图（Computational Graph）去表达这样一个计算过程：

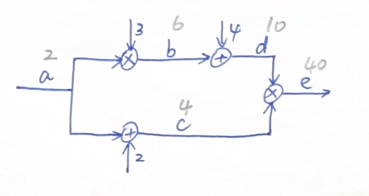
图中，当输入a = 2时，各个变量通过一系列的依次计算，最终得到e = 40，图中已标出各变量值（计算非常简单），这一过程，就相当于我们前文中讨论过的前向传播过程。
现在，我们希望计算最终结果e关于各个变量（a，b，c，d）的导数，由于都是简单的加法乘法运算，这一过程也比较简单，我们从后向前依次对各变量导数进行计算：

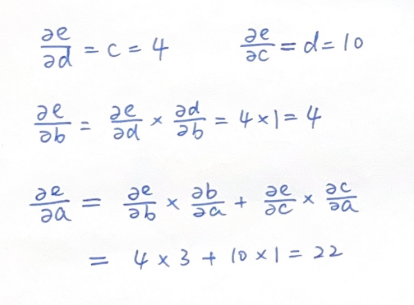
这一过程，就相当于我们前文中讨论过的反向传播过程，也就是运用链式法则，从后向前依次计算梯度的过程。
输入数据从前向后经过计算图网络得到最终结果，这个过程就像是水经过管道系统缓缓流动到出水口一样，这也就是框架TensorFlow中，flow一词的来源。

那么Tensor是什么概念呢？从上面的描述中，我们可以推测它应该是某种在计算网络中流动的“数据”的表示。我们再来看上述前向传播和反向传播过程。

计算流程的框架构建

当数据经过前向传播得到结果后，计算图的结构实际上已经确定了下来，此时，所有的求导所需信息（变量是多少，变量是怎么计算得到的）都应该已经确定了，不需要我们再提供其他额外信息。因此，反向求导过程自然可以用自动化的方式进行。而不用向上述一样手动计算。

为了构建这一“自动化”过程，我们需要在前向传播时，运用某种机制去记录下整个计算流程。观察上述计算图，这是一个典型的有向图结构。在这个图结构中的数据对象（比如b，c，d，e），如果它们不仅包含自己的值，还知道它们自己是通过哪些数据对象经过什么样的计算得到的，这样的话，有向图结构的信息就保存下来了。也就是整个计算流程就记录下来了。

为此，我们需要扩展各个数据对象的定义，它们不仅要记录本身的值，还要记录这个值是如何得到的。具体来说，它们的数据结构中应该包含如下信息：

数据值，这个是变量本身的值
导数（梯度），反向传播时各个变量的梯度数据，上文中我们计算了最终输出e关于所有变量（a、b、c、d）的导数
该数据是通过何种运算得到的，上文中，b是通过求积运算得到，c是通过求和运算得到
该数据是通过哪些其他数据得到的，上文中，b是通过a和3得到，e是通过c和d得到

明确了数据对象的扩展定义，我们在前向传播时，通过重写表达式中的运算符，就能将各个数据“链接”起来，形成计算图。这个扩展的数据结构（包含数据值，梯度值，以及它是如何运算得到的），就是深度学习框架中Tensor的概念。

是时候上代码了，我们把上述的信息用一个Tensor类来承载，其代码结构如下：

class Tensor(object):
    def __init__(self, data,creators=None, creation_op=None):
        self.data = data
        self.grad = None
        self.creation_op = creation_op 
        self.creators = creators 
        
    def __add__(self, other):
        return Tensor(self.data+other.data,
                     creators=[self,other],
                     creation_op="add")
        
    def __mul__(self, other):
        return Tensor(self.data*other.data,
                     creators=[self,other],
                     creation_op="mul")
        
    def __str__(self):
        return str("data: "+self.data.__str__()+"\n"
                   +"grad: "+self.grad.__str__()+"\n"
                   +"creation_op: "+self.creation_op)

我们用这个类再去写计算流程：

a = Tensor(2)
b = a * Tensor(3)    
c = a + Tensor(2)
d = b + Tensor(4)
e = c * d

print(e)
print(e.creators[0])
print(e.creators[1])
print(e.creation_op)

运行结果：

40
4
10
mul

从运行结果可以看到，输出e的结果为40，与之前我们的计算相符，它是由两个数4和10通过运算“mul”得到的。

至此，我们通过构建前向传播计算过程，得到了运算结果，并且将计算过程通过计算图保存了下来。这里我们注意到所有的Tensor中的grad还都是None。下一步，我们就要借助这个计算图，对所有变量进行梯度计算。

自动求导的思路

我们从e这个数据看，e是输出，我们希望找到的是它关于其他变量的导数，e关于自己的导数是1，所以e的grad为1。这是梯度计算的起点。
在e这个Tensor中，我们可以知道e是通过d和c相乘得到，因此，e关于d和c的导数可以轻易得到，分别为c和d的值，也就是4和10，e将它们分别传递给d和c这两个Tensor。
在d这个Tensor中，它从Tensor e那里接收到了\(∂e/∂d\)，将其赋值给自身的grad变量，并且它还知道自己是通过Tensor b，和一个Tensor 4相加得到，通过链式法则他把自己的grad，也就是\(∂e/∂d\)，乘以\(∂d/∂b\)，得到\(∂e/∂b\)，并把它传递给Tensor b。同理，也将梯度传递给Tensor 4，但由于Tensor 4是个常量，我们无需关心他的梯度。
同样的，Tensor c从Tensor e那里接收到\(∂e/∂c\)，赋值自身的grad后，将其乘以\(∂c/∂a\)，得到\(∂e/∂a\)，传递给Tensor a。

从上述描述中，我们可以抽象出一般规律，也就是反向传播过程中，每个Tensor都是接收到上一个Tensor传递过来的导数，对自身grad赋值，然后通过自己保存的creators信息（也就是该Tensor是通过哪些Tensors经过什么计算得到的），用链式法则为自己的creators计算梯度并传递给它们。我们用代码示意这一过程：

    def backward(self, grad=-1): 
        if(grad==-1):
            self.grad = 1
        else:
            self.grad = grad  #注意！这里还需修改
        
        if(self.creation_op == "add"): 
            self.creators[0].backward(self.grad) 
            self.creators[1].backward(self.grad)  
        
        if(self.creation_op == "mul"): 
            self.creators[0].backward(self.grad*self.creators[1].data) 
            self.creators[1].backward(self.grad*self.creators[0].data)

这里我们用grad=-1这个默认入参来区别梯度计算的起点，也就是e的grad设置为1。

对于重复使用的变量

当我们继续往下进行梯度计算时，会发现一个问题，对于输入Tensor a来说，有两条路径都可以将梯度传递给a：一条是由Tensor c中，计算\(∂e/∂c\)乘以\(∂c/∂a\)，得到\(∂e/∂a\)；另一条是在Tensor b中，\(∂e/∂b\)乘以\(∂b/∂a\)得到\(∂e/∂a\)。如果使用上述代码，a的grad将被其中一个覆盖掉。

从我们之前手算的过程来看，\(∂e/∂a\)应当是两条路径上梯度之和，也就是\(∂e/∂a=∂e/∂c*∂c/∂a+∂e/∂b*∂b/∂a\) 这也是符合链式法则原理的。对于重复使用的Tensor，它的梯度应为所有反向路径上传递到它的梯度之和。

因此，我们的Tensor类应改为：

class Tensor(object):
    def __init__(self, data,creators=None, creation_op=None):
        self.data = data
        self.grad = None
        self.creation_op = creation_op 
        self.creators = creators 

    def backward(self, grad=-1): 
        if(grad==-1):
            self.grad = 1
        else:
            if (self.grad is None):
                self.grad = grad
            else:
                self.grad+=grad
        
        if(self.creation_op == "add"): 
            self.creators[0].backward(self.grad) 
            self.creators[1].backward(self.grad)  
        
        if(self.creation_op == "mul"): 
            self.creators[0].backward(self.grad*self.creators[1].data) 
            self.creators[1].backward(self.grad*self.creators[0].data)
        
    def __add__(self, other):
        return Tensor(self.data+other.data,
                     creators=[self,other],
                     creation_op="add")
        
    def __mul__(self, other):
        return Tensor(self.data*other.data,
                     creators=[self,other],
                     creation_op="mul")
        
    def __str__(self):
        return str(self.data.__str__())

我们验证一下结果：

a = Tensor(2)
b = a * Tensor(3)    
c = a + Tensor(2)
d = b + Tensor(4)
e = c * d

e.backward()

print(a.grad)

得到：

与我们的手算结果相符。

真实框架中的Tensor——多维数据的容器

在上述的讨论中，我们的Tensor中只包含一个标量，事实上，在深度学习框架中，Tensor（张量）是核心数据结构，它可以包含不同维度的数据。

标量（0维张量）：单个数值，如 5
向量（1维张量）：一维数组，如 [1, 2, 3]
矩阵（2维张量）：二维表格，如 [[1,2], [3,4]]
高阶张量（3维及以上）：例如图像数据可表示为 [batch_size, 高度, 宽度, 通道数]

它类似于Numpy的ndarray，我们现在用ndarray来代替原来的标量数据，看看代码有什么变化：

import numpy as np

class Tensor(object):
    def __init__(self, data,creators=None, creation_op=None):
        self.data = np.array(data)
        self.grad = None
        self.creation_op = creation_op 
        self.creators = creators 

    def backward(self, grad=None): 
        if(grad is None):
            self.grad = Tensor(np.ones_like(self.data))
        else:
            if (self.grad is None):
                self.grad = grad
            else:
                self.grad+=grad
        
        if(self.creation_op == "add"): 
            self.creators[0].backward(self.grad) 
            self.creators[1].backward(self.grad)  
        
        if(self.creation_op == "sub"):
            self.creators[0].backward(Tensor(self.grad.data), self)
            self.creators[1].backward(Tensor(self.grad.__neg__().data), self)

        if(self.creation_op == "mul"): 
            self.creators[0].backward(self.grad*self.creators[1]) 
            self.creators[1].backward(self.grad*self.creators[0])                  
                    
        if(self.creation_op == "mm"):
            c0 = self.creators[0]
            c1 = self.creators[1]
            new = self.grad.mm(c1.transpose())
            c0.backward(new)
            new = self.grad.transpose().mm(c0).transpose()
            c1.backward(new)
        
    def __add__(self, other):
        return Tensor(self.data+other.data,
                     creators=[self,other],
                     creation_op="add")
        
    
    def __sub__(self, other):
        return Tensor(self.data - other.data,
                      creators=[self,other],
                      creation_op="sub")
        
    def __mul__(self, other):
        return Tensor(self.data*other.data,
                     creators=[self,other],
                     creation_op="mul")

    def mm(self, x):
        return Tensor(self.data.dot(x.data),
                      creators=[self,x],
                      creation_op="mm")
        
    def __str__(self):
        return str(self.data.__str__())

代码中有如下变化：

将数据data作为ndarray处理，将梯度grad作为Tensor处理
添加了减法和向量矩阵乘法支持，其中向量矩阵乘法在神经网络中运用频繁
对反向传播起点的梯度，采用和其维度一致的全1矩阵代替

我们验证其对矩阵乘法的求导可行性：

a = Tensor([2, 2, 3])
b = Tensor([2, 3, 4]) 
c = Tensor([[1,2,3],[2,3,4],[3,4,5]])

d = a * c
print(d)

d.backward(Tensor(np.array([1,1,1])))
print(a.grad.data)
print(c.grad.data)

结果：

[[ 2  4  9]
 [ 4  6 12]
 [ 6  8 15]]
[[1 2 3]
 [2 3 4]
 [3 4 5]]
[2 2 3]

来源链接：https://www.cnblogs.com/wangle1006/p/18749130

本站所有资源来自于网络，仅供学习与参考，请勿用于商业用途，否则产生的一切后果将由您(转载者)自己承担！
如有侵犯您的版权，请及时联系3500663466#qq.com(#换@)，我们将第一时间删除本站数据。

THE END

Java 后端开发编程开发