Transformer 笔记 (CS224N-7)

模型回顾

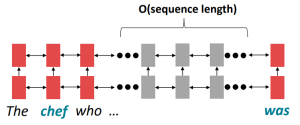
问题：RNN需要经过k步才能对远距离的单词进行交互，例如

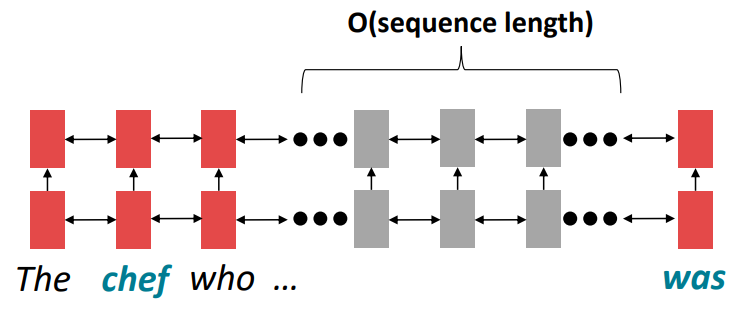
这里的was是chef的谓语，二者的关系十分紧密，但是使用线性顺序分析句子会导致如果was和chef的距离较远，它们会难以交互（因为梯度问题）

Self Attention

键值对注意力

(1)我们可以将注意力视为在键值存储中执行模糊查找，在一个key-value查找表中，查询会对所有keys进行软匹配，然后相应的value将乘以权重并求和

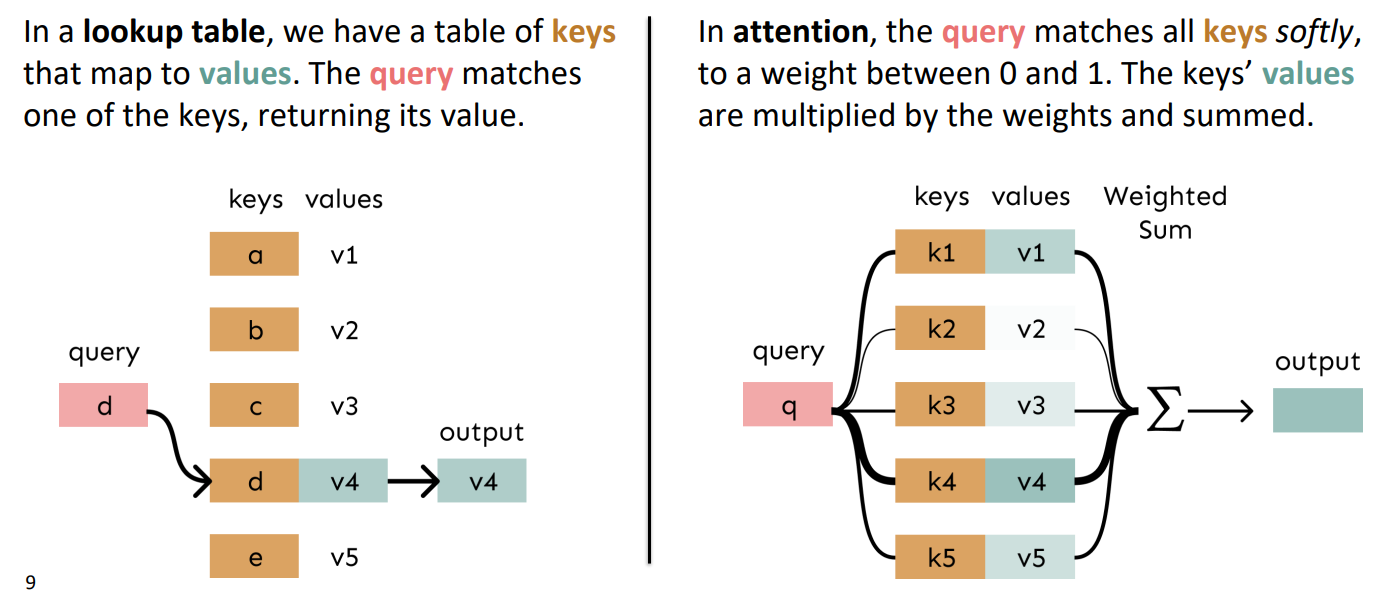
(左边是强匹配，右边是软匹配)

(2)理解

①键值对Attention最核心的公式如下$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}}V)$$

如果这个公式很难理解，那么我们先从self-attention的原始形态入手，原始形态为 \(softmax(XX^T)X\)

②下面解读这个原始形态的公式：
\(XX^T\) 是输入矩阵\(X\)中每一个词向量与自己的内积，我们已经知道向量的内积表示向量的相关性，所以\(XX^T\)相当于一个类共现矩阵，再用softmax归一化成权重，那么便得到了一个输入矩阵\(X\)的相关度矩阵，可以将其理解为一个键值对表。将这个键值对表再\(X\)乘积，就实现了软匹配键值对表注意力

③接下来解释一下 \(softmax(\frac{QK^T}{\sqrt{d_k}}V)\) ：

\(Q,K,V\) 是什么？ \(XW^Q=Q,XW^K=K,XW^V=V\) ，可以看到它们其实就是调整后的\(X\)，为什么我们不直接使用\(X\)，因为调整矩阵\(W\)是可以训练的，起到一个缓冲的效果

\(\sqrt{d_k}\) 的意义在于，假设 \(Q,K\) 里的元素的均值为0，方差为1，那么 \(A^T=Q^TK\) 中元素的均值为0，方差为d。当d变得很大时，\(A\)中的元素的方差也会变得很大，如果\(A\)中的元素方差很大，那么 \(softmax(A)\) 的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。因此\(A\)中每一个元素除以 \(\sqrt{d_k}\) 后，方差又变为1。这使得 \(softmax(A)\) 的分布“陡峭”程度与d解耦，从而使得训练过程中梯度值保持稳定（详见后续 缩放点积）

(3)问题与解决

①如何加入考虑序列顺序：由于自我注意不是建立在有序信息中的，我们需要在键、查询和值中对句子的顺序进行编码

我们将每个序列索引表示为向量\(p_i\)，然后将位置向量添加到我们的输入中 \(\widetilde x_i=x_i+p_i\)

• 正弦曲线的位置向量：连接不同周期的正弦函数成为向量
  (随着周期开始可以推断出更长的序列，但是不能学习，不能外推)
• 从头学习的位置向量：学习一个矩阵\(p\)，让每一个位置向量\(p_i\)为该矩阵的一列
  (具有灵活性，每个位置都需要学习以适应数据，绝对不能外推到输入序列以外，大多数系统都使用此方法)

②如何加入非线性（self-attention深度学习的输出结果是线性的，只是加权平均数）

在自注意力机制中加入非线性：添加一个前馈网络来对每个输出向量进行后处理（可以提供更多的非线性和学习能力）

\[m_i=MLP(output_i)=W_2*ReLU(W_1output_i+b_1)+b_2 \]

③如何防止窥探未来（Attention Mask）：（因为Transformer在训练时是不应该提前看到后面的信息的，这属于作弊，作弊会导致用“你好世界上的人”训练出来的模型在输入“你好”时可能不会生成“世界上的人 ”）通过将注意力得分设置为 \(-\infty\) 来掩盖对未来单词的注意力

(5)总结：self-attention需要位置表示、非线性和掩蔽未来

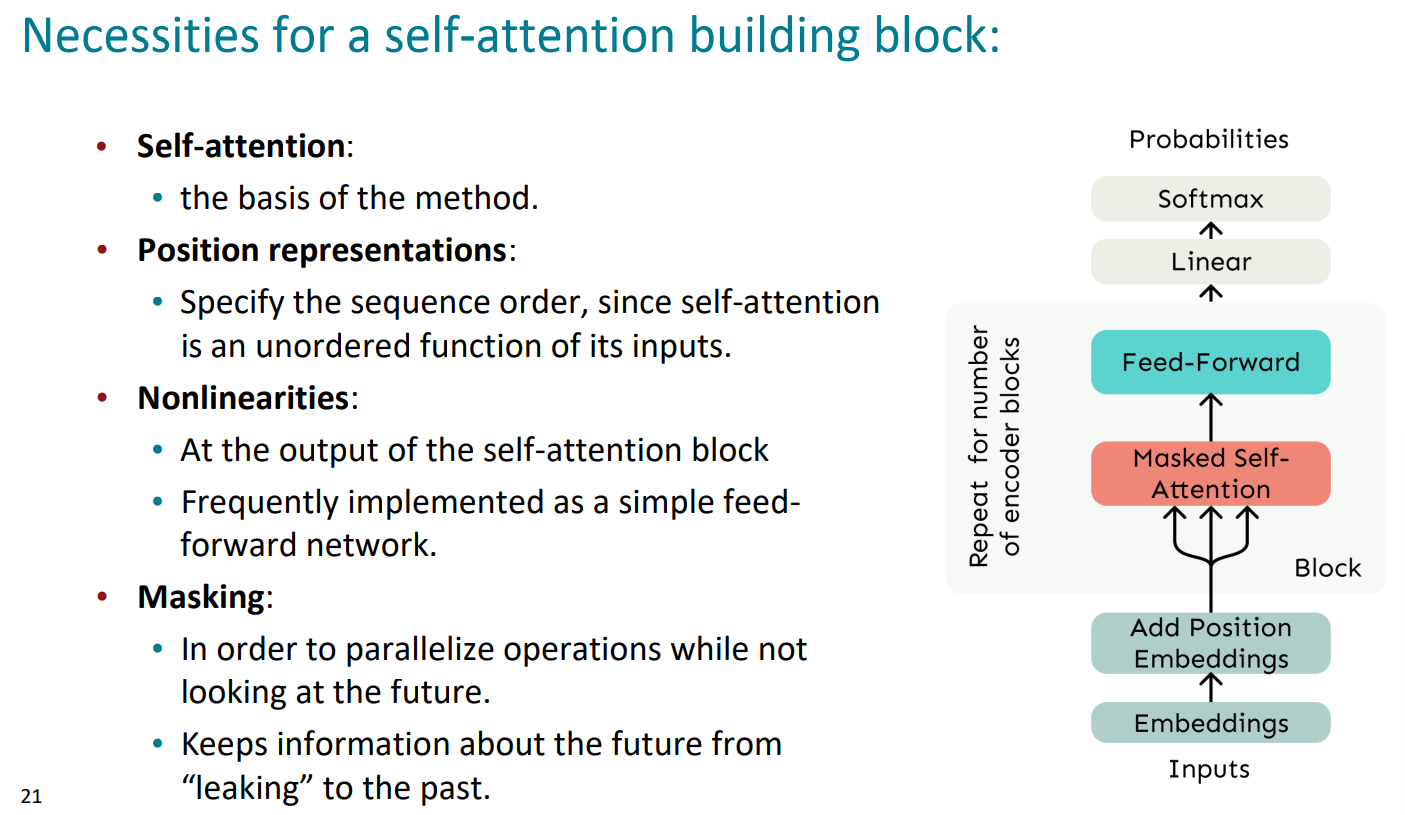
右边的流程图即为self-attention的全过程

Transformer模型

Multi-head Self Attention

(1)为什么要使用multi-head self-attention

模型在对当前位置的信息进行编码时，会过度的将注意力集中于自身的位置（虽然这符合常识）而可能忽略了其它位置，因为当文本很长时，自身的权重过高会导致分配给其他位置的权重较小，可能会存在某些位置权重矩接近于0的情况（即被忽略），这是我们不想看到的

(2)主要思路

让我们回忆一下这个公式

\[output_l=softmax(XQ_lK_l^TX^T)XV_l \]

我们将通过多个Q、K、V矩阵定义多个注意力头 ，每个注意力头都独立的进行注意力感应，这里我们定义 \(Q_l,K_l,V_l \in R^{d \times\frac{d}{h}}\) （ \(R^{m\times n}\) 表示一个\(m \times n\)的矩阵，h是注意力头的数量，\(l\)的范围从1到h）

最后再将h个输出结果合并，即可得到一个\(d\times d\)的输出矩阵

Scaled Dot Product

(1)为什么要使用点积缩放

当维数d变得很大时，向量的点积往往会变得非常大，所以我们需要将attention scores除以注意力头的数量，即d/h

\[output_l=softmax(\frac{XQ_lK_l^TX^T}{\sqrt{d/h}})XV_l \]

Encoder-Decoder

(1)残差连接和层规一化，通常被一起作为”Add & Norm”

(2)残差连接（即残差网络思想）：可以帮助模型训练的更好

(3)层规一化：可以帮助模型训练的更快

通过归一化，减少隐藏向量值的无信息变化，我们得到

(5)The Transformer Decoder

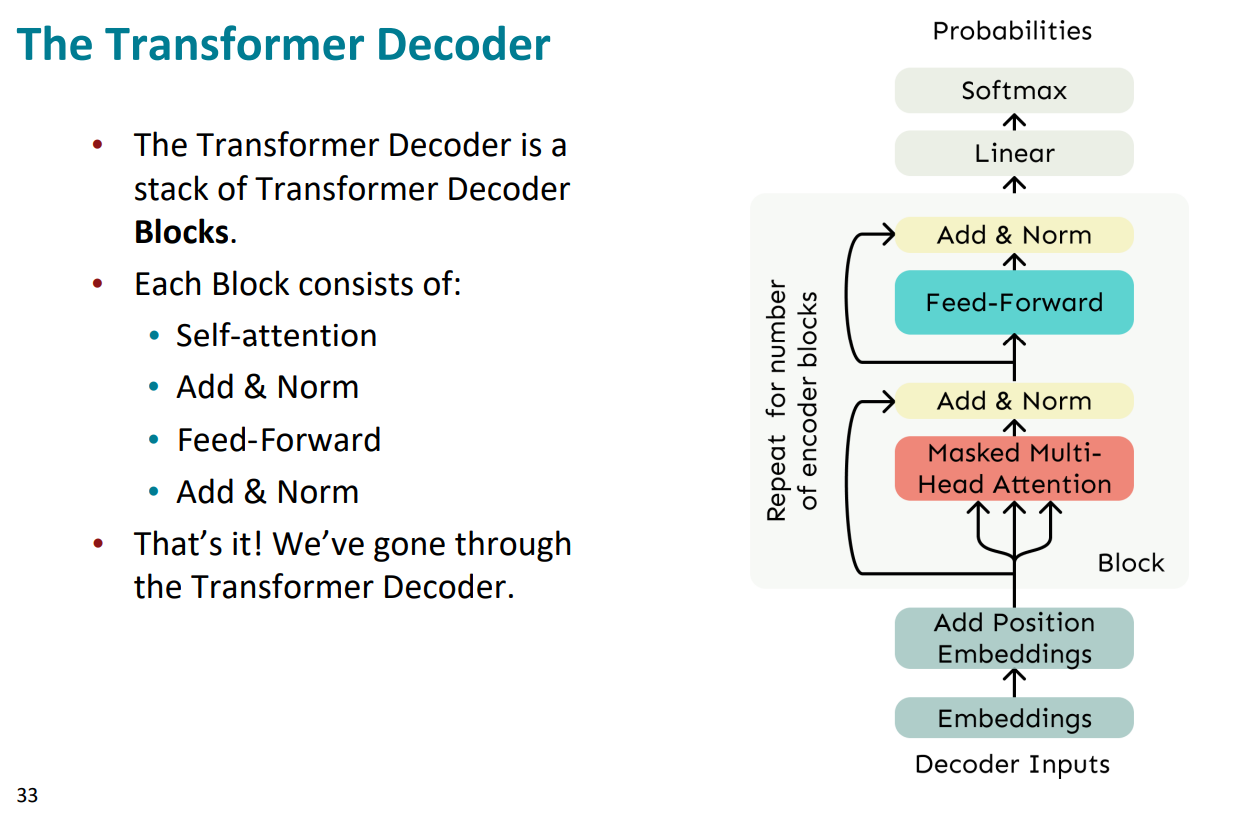
• Transformer解码器由一堆Transformer解码器块组成
• 每个解码器块包括:
  ①self-attention
  ②add&norm
  ③feed-forward
  ④add&norm

(6)The Transformer Encoder

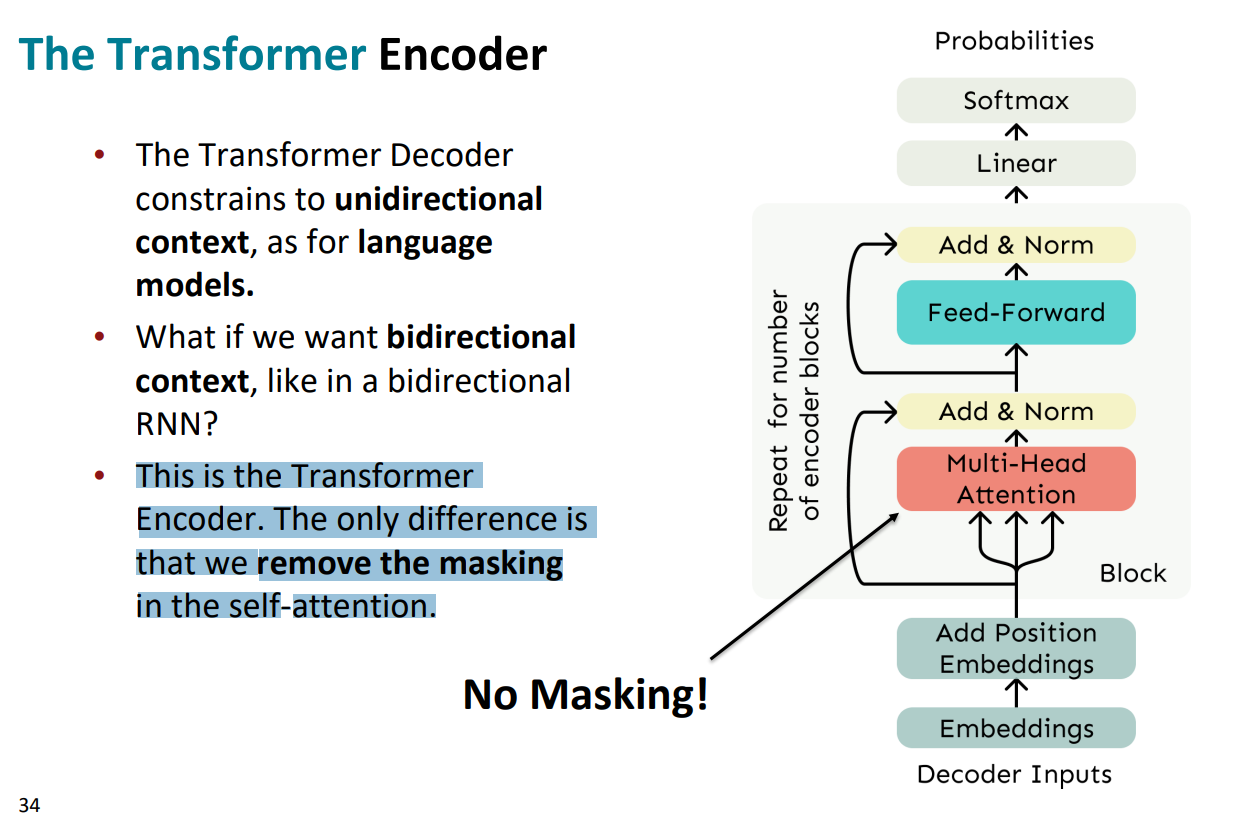
与解码器不同的是，编码器将去除了self-attention中的mask机制

(7)总结

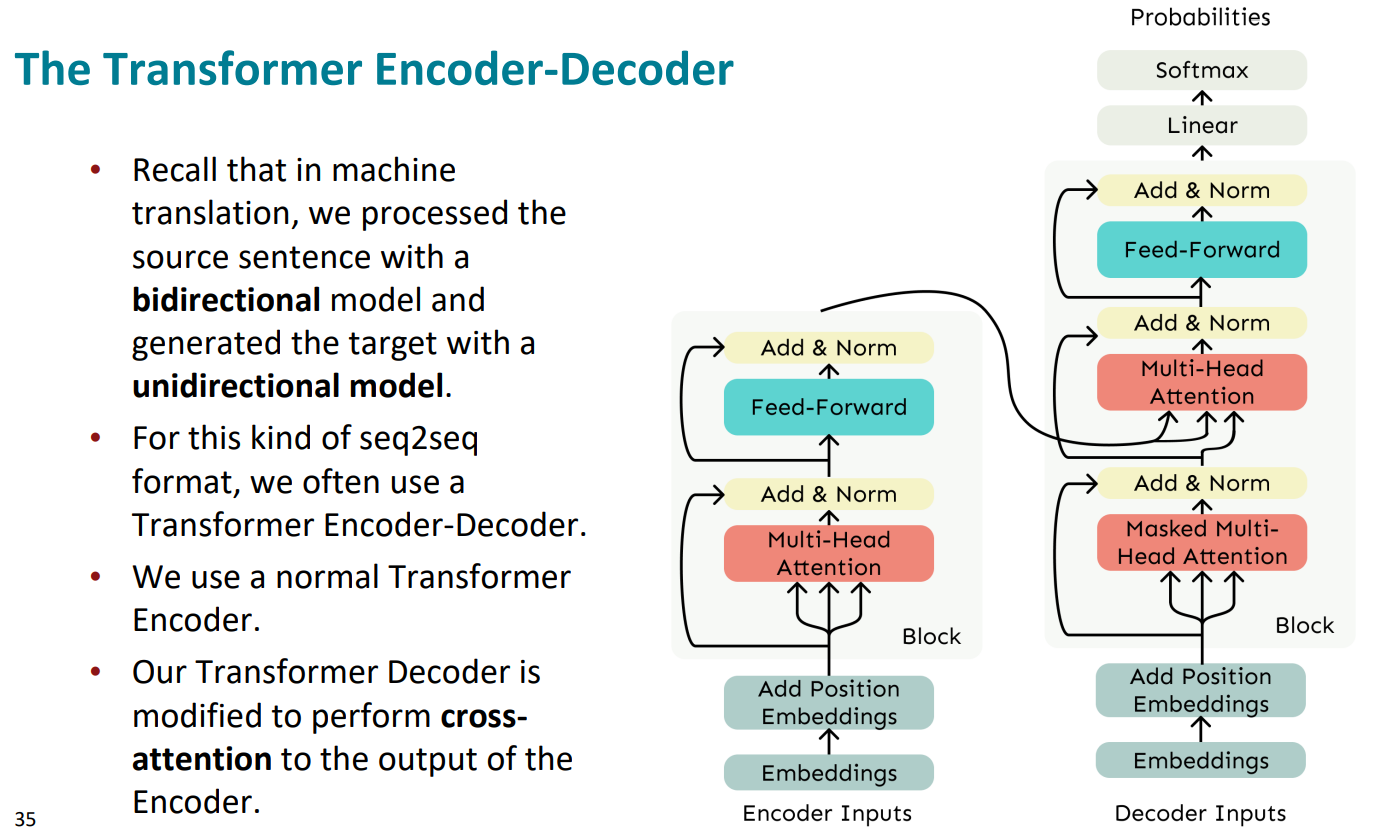
回顾一下，在机器翻译中我们用双向模型处理源句子，并用单向模型生成目标。在Transformer中的解码器中，我们可以进行修改，对编码器的输出进行交叉关注，于是便得到了右侧的模型（是我们Transformer的完整模型）

模型中左边为编码器，右边为解码器，解码器中第一个Masked Multi-Head Attention是直接根据输入的X矩阵的到Q、K、V，而第二个Multi-Head Attention是根据编码器的输出得到K、V，但Q仍然是由编码器的输出得到

缺点与问题

(1)自我关注的二次运算会导致计算的增长 \(O(n^2d)\)

• 相关研究：Linformer
  关键思想：将序列长度维度映射到值、键的低维空间

(2)简单的绝对指数使我们能做的做好的表示位置的指数吗

推荐一篇很通俗易懂的讲解https://blog.csdn.net/Tink1995/article/details/105080033

来源链接：https://www.cnblogs.com/mianmaner/p/18760052