#PosFormer
本文简要介绍被ECCV 2024录用的论文PosFormer: Recognizing Complex Handwritten Mathematical Expressions with Position Forest Transformer,上交推出 PosFormer!优化位置识别任务来辅助表达式识别,复杂公式识别能力再创新SOTA!
- 论文地址:https://arxiv.org/abs/2407.07764
- 代码地址:https://github.com/SJTU-DeepVisionLab/PosFormer
1. 引言
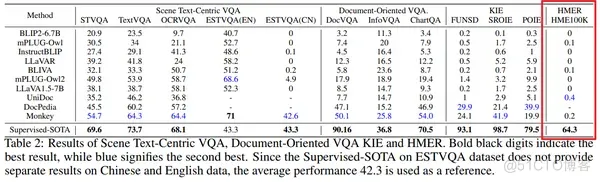
手写数学表达式作为语言和符号之间的桥梁,在数学、物理和化学等领域中很常见。相应的任务,即手写数学表达式识别(HMER),旨在准确地将表达式图像转换为 LaTeX 序列。这个任务在在线教育、手稿数字化和自动评分等人机交互场景中有广泛应用。近期,我们注意到多模态大语言模型在文本图像领域具有泛化性高的性能,但是大多数大模型在手写数学表达式识别上还不够理想参考MultimodalOCR,如下图红框所示:
这说明当前识别手写数学表达式仍比较困难,具体地,其主要面临着两大挑战:符号间关系的复杂性[1]和手写输入的多样性。
传统方法通常涉及两步流程:识别单个符号并随后根据语法规则进行校正。近年来,随着深度学习的发展,开发了两种主流方法以提高识别性能:基于树的方法和基于序列的方法。
具体来说,基于树的方法遵循 LaTeX 的语法规则,将每个数学表达式建模为树结构[2][3],然后输出基于语法树的完整三元组(父节点、子节点、父子关系)的序列,并将其解码为 LaTeX 序列。这些方法由于表达式中树结构的多样性不足,表现出较低的准确性和较差的泛化能力。基于序列的方法将 HMER 建模为端到端的图像到序列任务[4]。
- 方法(PosFormer)
如图1所示,位置森林变换器(PosFormer)由 DenseNet[5]、位置森林和表达式识别头组成。
首先,DenseNet从输入图像中提取二维视觉特征。这些特征随后被送入基于注意力的Transformer解码器以获取具有辨别力的符号特征。
然后使用并行线性头来识别 LaTeX 表达式。为了促进位置感知的符号级特征表示学习,在表达式识别的同时引入位置森林进行联合优化。
具体来说,这个过程首先将数学表达式的序列编码为标识符集,每个标识符是一个表示其位置信息的字符串。然后使用两个位置森林头分别解析其嵌套层次和相对位置。
2.1 Position Forest
根据 LaTeX 的语法规则,表达式可以分为多个独立或嵌套的子结构,如图2所示,包括上标-下标结构、分数结构、根式结构和特殊运算符结构。在每个子结构内,符号的相对位置关系根据其在图像中的空间位置分为三类:上、下和中。利用这一先验知识,我们将 LaTeX 数学表达式建模为位置森林结构。其构建遵循以下三条规则:
- 这些子结构按从左到右的顺序进行编码;
- 每个子结构根据符号之间的相对位置编码成树,其主体为根节点,上部为左节点,下部为右节点;
- 根据子结构的关系,这些编码的树按顺序或嵌套排列形成位置森林结构。
然后依照上面的规则,我们的编码过程如图3所示,每个符号在森林中被分配一个位置标识符以表示其相对空间位置。对于给定的一个公式图像 ,其对应的标识符集合 被定义为 。H、W、T分别为图像高度、图像宽度、序列长度。例如图3中的 ” 2 ” 对应的标识符为: ” “。
考虑到这些标识符的长度不同,我们将标识符填充组织成矩阵,其中每个向量通过非线性层转换为标识符嵌入,最后将符号顺序的绝对位置编码添加到标识符嵌入中。生成公式如下:
这些嵌入向量 和主干网络提取的视觉特征 (其中 )被输入到基于 Transformer 的三层解码器块中。这些块主要由多头注意力 (MHA) 、隐式注意力校正(IAC,稍后介绍)和前馈网络(FFN)组成,处理这些输入以产生输出特征 ,用于预测表达式识别 (常规分支) 和位置识别(我们设计的分支)。
接着,我们将位置识别任务分为两个子任务:嵌套层级预测任务 和 相对位置预测任务。首先,给定标识符集合 ,我们需要构造其嵌暮层级和相对位置的ground truth。
对于第 个标识符 为标识符长度,可以很容易地确定其嵌套层级为 ,相对位置为 。例如,在分析标识符 MLLR 时,可以推断该符号位于包含三个嵌套级别的子结构中,其相对位置位于最后一个嵌宏子结构的下部 R 。
基于此,嵌套层级的ground truth被构造:
表示嵌套级别的最大数量。相对位置的ground truth被构造:
最终,在解码步骤 ,取 ,预测当前步骤嵌套层级和相对位置为:
2.2 Implicit Attention Correction
如图4所示, 我们将一些LaTeX 符号定义为结构符号:在图像中没有实体,用于描述实体符号之间的位置和层次关系。
在解码结构符号时,覆盖问题(即过度解析和欠解析)限制了识别能力。为了解决这些问题,CoMER[6] 通过减去所有前一步的注意力来细化当前解码步骤的注意力权重。然而,在解码一些结构符号时,我们观察到模型将注意力分配到尚未解析的区域,甚至是整个图像。
在减法操作之后,这种机制会导致依赖于过去对齐信息的后续解码步骤中校正注意力的不准确性。为此,我们提出了一种简单而有效的校正解决方案,通过引入零注意力作为我们的校正项。具体来说,当一个实体符号被解码时,我们将与前面的结构符号相关的注意力权重重置为零。
这很容易解释:当我们鼓励模型对解码实体符号产生精确的注意力时,只要从已经解析的实体符号中减去这些注意力权重就可以了,因为数学表达式图像上只存在实体符号。
因此,注意力校正过程如下:
设 为第 层解码器产生的注意权重(实验中为 ), 表示这些结构符号的集合,我们提出一个指示函数 来引入相应的修正项 ,
表示Hadamard积, 表示沿通道的拼接操作。
2.3 Loss Function
最终模型在多任务设置下进行端到端川练,其目标是:
其中 表示groundtruth LaTeX序列, 为groundtruth嵌套层级, 表示 groundtruth相对位置。 分别表示三个任务的预测分布。最后,整体的训练损失总结为:
最后,整体的训练损失总结为:
- Experimental Results
首先,我们在单行数据集CROHME上进行实验。具体来说,为了公平比较,我们提供了 PosFormer 有和没有数据增强的性能结果。我们强调,一些先前的先进方法使用的数据增强方法没有开源,因此我们只在都没有数据增强的情况下与这些方法进行对比。
其次,我们还在大规模单行数据集HME100k上进行了实验,这里的对比都没有使用数据增强。
与单行数据集相比,多行手写数学表达式数据集M2E包含更多的复杂结构和长序列图像。为了证明我们模型的有效性和鲁棒性,我们在该数据集上与之前的最先进方法进行了比较。
我们进行消融实验,展示了PosFormer 的两个组件——位置森林(PF)和隐式注意力校正(IAC)带来的性能提升。
位置森林(PF)可以很容易地封装成一个插件组件。为了证明其鲁棒性和通用性,我们将其扩展到基于 RNN 的方法进行了对比实验。
为了与先前的位置增强工作比较,我们在CROHME上与robustscanner[7]进行了比较。另外,引入语言模型是进一步提高性能的方向,一些 HMER 方法(例如,RLFN[8])的视觉输出被输入到语言模型[9]中,以利用语言上下文实现识别校正。尽管 PosFormer 是一种不依赖语言的模型,但它仍然实现了 6.25% 的提升。
另外,我们还构建了一个多层嵌套数据集MNE,来测试PosFormer在识别复杂嵌套表达式的能力。N1、N2和N3分别表示嵌套层数为1、2和3的子测试集。
最后,本文展示了隐式注意力校正的可视化例子:
4. Conclusions
相比主流的基于树和基于序列的方法,PosFormer提出了一种全新的角度来考虑手写数学表达式中的位置信息和嵌套关系。
本文提出了一种有效的位置森林变换器用于手写数学表达式识别,为基于序列的方法增加了位置理解组件。该方法将每个数学表达式编码为森林结构而无需额外的标注,然后解析其在森林中的嵌套层次和相对位置。
通过优化位置识别任务来辅助表达式识别,PosFormer 在复杂和嵌套的数学表达式中显式地实现了位置感知的符号级特征表示学习。开发板商城 天皓智联 TB上有视觉设备哦 支持AI相关~ 大模型相关也可用 whaosoft aiot自动驾驶也可以哦
大量实验验证了 PosFormer 的性能优越性,同时在推理过程中不会引入额外的延迟或计算成本。这凸显了在基于序列的方法中显式建模表达式位置关系的重要性,希望能带来更深远的意义和更深刻的启发。
#如何使用预训练的无条件扩散生成模型来进行条件生成的指南
预训练无条件扩散生成模型的 training-free 条件生成食谱(一)
对于扩散模型来说,可控(条件)生成和采样加速是两大热门方向,其中 CW 认为前者的可玩性和观赏性会更胜一筹,特别是研究如何利用已经训练好的无条件扩散模型来生成自己想要的图像(而不是随机生成),这点个人觉得非常好玩。于是,在调研了一些广为流传(maybe 好用)的方法之后,CW 决定把它们制成一份食谱,以便日后做(炼)菜(丹)时能够从中借鉴和调配。
既然要为日后重新调配做打算,那么就会涉及代码实现,但食谱中仅收录每种方法里关键操作的代码。另外,本食谱对于每种方法提供偏向直觉性的解释,这是考虑到厨师做菜通常不会纠结分子和原子的化学变化。对于严谨的推导和证明过程,还请各位食客自行参考论文。
注意,这份食谱所收录的方法都是 training-free 的,也就是不会对模型进行二次训练,也可称作 “sampling-based”,因为它们仅对模型的采样过程进行改造和调整。并且所用的扩散模型是无条件的,也就是没有不会有条件项作为模型输入。只要手头上有预训练的无条件扩散模型,在给出条件信息(比如参考图像、文本 prompt 等)的情况下,就能够实现可控生成。由于这种方法并没有将条件信息作为输入来进行训练,因此通常也被叫作是 “zero-shot” 和无监督的。
题外话:本文的标题有点 “Engnese” 的味道,因为其实它来自于我脑子里的 “The training-free recipe for conditional generation with pretrained unconditional diffusion models”,但纠结一番后还是想接地气一些,于是成了如今这个样子。
keywords: conditional generation, training-free, zero-shot, unsupervised, diffusion models, inverse problems, image inpainting, image restoration, image editing
图生图
这一章介绍的方法都是在给定一张参考图像的条件下进行采样生成。 在这种情况下,通常是希望模型能够生成与参考图像相似的图片,或者对参考图像进行修复(填充)和编辑等。
SDEdit
SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations 可谓是出身名门,不信你可以去看看这篇 paper 的作者们,每一位都是不得了的大佬!
但这篇论文的思路却出奇简单,或许这就是所谓的大道至简吧~
SDEdit 巧妙地利用了扩散模型采样过程所对应的 reverse SDE 的性质——采样起点可以从中间任意时刻开始。
the reverse SDE can be solved not only from , but also from any intermediate time
具体地, 先对参考图像(论文中称作 “guide”)进行加噪, 噪声强度根据扩散模型的 noise schedule 选择某个时刻 所对应的噪声强度; 然后从该时刻开始根据 reverse SDE 对加噪后的参考图像进行迭代去噪。当采样至最后时刻 , 若感觉效果不满意, 还可以将生成的结果重新加噪回 时刻, 然后再次实施同样的迭代去噪过程, 这样的玩法可以反复多次直至得到满意的效果为止。
对于一些图像编辑和修复的场景,可能我们只想要改变参考图像的某部分,让这部分就用模型采样生成的结果来代替,而另一些部分则希望保持原封不动。对于这种需求,可以在前面的基础上额外利用 mask 来指示参考图像的哪些位置是需要保持不变的,而哪些是希望用模型的生成结果来代替的(比如在 mask 中值为1的部分代表将要用模型的生成结果来覆盖)。
- SDEdit 做法的背后隐藏着什么
CW 觉得上面这幅图很好地阐释了 SDEdit 的原理:真实的图像(扩散模型学到的数据分布)和输入的参考图(上图是油画)本来隶属于不同的数据流形,经过噪声扰动后,两个流形产生了交集(扰动使得流形扩大了范围)。然后从交点开始经由扩散模型(reverse SDE)迭代去噪,从而使数据点不断向真实图像所在的流形区域移动(reverse SDE 决定了这个方向),最终将油画 project 为真实图像。
由于加噪主要破坏的是高频信息,因此在去噪后能保留住参考图的大体结构和语义(低频信息),同时又去掉了纹理等细节,从而生成的图像既能与参考图有一定相似性又显得真实(服从图像数据分布)。
- 真实度与相似性之间的 trade-off
一个需要重点考虑的问题是生成图像的真实度(realistic)与参考图像的相似性(论文中称为 “faithful”)之间的 trade-off。由上面那幅图也可以直观感受到,如果将数据点被过份地移动到真实图像的流形区域(从而远离参考图像的流形),那么虽然生成的结果显得很真实,但与参考图的相似性就难免会降低;相反,若数据点太靠近参考图所在的流形(于是离真实图像所在的流形较远),则生成的结果虽然与参考图的相似度很高,但整幅图像看起来就显得不那么真实了。
而影响这个问题的 keypoint 就是采样起始时刻 的选择。极端地考虑, 对应采样过程结束, 于是生成的结果就是参考图本身(完全处于参考图流形中); 相反, 代表经历整个 reverse SDE 过程, 由于这是一个随机过程, 因此最终生成的结果就”不那么受控”、随机性比较大, 可能会严重偏离参考图像(被过份地移动至真实图像的流形, 于是远离参考图像所在的流形)。
于是, 越靠近1,生成图像的真实度就会越高,同时由于采样方差更大,因此多样性也越高;而 越靠近0,生成结果与参考图的相似度就越高,同时因为采样方差较小,所以多样性就会变低。
在作者的实验中, 是比较合适的选择, 而实际在面对不同任务时, 建议通过实验去手动调整看效果如何来确定 的选择。
- 局限性
SDEdit 的局限性首先在于其适用场景有限,若参考图像与扩散模型学到的数据域相差较远,可能难以生成既与参考图像相似又看起来真实的图片(考虑参考图像流形与真实图像流形相距甚远而得不到交集的情况)。
其次,为了兼顾生成图像的真实度与参考图像的相似度,需要手动调整采样起始时刻。
还有,为了获得满意的生成效果,可能要重复多次“加噪-去噪”的采样过程。
- 核心代码
以下是 SDEdit 在面临带 mask 的图像编辑场景时的核心代码实现,CW 在此仅截取关键部分,完整源码请自行参考官方repo(https://github.com/ermongroup/SDEdit/blob/main/runners/image_editing.py%23L119).
# `sample_step` 代表重复 “加噪-去噪” 的采样次数
for it in range(self.args.sample_step):
# 采样起始时刻
total_noise_levels = self.args.t
a = (1 - self.betas).cumprod(dim=0)
e = torch.randn_like(x0)
# 将参考图像加噪至采样起始时刻对应的噪声强度
x = x0 * a[total_noise_levels - 1].sqrt() + e * (1.0 - a[total_noise_levels - 1]).sqrt()
... # 省略
with tqdm(total=total_noise_levels, desc="Iteration {}".format(it)) as progress_bar:
# 迭代去噪采样
for i in reversed(range(total_noise_levels)):
t = (torch.ones(n) * i).to(self.device)
# 扩散模型的去噪采样: p(x_{t-1} | x_t),这里使用的是 VP-SDE
x_ = image_editing_denoising_step_flexible_mask(
x, t=t, model=model,
logvar=self.logvar,
betas=self.betas
)
# 将参考图加噪至当前时刻对应的噪声强度
x = x0 * a[i].sqrt() + e * (1.0 - a[i]).sqrt()
# 把扩散模型的采样结果放到参考图像的对应位置
x[:, (mask != 1.)] = x_[:, (mask != 1.)]
... # 省略
# 将整个采样过程获得的结果放到参考图像对应位置
x0[:, (mask != 1.)] = x[:, (mask != 1.)]扩散模型 VP-SDE 的去噪采样:
def image_editing_denoising_step_flexible_mask(x, t, *,
model,
logvar,
betas):
"""
Sample from p(x_{t-1} | x_t)
"""
alphas = 1.0 - betas
alphas_cumprod = alphas.cumprod(dim=0)
# 此处模型的输出是估计的噪声
model_output = model(x, t)
# 估计的噪声乘以该项等于 \beta(t) 乘以 score
weighted_score = betas / torch.sqrt(1 - alphas_cumprod)
# 参考 Algorithm 5
mean = extract(1 / torch.sqrt(alphas), t, x.shape) * (x - extract(weighted_score, t, x.shape) * model_output)
logvar = extract(logvar, t, x.shape)
noise = torch.randn_like(x)
mask = 1 - (t == 0).float()
mask = mask.reshape((x.shape[0],) + (1,) * (len(x.shape) - 1))
# 若是采样的最后一步,则无需加上随机噪声,这是根据 Tweedie's formula 计算采样均值去噪的结果
# 为避免最终生成的图像模糊
sample = mean + mask * torch.exp(0.5 * logvar) * noise
sample = sample.float()
return sampleILVR
ILVR: Conditioning Method for Denoising Diffusion Probabilistic Models 的核心思想与 SDEdit 在一定程度上有相同之处——引入参考图像的低频信息(图像的大体结构和语义)。
ILVR 使用了线性低通滤波器,在采样过程中将每步采样图像的低通部分替换为参考图像的低通部分,对参考图像进行低通滤波前会先对其按当前时间步的噪声强度进行加噪(
) 。另外,也可以不必在采样的全程都使用替换操作,即可以设置采样到某个时间步之后就不再使用参考图像,而是进行无条件采样生成,这样做会促进生成结果的多样性,但同时也会降低与参考图像的相似性(后续统称条件一致性),这是一种 trade-off.
由上展示的算法流程可知,所谓的 “latent variable” 就是指图像经过低通滤波后剩下的低频信息,ILVR 的做法可看作是“带约束的采样过程”—— 要求每步采样结果的低频信息都要与参考图像的低频信息进行对齐。
ILVR 有一个需要重点考虑的因素就是低通滤波器的下采样因子(对应上面的 scale N)。下采样因子的值越小(下采样倍率越小),所保留的高频细节就越多,从而生成的图像就会与参考图像更加相似,但多样性和真实度就会相对降低。
另外,作者的实验结果表明,ILVR 对于低通滤波器的选择还是比较鲁棒(robust)的。
- 局限性与麻烦点
ILVR 的最大限制之一是要求低通滤波器必须是线性的,因而无法使用神经网络来提取参考图像中更为丰富的语义。其次就是为了在多样性和条件一致性之间做 trade-off,需要手工调整下采样因子和采样过程中参考图像注入的时间范围(conditioning range)。
- 核心代码
以下代码展示了 ILVR 的关键操作,截取自官方 repo(https://github.com/jychoi118/ilvr_adm/blob/main/guided_diffusion/gaussian_diffusion.py%23L550).
def p_sample_loop_progressive(...):
... # 省略
# 下采样和上采样操作
if resizers is not None:
down, up = resizers
# T -> 0 迭代采样
for i in indices:
t = th.tensor([i] * shape[0], device=device)
with th.no_grad():
# p(x_{t-1} | x_t)
out = self.p_sample(
model,
img,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
cond_fn=cond_fn,
model_kwargs=model_kwargs,
)
#### ILVR ####
if resizers is not None:
# 若当前时间步超过 `range_t` 则不使用参考图像
# 即回归到正常的无条件生成
if i > range_t:
# 由于要适配采样结果的 shape,因此下采样后要再上采样回来
out["sample"] = out["sample"] - up(down(out["sample"])) + \
up(
down(
self.q_sample(
model_kwargs["ref_img"], t,
th.randn(*shape, device=device)
)
)
)
yield out
... # 省略以上用到的 resizers 包含了下采样(即 ILVR 的低通滤波器)和上采样操作,具体实现可参考这里(https://github.com/jychoi118/ilvr_adm/blob/main/resizer.py%23L8),源头是来自这个库(https://github.com/assafshocher/ResizeRight),其专门针对图像 resize 操作的诸多问题(issue)进行解决,并无缝支持 Numpy & Pytorch(因而完全可微分).
RePaint
RePaint: Inpainting using Denoising Diffusion Probabilistic Models 主要是针对图像修复(image inpainting)任务而提出的,它的做法其实与 SDEdit 的 editing with mask(如前面的 Algorithm 3)相似,输入除了参考图像以外还有一个 mask 用于指示待修复的部分,这部分将用模型采样生成的结果来填充,其余部分则维持与参考图像一致。
(ps: 以上对于 的计算有误, 右边应该对应 , 但结合后文所展示的代码实现后, 或许能够知道为何上面会是 )
由于 mask 内由模型生成的部分与 mask 外参考图像的部分是没有相互进行考虑的,相当于将模型的采样结果“硬塞”到参考图像中被 mask 掉的区域,因此这样难免会造成整幅图像语义上存在不和谐的现象。虽然每次在生成下一步采样结果时,模型都试图对这两部分进行协调,但随着采样过程的进行,采样方差逐渐减小,于是模型对这种不和谐现象进行改造的力度则愈发变小,最终很可能就无法生成一幅语义和谐的图像。
对此, 作者引入 “resampling” 技术, 即对每步采样后的结果重新加噪 (e.g. ), 回到噪声强度更高的阶段, 然后再实施去噪采样, 也可以指定对采样结果加噪多步(e.g. )。因为加噪后采样方差变大了, 所以留给模型纠正这种不和谐现象的空间也就更广了。
以上展示的算法流程是每步采样后仅加噪1步的示例,这个加噪步数在论文中被称为 “jump length”; 代表每个时间步要实施 resampling 多少次, 对应论文中的超参 。
在实际进行采样时,可以预先计算出时间步的变化情况,作者称其为 “time schedule”。这样,每步迭代时,先与下一个时间步进行比较,若比当前时间步大,则代表要实施加噪;否则,就代表要进行去噪采样。
RePaint 的主要局限显而易见 —— resampling 可能导致生成满意的结果需要较长时间,并且也无法保证模型一定就能纠正语义不和谐的问题。另外,适用场景也十分有限,仅仅是 image inpainting with mask 这种。
- 核心代码
以下展示了 RePaint 的核心代码,截取自官方 repo(https://github.com/andreas128/RePaint/blob/main/guided_diffusion/gaussian_diffusion.py%23L510),涉及 time schedule 的计算、结合 mask 的去噪采样 以及 resampling.
# 预先计算 time schedule
times = get_schedule_jump(**conf.schedule_jump_params)
# 把相邻时间步配对
time_pairs = list(zip(times[:-1], times[1:]))
... # 省略
for t_last, t_cur in time_pairs:
... # 省略
t_last_t = th.tensor([t_last] * shape[0], # pylint: disable=not-callable
device=device)
# 去噪采样
if t_cur < t_last: # reverse
with th.no_grad():
image_before_step = image_after_step.clone()
# p(x_{t-1} | x_t)
out = self.p_sample(
model,
image_after_step,
t_last_t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
cond_fn=cond_fn,
model_kwargs=model_kwargs,
cnotallow=conf,
pred_xstart=pred_xstart
)
image_after_step = out["sample"]
pred_xstart = out["pred_xstart"]
sample_idxs[t_cur] += 1
yield out
# 加噪 resampling
else:
# 代表加噪几步,默认是1步
t_shift = conf.get('inpa_inj_time_shift', 1)
image_before_step = image_after_step.clone()
# 回到更噪的水平 p(x_{t+t_shift} | x_t)
image_after_step = self.undo(
image_before_step, image_after_step,
est_x_0=out['pred_xstart'], t=t_last_t+t_shift, debug=False
)
pred_xstart = out["pred_xstart"]去噪采样:
def p_sample(...):
... # 省略
# 第一步采样之后 `pred_xstart` 才不是 `None`
# 这说明在采样了一步之后(从而当前不是纯噪声)才会将参考图像与采样结果相结合
if pred_xstart is not None:
''' gt 指参考图像,将参考图像加噪至当前时间步的噪声水平 '''
gt_weight = th.sqrt(alpha_cumprod)
gt_part = gt_weight * gt
noise_weight = th.sqrt((1 - alpha_cumprod))
noise_part = noise_weight * th.randn_like(x)
# 加噪后的参考图像
weighed_gt = gt_part + noise_part
# 根据 mask 将参考图像与采样结果相结合
x = gt_keep_mask * weighed_gt + (1 - gt_keep_mask) * x
# p(x_{t-1} | x_t)
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
... # 省略由上可知,RePaint 在实现时,是先将参考图像与上一步采样结果相融合,然后再给扩散模型去采样下一步结果的,并非像上面 Algorithm 1 所示是先采样出结果再融合参考图像。并且,第一步采样是不考虑参考图像的,只有待当前采样图像变为非纯噪声之后才会考虑融合参考图像。
resampling 加噪就是正常的扩散模型的加噪过程:
def undo(self, image_before_step, img_after_model, est_x_0, t, debug=False):
return self._undo(img_after_model, t)
def _undo(self, img_out, t):
beta = _extract_into_tensor(self.betas, t, img_out.shape)
img_in_est = th.sqrt(1 - beta) * img_out + th.sqrt(beta) * th.randn_like(img_out)
return img_in_est总结
SDEdit 应该是最早成功应用预训练无条件扩散模型来实现图生图的 training-free 方法之一,可谓是这个领域的开创性先锋,其后出现的 ILVR 和 RePaint 估计或多或少都有从它那里受到启发。比如 ILVR 的 conditioning range 其实就与 SDEdit 从中间时刻开始采样是相同的原理,限制了条件(即参考图)的影响时间范围;而 RePaint 的 resampling 其实几乎就是 SDEdit 反复 “加噪-去噪”的那一套。
最后就为这三兄弟来个总结叭~
线性逆问题
接下来介绍的这批方法主要是针对图像处理的线性逆问题(linear inverse problem) 而提出的,在数学形式上通常可以将逆问题表示为:
其中 是观测量(measurements), 代表观测噪声, 是线性退化(degradation)算子, 通常以矩阵形式来表示, 则是期望恢复的原图。
构造不同形式的 则可以对应到不同类型的图像修复(restoration)任务, 比如:去噪 (denoising)、编辑和填充(inpainting)、超分(super resolution)、上色(colorization)、去模糊 (deblurring) 等。其实, 上一章所介绍的一些场景都可以被归纳至线性逆问题中。
在这种逆问题的设定下, 生成模型的目标就是要建模后验分布 。为便于求解, 通常会将观测噪声假设为高斯噪声。再进一步结合已知的观测量和退化算子, 使得后验分布的建模变得 tractable.
DDRM
DDRM(Denoising Diffusion Restoration Models) 从变分推断(variational inference) 的角度出发,构造了一种后验采样的方法,从而可以利用预训练的(即无需二次训练)无条件扩散模型来解决任意线性逆问题。
DDRM 将求解逆问题的后验分布定义为以观测量为条件的马尔科夫链,这是模型建模的过程;同时将采样过程构造为以观测量为条件的变分分布,这是模型建模所要对齐的目标。
与正常的扩散模型一样,对齐以上两个过程实质上等价于最大化 ELBO(Evidence Lower BOund),并且作者在论文附录 C 中证明了,在一定条件下这个 ELBO 与无条件训练的 DDPM/DDIM 的 ELBO 是等价的,这是预训练无条件扩散模型能够直接用于 DDRM 求解逆问题的关键之一。
另外, 作者构造的变分分布满足边缘分布 , 即扩散模型 VE-SDE 的形式; 同时在附录 B 中, 作者证明了通过适当转换, 也可使用 VP-SDE 的形式, 只需要在每步采样时将 除以 即可转换到 VP-SDE 的状态。
DDRM 最骚的操作在于对退化算子 进行奇异值分解(SVD), 从而在谱空间(spectral space) 中看待扩散过程。之所以这么做, 是因为奇异值分解能够根据奇异值大小来决定观测量 对于原图 的影响程度, 进一步将观测噪声与扩散过程中 的噪声进行”绑定”(通过构造变分分布的方差来维持原扩散过程的噪声强度), 从而确保无条件扩散模型能够正确去噪。
并且,通过 SVD,我们可以知道观测量中缺失的但原始信号 应该拥有的部分,它们对应为奇异值等于0的那些部分,然后利用扩散模型来生成它们。同时,由于扩散模型的采样过程是去噪过程,因此观测噪声也会被去噪,有利于恢复原图质量。
作者构造的变分分布的具体形式如下:
是 的伪逆,在后者奇异值为 的位置,前者则对应为 。对于以上(4),(5),咋一看容易懵逼,但是冷静下来分析就会发现这波构造还是有理可依的。
从顶层设计来说,分为奇异值大于 0 和等于 0 的情况。等于 0 代表观测量没有对原始信号提供有用信息,因此直接使用扩散模型的无条件采样即可;大于 0 时则取决于谱空间中的观测噪声强度( )与原扩散过程的噪声强度 的情况。但无论两者大小如何, 都保证方差与原来扩散模型的一样是 ,从而满足边缘分布 。
为何说以上构造出来的变分分布维持了方差是 ? 这看上去不像啊..
先让我们把目光聚焦至谱空间:
然后再把上面 (4),(5) 中含有 的地方用上式代进去,就会发现分布的方差是 ,均值是 。至于 (5) 中的第一个分布, 由于使用的扩散过程是 VE-SDE, 因此 , 于是 就是标准高斯噪声, 从而整个分布的方差就是 , 均值则是 。
所以说, 作者所构造出来的变分分布妥妥地满足了边缘分布 , 和扩散过程是一致的, 这也是无条件扩散模型能够直接用于 DDRM 求解逆问题的关键!
OK,变分分布和无条件扩散模型“对齐”了,现在就可以考虑生成模型所建模的分布了。
虽然上面写着 “trainable parameters
“,但前面说过,作者证明了将 (7), (8) 和 (4), (5) 进行对齐所对应的 ELBO 等价于无条件扩散模型在训练时所对应的 ELBO。于是,非常幸运地,相当于预训练无条件扩散模型就足以 cover 住 (7), (8) 了!
在论文附录 C 中,作者证明了当 的情况下,DDRM 的 ELBO 能够完美对齐无条件扩散模型的 ELBO,即:
当 选择其它值时, DDRM 的 ELBO 也正比于 , 所以预训练的无条件扩散模型也是一个不错的最优解平替。
顺便吹一下, 作者还在论文附录 H 中证明了 ILVR 可以被看作是 DDRM 在没有观测噪声情况下的特例, 其中退化算子 是下采样矩阵。
- 局限性
DDRM 虽然思路新奇,足够秀,但确实不太“新手友好”,首先难免会吐槽这点。
然后,SVD 虽然对于矩阵分析是很有帮助的,但在高维空间下计算量会比较大。
其次,作者 hand-craft 的变分分布和采样分布难免让人“感觉不稳”,面临实际场景时的效果还有待考量。
最后,DDRM 的只能解决线性的逆问题,并且需要预先知道退化算子的数学形式(当然也可以通过构造来近似)。
- 核心代码
DDRM 涉及的数学公式不少,代码实现当然也比较复杂,有点那种一眼看去还没入门就想放弃的赶脚..
但其实只要耐下心来,对照着论文公式去读代码,就会发现还是“有理可依、有迹可循”的(不对照着论文公式去读的话容易晕,还请三思而后行)。 CW 将 DDRM 的核心代码从官方库(https://github.com/bahjat-kawar/ddrm/blob/master/functions/denoising.py%23L11)截取下来并附上了关键注释,各位友友们要是实在太闲不妨可以看看。
由于 DDRM 在理论上使用的是 VE-SDE,但在代码实现中,扩散模型的采样用的却是 VP-SDE 的形式,因此需要来回在 VE-SDE 和 VP-SDE 之间的状态( )进行切换,这点需要注意一下。
def efficient_generalized_steps(x, seq, model, b, H_funcs, y_0, sigma_0, etaB, etaA, etaC, cls_fn=None, classes=None):
with torch.no_grad():
''' setup vectors used in the algorithm '''
# 退化矩阵 H 的奇异值
singulars = H_funcs.singulars()
# 奇异矩阵
Sigma = torch.zeros(x.shape[1]*x.shape[2]*x.shape[3], device=x.device)
Sigma[:singulars.shape[0]] = singulars
# $U^Ty$
U_t_y = H_funcs.Ut(y_0)
# $\bar{y}$ 观测量在谱空间中的表示
Sig_inv_U_t_y = U_t_y / singulars[:U_t_y.shape[-1]]
''' initialize x_T as given in the paper '''
# VP-SDE 的 \alpha_T
largest_alphas = compute_alpha(b, (torch.ones(x.size(0)) * seq[-1]).to(x.device).long())
# VE-SDE 的 sigma_T,根据论文附录 B 中 \alpha_t 和 \sigma_t 的转换关系计算
largest_sigmas = (1 - largest_alphas).sqrt() / largest_alphas.sqrt()
# 判断奇异值是否足够大
large_singulars_index = torch.where(singulars * largest_sigmas[0, 0, 0, 0] > sigma_0)
inv_singulars_and_zero = torch.zeros(x.shape[1] * x.shape[2] * x.shape[3]).to(singulars.device)
# 奇异值比较大的位置则设为 $\frac{\sigma_y}{s_i}$,否则为0
inv_singulars_and_zero[large_singulars_index] = sigma_0 / singulars[large_singulars_index]
inv_singulars_and_zero = inv_singulars_and_zero.view(1, -1)
''' implement p(x_T | x_0, y) as given in the paper '''
# if eigenvalue is too small, we just treat it as zero (only for init)
init_y = torch.zeros(x.shape[0], x.shape[1] * x.shape[2] * x.shape[3]).to(x.device)
init_y[:, large_singulars_index[0]] = U_t_y[:, large_singulars_index[0]] / singulars[large_singulars_index].view(1, -1)
init_y = init_y.view(*x.size())
# 根据论文(7)的分布计算
remaining_s = largest_sigmas.view(-1, 1) ** 2 - inv_singulars_and_zero ** 2
remaining_s = remaining_s.view(x.shape[0], x.shape[1], x.shape[2], x.shape[3]).clamp_min(0.0).sqrt()
# \bar{x}_T
init_y = init_y + remaining_s * x
# 从 VE-SDE 转换为 VP-SDE 的状态,根据论文附录 B 计算
# 由于 $\sigma_T$ 较大,因此这里将 $\sqrt{1 + \sigma_T^2}$ 近似为 $\sigma_T$
init_y = init_y / largest_sigmas
''' setup iteration variables '''
# 由谱空间转换回来:$V^Tx$ -> $x$
x = H_funcs.V(init_y.view(x.size(0), -1)).view(*x.size())
n = x.size(0)
seq_next = [-1] + list(seq[:-1])
x0_preds = []
xs = [x]
''' iterate over the timesteps '''
for i, j in tqdm(zip(reversed(seq), reversed(seq_next))):
t = (torch.ones(n) * i).to(x.device)
next_t = (torch.ones(n) * j).to(x.device)
at = compute_alpha(b, t.long())
at_next = compute_alpha(b, next_t.long())
xt = xs[-1].to('cuda')
''' 扩散模型估计噪声 '''
if cls_fn == None:
et = model(xt, t)
else:
et = model(xt, t, classes)
et = et[:, :3]
et = et - (1 - at).sqrt()[0,0,0,0] * cls_fn(x,t,classes)
if et.size(1) == 6:
et = et[:, :3]
# prediction of x0
# 根据当前状态 $x_t$ 和 估计的噪声 `et` 预测原图 `x0_t`
x0_t = (xt - et * (1 - at).sqrt()) / at.sqrt()
''' variational inference conditioned on y '''
sigma = (1 - at).sqrt()[0, 0, 0, 0] / at.sqrt()[0, 0, 0, 0]
sigma_next = (1 - at_next).sqrt()[0, 0, 0, 0] / at_next.sqrt()[0, 0, 0, 0]
# 由 VP-SDE 的状态转换至 VE-SDE 的状态以便执行 DDRM 在谱空间的采样过程
# 根据论文附录 B 计算:$x_t = x_t \sqrt{1+sigma_t} = \frac{x}{\alpha_t}$
xt_mod = xt / at.sqrt()[0, 0, 0, 0]
# $\bar{x}_t$
V_t_x = H_funcs.Vt(xt_mod)
SVt_x = (V_t_x * Sigma)[:, :U_t_y.shape[1]]
# $\bar{x}_{\theta, t}$
V_t_x0 = H_funcs.Vt(x0_t)
SVt_x0 = (V_t_x0 * Sigma)[:, :U_t_y.shape[1]]
falses = torch.zeros(V_t_x0.shape[1] - singulars.shape[0], dtype=torch.bool, device=xt.device)
cond_before_lite = singulars * sigma_next > sigma_0
cond_after_lite = singulars * sigma_next < sigma_0
cond_before = torch.hstack((cond_before_lite, falses))
cond_after = torch.hstack((cond_after_lite, falses))
''' 用于 p^{(t)}_{\theta}(\bar{x}^{(i)}_{t-1} | x_t, y) '''
# 用于 $s_i = 0$ 的情况
# $\eta \sigma_{t-1}$
std_nextC = sigma_next * etaC
# \sqrt{1-\eta^2} \sigma_{t-1}$
sigma_tilde_nextC = torch.sqrt(sigma_next ** 2 - std_nextC ** 2)
# 用于 $\sigma_t < \frac{\sigma_y}{s_i}$ 的情况
std_nextA = sigma_next * etaA
sigma_tilde_nextA = torch.sqrt(sigma_next**2 - std_nextA**2)
# 用于 $\sigma_t >= \frac{\sigma_y}{s_i}$ 的情况
diff_sigma_t_nextB = torch.sqrt(sigma_next ** 2 - sigma_0 ** 2 / singulars[cond_before_lite] ** 2 * (etaB ** 2))
# missing pixels, $s_i = 0$
Vt_xt_mod_next = V_t_x0 + sigma_tilde_nextC * H_funcs.Vt(et) + std_nextC * torch.randn_like(V_t_x0)
# less noisy than y (after) $\sigma_t < \frac{\sigma_y}{s_i}$
Vt_xt_mod_next[:, cond_after] = \
V_t_x0[:, cond_after] + sigma_tilde_nextA * ((U_t_y - SVt_x0) / sigma_0)[:, cond_after_lite] + std_nextA * torch.randn_like(V_t_x0[:, cond_after])
#noisier than y (before) $\sigma_t >= \frac{\sigma_y}{s_i}$
Vt_xt_mod_next[:, cond_before] = \
(Sig_inv_U_t_y[:, cond_before_lite] * etaB + (1 - etaB) * V_t_x0[:, cond_before] + diff_sigma_t_nextB * torch.randn_like(U_t_y)[:, cond_before_lite])
# aggregate all 3 cases and give next prediction
# 由谱空间转换回来 \bar{x}_{t-1}=V^Tx_{t-1} -> x_{t-1}
xt_mod_next = H_funcs.V(Vt_xt_mod_next)
# 从 VE-SDE 状态转换至 VP-SDE 状态
# 根据附录 B 计算:x_t = $\frac{x_t}{\sqrt{1+\sigma_{t-1}^2}} = x_t \sqrt{\alpha_t}$
xt_next = (at_next.sqrt()[0, 0, 0, 0] * xt_mod_next).view(*x.shape)
x0_preds.append(x0_t.to('cpu'))
xs.append(xt_next.to('cpu'))至于退化矩阵 H_funcs 的计算,可以根据不同场景来构造,具体见这部分代码,CW 就不再这里赘述了。
DDNM
如果说前面的 DDRM 让你感到思路新奇,那么即将出场的 DDNM(Zero-Shot Image Restoration Using Denoising Diffusion Null-Space Model) 比起它来可谓是有过之而无不及~
DDNM 可以解决任意形式的线性逆问题,它的核心思想是利用了向量空间的 range-null space decomposition(零值域分解),通过在采样过程中持续校正(refine)零空间的部分(null-space contents),就可以使得预训练无条件扩散模型生成真实且满足条件一致性(data-consistent)的结果,可谓是“novel 感”满满~
OK,CW 知道以上这段话会让大部分友友们感觉说了等于没说,DDNM 究竟是怎么 work 的?什么是 range-null space decomposition?校正 null-space contents 具体又是什么鬼?…
稍安勿躁,接下来 CW 为您一一揭晓~
- Range-Null Space Decomposition
假设有矩阵 , 其伪逆(pseudo-inverse) 为 , 满足 . 那么, 对于向量 就可以把其投影到 的值空间(range-space), 因为: ;另一方面, 则可以将其投影至零空间(null-space), 因为:. 有意思的是, 任意向量 都可以分解为两部分,其中一部分位于矩阵 的 range-space, 而另一部分则位于 null-space:
- Refine Null-Space
先简单考虑不含噪声的线性逆问题 , 其中 代表观测量, 是原图(i.e. groundtruth), 是线性退化 (degradation)矩阵。解决该问题的目标就是要找到(生成)一张图 从而满足:
其中 代表原图所服从的分布。以上目标中的前一项代表了(条件)一致性(consistency),后一项则代表真实性(realness)。如果对原图进行 range-null space decomposition,根据前面的式子,可以得到:
于是不妨遵循以上形式来构造我们想要生成的目标:
这样,我们求解的目标就变为 。并且,无论其取值如何,都不影响 consistency,因为:
于是, consistency 的问题我们不用操心, 只需重点关注 , 也就是 null-space contents, 以便尽可能满足
, 即 realness.
说到生成, 那可是扩散模型的拿手好戏! 由于 是已知量, 因此扩散模型只负责生成 这部分就好。但这部分并非是用每步采样的结果(i.e. ), 因为刚刚在构造目标形式解时是依据原图的 range-null space 启发而来的, 所以 这部分要用扩散模型每步采样时所估计的原图 来代替。若使用 DDPM, 则为:
用上式来代替 并代入到前面所构造的目标形式解中:
这起到了校正无条件扩散模型所估计的 的效果,从而约束其满足 consistency.
DDPM 在采样时所依据的分布 是高斯分布,其中均值和方差为:
将以上 用前面校正后的结果 替代, 便可以得到下一步的采样结果:
整个采样流程如下:
- 同时满足 consistency & realness
通过前面部分可知, 我们对于逆问题所构造的目标形式解 是天然满足 consistency 的, 这点不用担心。并且, 最后一步的采样结果就是 , 于是 consistency 依然满足。而 realness 所对应的 null-space contents, 我们交给了扩散模型来 handle, 即 , 但它与 range-space 所对应的 天然是”割裂”的, 论文中称之为 “disharmony” 现象。
不过,由于 DDNM 在每步采样时都将 range-space contents 和 null-space contents 代入到采样分布中得到下一步采样结果 , 它相当于是 的 noised version. 于是,这其中的 noise 无意间便起到了消除 disharmony 的作用——想象下,将原本是“隔开”的、没有交集的 range-sapce 和 null-space 通过添加噪声来扰动,使它们的覆盖范围都变大,于是便产生了交集,类似于在 SDEdit 那一章所展示的原理图。
这么一来,就会使得 range-space in harmony with null-space,于是最终生成的结果就可以同时满足 consistency & realness.
以上针对的线性逆问题均以不含噪声(noise-free)为前提,如今我们一起来把目光转向到带有观测噪声的情况。
对于含有观测噪声的情况, 由于在 中夹带的噪声 (源于 ) 会被引入到下一步的采样结果 中, 因此作者选择对 这部分进行 scale(于是引入 ), 这部分可看作是 range-space contents 对于 的校正, 是保证 consistency 的关键。然后进一步构造采样方差( )与原本无条件扩散模型的采样方差进行绑定, 这与前面 DDRM 的做法类似, 为的是不改变无条件扩散模型在采样时的噪声强度, 这样模型基于原来每个时间步的 SNR(信噪比) 所估计的噪声就能够适用, 从而可以成功去噪。
那么,对 range-space contents 的 correction 进行 scale 的道理在哪呢?
可以这么想:由于夹带了噪声,就相当于 range-space contents 的校正作用受到了影响(被噪声扰动),从数学表达式来看,以上 (16) 式中的蓝色部分是可以被合并到其前一项的(从而得到 ),这就直接体现了 correction 的程度受到了影响,因此不妨直接引入一个 scale 系数来表达这种影响,同时还能够控制影响程度。
在之前 noise-free 的情况下,原本的下一步采样结果为:
结合 (17),(18) 式, 如今 那部分就会多出一个强度为 的噪声项(想象下 (17) 式括号内还有一项 , 并且 变为 。暂且考虑最简单的情况, 即 , 并假设 具有单位尺度, 同时记上式 的系数为 , 要使得 的方差不改变 (等于 ), 则需满足:
之所以在 的情况下令 是希望在观测噪声不大(对于 range-space contents 的影响较小)的情况下尽量削弱其影响,以尽量与前面 noise-free 的情况接近,从而最大化 range-space contents 的校正作用,以便保证 consistency.
对于一般化的情况,作者在论文附录 I 中给出了详细的解析,原理类似,还请各位靓仔靓女们自行去细细品味,CW 要偷懒一下~
另外,作者不小心发现 DDNM 在面临一些场景时生成结果的真实性(realness)不太能看,比如:大尺度均值池化下的 SR(超分) 任务、低采样率的 CS(压缩感知) 任务以及大部分内容被 mask 掉的 inpainting 任务等。作者对此归因为 range-space contents 过于局部(从而模型看到的内容太少)以至于无法引导模型生成一个全局 harmony(同时满足 consistency & realness) 的结果。
In these cases, the range-space contents A†y is too local to guide the reverse diffusion process toward yielding a global harmony result.
既然生成的结果不够真实,那就“回流再造”,直至 KPI 达标(生成满意的结果)为止,模型还不是如打工人一样是牛马!在这种念头的驱动下,作者发现前辈 RePaint 就这么玩过(RePaint 中提出的 resampling 方法),于是“借鉴”过来小改一下随即对外宣称为 “time-travel” 技术。
具体地,在采样的每个时间步,可以选择重新加噪回前面更 noised 的阶段,然后再继续实施去噪采样。至于具体加噪几步,则可以用一个超参 来控制。直观来看,这是一种“以更好的过去来产生更好的未来”的思路。
Intuitively, the time-travel trick produces a better “past”, which in turn produces a better “future”.
DDNM 在时间步 的采样依赖于 , 在直觉上, 它应该比之前在 时间步所估计的 来得好。于是, 从 加噪回去, 相当于利用了更好的 所携带的信息, 这一步相当于是 , 然后重新由 时间步进行去噪采样直至 时, 就会产生更好的结果, 因为中间每步迭代生成都继承了”更好的产生更好的”, 最终生成的结果也就更好。
结合 time-travel 技术,在解决含噪声的逆问题时,DDNM 进化为 ,整个采样流程如下:
- 局限性
DDNM 主要局限在于需要明确知道退化矩阵的数学形式并计算其伪逆(或者人为构造),并且只能解决线性的逆问题。其次,time-travel 会导致生成满意的效果需要较长时间。另外,对于有观测噪声的情况,需要将噪声强度绑定到扩散模型的采样方差,引入了手工设计的参数。
CW 顺便提一嘴,在 DDNM 论文的附录 H 中,作者证明了 RePaint 和 ILVR 都是 DDNM 在 noise-free(不含观测噪声)下的特例;同样,在这种情况(i.e. noise-free)下,DDRM 也可视作是 DDNM 的特例。
- 核心代码
以下代码截取自官方 repo(https://github.com/wyhuai/DDNM/blob/main/guided_diffusion/diffusion.py%23L368),对应以上 Algorithm 2.
至于线性退化矩阵的实现,作者给出了一些简单场景的参考:
def color2gray(x):
coef=1/3
x = x[:,0,:,:] * coef + x[:,1,:,:]*coef + x[:,2,:,:]*coef
return x.repeat(1,3,1,1)
def gray2color(x):
x = x[:,0,:,:]
coef=1/3
base = coef**2 + coef**2 + coef**2
return th.stack((x*coef/base, x*coef/base, x*coef/base), 1)
def PatchUpsample(x, scale):
n, c, h, w = x.shape
x = torch.zeros(n,c,h,scale,w,scale) + x.view(n,c,h,1,w,1)
return x.view(n,c,scale*h,scale*w)
# Implementation of A and its pseudo-inverse Ap
if IR_mode=="colorization":
A = color2gray
Ap = gray2color
elif IR_mode=="inpainting":
A = lambda z: z * mask
Ap = A
elif args.deg =='denoising':
A = lambda z: z
Ap = A
elif IR_mode=="super resolution":
A = torch.nn.AdaptiveAvgPool2d((256 // scale, 256 // scale))
Ap = lambda z: PatchUpsample(z, scale)
elif IR_mode=="old photo restoration":
A1 = lambda z: z * mask
A1p = A1
A2 = color2gray
A2p = gray2color
A3 = torch.nn.AdaptiveAvgPool2d((256 // scale, 256 // scale))
A3p = lambda z: PatchUpsample(z, scale)
A = lambda z: A3(A2(A1(z)))
Ap = lambda z: A1p(A2p(A3p(z)))
y = A(x_orig)此外,作者还给出了一个应用 SVD 来实现线性退化矩阵 AA 的版本,具体可参考https://github.com/wyhuai/DDNM/blob/main/functions/svd_operators.py%23L211,该版本的采样过程对应于论文附录 I 的内容,其代码实现可参考https://github.com/wyhuai/DDNM/blob/main/guided_diffusion/diffusion.py%23L419。
总结
不难发现,DDRM 和 DDNM 在思想上是有些相似的——都是利用了向量/矩阵空间的分解技术,在那个空间去看待扩散过程,以便将观测信息注入至无条件扩散模型(的采样过程)中。为了能够成功利用扩散模型进行去噪,二者都通过 hand-craft 的方式来与原来无条件的情况(无条件扩散模型预训练时)对齐每个时间步的噪声强度。另外,两篇论文的作者们都偏好将以往的方法视作它们的特例,就有一种喜欢强调自己方法更 general 的调性(不带褒贬地说出事实)~
Guidance 的影子
在本文介绍的所有方法中,除了 SDEdit 以外,其余或多或少都瞥见了 guidance 的影子。ILVR 和 RePaint 是对每步的采样结果 进行校正,而 DDRM 和 DDNM 则是对每步所估计的原图 进行校正。校正是为满足一致性(consistency),这本质上同属 guidance 的效果。
具体地,对于 ILVR:
对于 RePaint:
对于 DDRM 来说, guidance term 则更为明显一把采样分布均值中的 单独提取出来, 其余部分便可视作 guidance term, 只不过这是在 spectral space 中对 做引导(即对 进行校正)。
最后,对于 DDNM,前面的式 (17) 更是将“guidance 风范”展露无遗,连 guidance scale 都用上了:
嗯,相信各位友友们都猜到了 —— CW 将会在下一篇文章里大(吹)聊(水) guidance 方法,从而继续为这份食谱增添一些诱人的配方~
#SPLAM
基于子路径线性近似的扩散模型加速方法
本工作主要解决扩散模型在采样过程中需要多步导致推理速度较慢,针对现有的LCM存在的累积误差较大的问题进行优化,通过提出线性ODE采样方法,进一步提升了生图的质量和速度。在四步推理的设置下,在COCO30k和COCO5k上分别取得了10.06和20.77的FID分数,在加速模型方法中达到了SOTA效果。
本文介绍南京大学和阿里巴巴在扩散模型加速任务上的新工作:SPLAM: Accelerating Image Generation with Sub-Path Linear Approximation Model。本工作主要解决扩散模型在采样过程中需要多步导致推理速度较慢,针对现有的LCM存在的累积误差较大的问题进行优化,通过提出线性ODE采样方法,进一步提升了生图的质量和速度。在四步推理的设置下,在COCO30k和COCO5k上分别取得了10.06和20.77的FID分数,在加速模型方法中达到了SOTA效果。
目前我们的工作已被 ECCV 2024 接收为 Oral,论文、代码、模型均已开源:
项目主页:https://subpath-linear-approx-model.github.io/
论文:https://arxiv.org/abs/2404.13903
代码:https://github.com/MCG-NJU/SPLAM
引言
扩散模型目前已经成为文本生成图片领域使用最为广泛的模型,其通过逐步去噪步骤来从一张高斯噪声采样生成真实分布中的图片。然而,扩散模型一直存在的一个问题是其运行速度,因为需要多步迭代推理,导致图片生成速度缓慢,计算开销大。针对这个问题一直以来,也有非常多的工作在探索加速扩散模型的方法。在最初的DDPM中,模型的推理需要和训练时相同的1000步迭代,生成一张图片通常需要数分钟。一系列工作着重研究推理时的采样方法,如DDIM,DPM-Solver等,这些方法通过ODE等技术优化,将采样步数从1000步降低到了20~50步量级,大大提升了图片生成速度。另外一系列的工作着重研究基于现有预训练模型(比如Stable Diffusion),通过蒸馏等方法将步数进一步压缩,实现到了10步以下的采样迭代次数。如一致性模型,通过将PF-ODE上的采样点映射到原点的思想,实现了2-4步的推理,然而压缩步数也会导致一定程度的图片质量下降。我们的论文主要分析了一致性优化学习的过程中的难点和导致性能下降的因素,提出了子路径线性近似模型(SPLAM)尝试缓解这些问题,实现了更小的累积误差,提升了模型性能。
方法简介
一致性模型
一致性模型(Consistency Model)[1] 是 OpenAI 的 Song Yang 博士在 ICML2023 提出的扩散模型加速方法,是这个领域中非常重要的一项工作,基于此在Stable Diffusion上开发的LCM模型 [2] 也是在用户社区中热度非常高加速功能插件,我们首先来回顾一下一致性模型的原理。
根据 Song Yang [3] 的理论,一个扩散模型的去噪过程可以建模为一条常微分方程ODE路径,称为概率流Probability-Flow ODE (PF-ODE):
而一致性模型的想法其实也非常简单,就是将ODE路径上每一个点都映射到原点,而原点来源于真实图片的分布,从而做到一步生成,如图所示:
具体地, 我们希望学习一个函数 , 对于一条ODE上的采样点 。在训练中, 从 逐步采样到 通常时间开销过大, 所以CM采取了一个训练技巧, 在每一步训练迭代中通过缩小相邻两个点间的映射误差, 来逐渐最终达到一致性。然而这也带来了问题, 逐步的收玫导致了较大的累积误差:
使得在生图时的图片的细节丢失较多,生图质量较差。我们的方法也是针对这个问题,通过在每个子路径上通过随机线性插值采样,来进行连续的渐进式的误差估计,做到累计误差更小的去噪映射。
问题分析
对于上面提到的一步生成模型,我们通常把映射函数参数化为:
根据EDM中的理论, 我们可以设计一个 canonical denoiser function: ,而其去噪目标就为 : 。这时会存在一个问题, 这个目标其实比较难以优化,原因在于随着时间步 的增加, 会逐渐趋向于零,这会使得训练不稳定有可能塌缩。一致性模型其实一定程度上缓解了这个问题, 当我们假设模型理想地收敛, 即 , 这个性质能够对于上式进行一个预估: 。然后我们把 的表达式代入,得到一个基于 的误差估计:
因为额外有了系数 ,所以上面所提到的问题被一定程度的缓解。
现在我们再来具体分析一下这个优化目标,我们可以把它解耦为两项:
(1) , 这一项衡量了由于漂移和扩散过程导致的从 到 的增量距离。
(2) , 这一项衡量了前一时间步的去噪贡献, 这些贡献会连续地传播到后续时间步。
这时,我们我们就可以把这个优化目标重写为一个子路径(Sub-Path)的优化目标:
在这个目标式中,这项是导致累积误差的关键,我们也着重对于这项进行优化。
SPLAM
基于此,我们提出了我们的加速方法子路径线性近似模型(Sub-Path Linear Approximation Model,SPLAM),如图所示。
首先, 我们提出了子路径线性 ODE(Sub-Path Linear ODE, SL-ODE), 来近似原始PF-ODE上的子段, 由此来进行对于 的递进式估计。具体来说, 对于原始路径上的一段 , 基于 我们对两个端点 进行插值形成线性路径, 在这个线性路径上的采样点可以表示为:
因为 符合由PF-ODE控制的分布, 我们的线性变换有效地定义了一个对于 的线性 ODE:
即为SL-ODE。注意到这里对于端点多了一项漂移系数 , 这项系数的引入具体可参考我们论文中的详细推导。据此, 我们也有了对应 的Denoiser和生成表达式:
将这个式子代入上面的子路径优化目标,便得到了我们SPLAM的最终优化目标:
这个目标对于原本较难优化的 dist 项提供了一种递进式的拟合,这也使得我们我们的训练可以使用更大的推理步长。
由此,我们也以预训练好的Stable Diffusion模型作为PF-ODE,来建立我们的SL-ODE,并提出了基于SPLAM目标的蒸馏方法(Sub-Path Linear Approximation Distillation,SPLAD)。我们依然沿用CM中的生成函数的参数表达式,除了额外增加了一个维度 :
与CM的优化方法结合,SPLAD最小化的目标为:
其中 为使用的教师模型作为 ODE Solver。
具体训练流程如下算法所示:
在推理时, 我们只需设置 即可实现预测出图: ,同样地,我们也采用和CM同样的多步推理策略来实现更好的生成质量。
实验结果
定量指标
在常用的学术指标基准 COCO FID上,我们的SPLAM超过了LCM和其他的加速方法。具体地,在COCO-30k和COCO-5k两个常用的benchmark上,我们都比较了CFG=3时的最优FID分数。此外,在实际使用中我们通常使用较高的CFG值来提升图片质量,我们也测试了在CFG=8下和其他模型的对比,同样取得了最好的FID分数。
定性可视化
- 由于LCM官方只放出了基于DreamShaper训练的LCM权重,我们也基于DreamShaper训练了一版SPLAM,对比结果如下。
- 同时我们也基于SD2.1对齐了训练配置复现了LCM和我们的SPLAM对比。
可以明显地看出,SPLAM由于优化了更小的累积误差,相比 LCM 明显能够保留更多的细节,画出更加清晰的线条和纹理,效果有显著提升。更多的可视化例子可见我们的论文。
总结
本文提出了一个对于扩散模型的加速方法SPLAM,通过子路径线性近似策略来优化一致性学习过程中的累积误差,提升了图片生成质量。我们方法的数学形式推导比较多,但是核心思想还是比较自然,对于原始一致性训练过程中相邻两点的映射误差较难以优化的问题,我们引入额外的一个维度 ,通过建立线性插值进行连续的渐进式的误差估计。在这样的子路径上进行优化使得 SPLAM 的学习更加平滑,能够做到累计误差更小的去噪映射,从而提升更少步数生图的图片质量。
#SCNet
北大、哈工大、清华联合提出无需GT的自监督图像重建网络学习方法
本文提出了一种新颖的自监督可扩展深度压缩感知(CS)方法,名为SCL和SCNet,能够在不需要真实标签的情况下,通过训练在部分测量集上处理任意采样比率和矩阵,显著提升压缩感知的有效性和灵活性。
一、论文信息
论文作者:Bin Chen(陈斌), Xuanyu Zhang(张轩宇), Shuai Liu(刘帅), Yongbing Zhang†(张永兵), and Jian Zhang†(张健)(†通讯作者)
作者单位:北京大学深圳研究生院、清华大学深圳国际研究生院、哈尔滨工业大学(深圳)
发表刊物:International Journal of Computer Vision (IJCV)
发表时间:2024年8月13日
正式版本:https://link.springer.com/article/10.1007/s11263-024-02209-1
ArXiv版本:https://arxiv.org/abs/2308.13777
开源代码:https://github.com/Guaishou74851/SCNet
二、任务背景
作为一种典型的图像降采样技术, 自然图像压缩感知 (Compressed Sensing, CS) 的数学模型可以表示为 , 其中 是原始图像真值(Ground Truth, GT), 是采样矩阵, 是观测值, 是噪声。定义压缩采样率为 。
图像CS重建问题的目标是仅通过观测值 和采样矩阵 来复原出GT x 。基于有监督学习的方法 多现实应用中, 获得高质量的GT数据需要付出高昂的代价。
本工作研究的问题是自监督图像 重建, 即在仅给定一批压缩观测值 和采样矩阵 的情况下, 训练一个图像重建网络
。现有方法对训练数据的利用不充分, 设计的重建网络表征能力有限, 导致其重建精度和效率仍然不足。
三、主要贡献
- 技术创新点1:一套无需GT的自监督图像重建网络学习方法。
如图1 (a) 所示, 在训练过程中, 我们将每组观测数据 )随机划分为两个部分 和 , 并输入重建网络, 得到两个重建结果 和 。我们使用以下观测值域损失函数约束网络产生符合”交叉观测一致性”的结果:
进一步地, 如图1 (b) 所示, 为了增强网络的灵活性和泛化能力, 使其能够处理任意采样率 和任意采样矩阵 的重建任务, 我们对 和 进行随机几何变换(如旋转、翻转等), 得到数据增广后的 和 , 然后使用以下图像域损失函数约束网络, 使其符合”降采样一重建一致性”:
其中 和 、 和 , 以及 和 分别是随机生成的采样矩阵、噪声和采样率。最终, 结合以上两个损失函数, 我们定义双域自监督损失函数为 。
图1:提出的损失函数。
在训练阶段, 我们使用 以无需GT的自监督方式, 学习一个支持任意采样率和采样矩阵的重建网络; 在测试阶段, 除了可以直接使用训练好的网络重建图像外, 也可以使用 在单个或多个测试样本上微调网络, 以进一步提升重建精度。
- 技术创新点2:一个基于协同表示的图像重建网络。
如图2所示,我们设计的重建网络首先通过一个卷积层从观测值、采样矩阵与采样率()中提取浅层特征,并依次注入可学习的图像编码和位置编码。接着,使用多个连续的深度展开网络模块对特征进行增强,每个模块对应于近端梯度下降算法的一个迭代步骤。最后,重建结果由一个卷积层和一个梯度下降步骤产生。
图2:提出的图像重建网络。
我们设计的重建网络结合了迭代优化算法的显式结构设计启发与神经网络模块的隐式正则化约束,能够自适应地学习待重建图像的深度协同表示,展现出强大的表征能力,在重建精度、效率、参数量、灵活性和可解释性等方面取得了良好的平衡。
四、实验结果
得益于提出的双域自监督损失函数与基于协同表示的重建网络,我们的方法在多个测试集(Set11、CBSD68、Urban100、DIV2K、我们构建的数据集)、多种数据类型(模拟/真实数据、1D/2D/3D数据)以及多个任务(稀疏信号恢复、自然图像压缩感知、单像素显微荧光计算成像)上均表现出优异的重建效果。同时,我们的方法展现出了对训练时未见过的采样矩阵与采样率的出色泛化能力。
图3:我们的方法与现有其他方法的对比结果。
更多方法细节、实验结果与原理分析可参考我们的论文。
五、实验室简介
视觉信息智能学习实验室(VILLA)由张健助理教授于2019年创立并负责,专注于AI计算成像与底层视觉、可控内容生成与安全、三维场景理解等研究领域,已在Nature系列子刊Communications Engineering、SPM、TPAMI、IJCV、TIP、NeurIPS、ICLR、CVPR、ICCV和ECCV等高水平国际期刊和会议上发表了50余篇论文。
在计算成像与底层视觉方面,张健助理教授团队的代表性成果包括优化启发式深度展开重建网络ISTA-Net、COAST、ISTA-Net++,联合学习采样矩阵压缩计算成像方法OPINE-Net、PUERT、CASNet、HerosNet、PCA-CASSI,以及基于信息流增强机制的高通量广义优化启发式深度展开重建网络HiTDUN、SODAS-Net、MAPUN、DGUNet、SCI3D、PRL、OCTUF、D3C2-Net。团队还提出了基于自适应路径选择机制的动态重建网络DPC-DUN和用于单像素显微荧光计算成像的深度压缩共聚焦显微镜DCCM,以及生成式图像复原方法Panini-Net、PDN、DEAR-GAN、DDNM,受邀在信号处理领域旗舰期刊SPM发表专题综述论文。本工作提出的自监督重建网络学习方法SCNet进一步减少了训练重建网络对高质量GT数据的依赖。
更多信息可访问VILLA实验室主页(https://villa.jianzhang.tech/)或张健助理教授个人主页(https://jianzhang.tech/)。
#人类的未来是实现 AGI 自由的未来
揭露 DeepMind 对 AGI 的思考与想象。
DeepMind的创始人Demis Hassabis加入AI行业大辩论来分享新观点了。
随着AI技术的突飞猛进,行内人对AI的看法也越来越多样复杂。前有马斯克四处宣扬“AI可能使人类灭亡”,后有Andrew Ng嗤之以鼻“担心超级智能AI的人就像是在担心火星人口太多”,还有奥特曼坚持“加速AI研发才能解决全球挑战”,李飞飞反复强调“必须确保AI为人服务”。
各种论点争得热火朝天,Demis Hassabis也闪亮登场,发表了自己的观点。
Hassabis冷静地指出,现在有些初创公司和投资者已经被 AI 的短期潜力冲昏了头脑。虽然AI 未来的发展潜力无限,但目前那些听起来像科幻电影的目标,其实大多只是噱头,技术远未成熟。要识别这些 AI 公司宣传是真是假,Hassabis 的秘诀是:了解他们的技术背景和趋势,尽量远离那些盲目跟风的公司。
面对当前的 AI 热潮,Hassabis心情复杂。一方面,他怀念AI尚未受到太多关注时的宁静,没有那么多喧嚣和干扰;另一方面,他也认可如今的关注推动了 AI 在现实世界中的积极应用。
虽然Hassabis支持 AI 开源,但也清醒地意识到这背后的巨大风险,特别是 AI 被用作不良目的的潜在威胁。他提出了一个折中方案:延迟发布开源模型,让它们落后于前沿技术一两年,以减少安全隐患。
Hassabis特别强调了对AGI和AI管控的担忧。他认为开源模型一旦发布便无法收回,需更严格的安全措施和测试环境。他提议开发 AI 助手以监控和测试下一代 AI 系统,同时建议在发布 AI 系统时附带使用说明,帮助用户理解其功能和风险。
虽然也有担忧,但Hassabis对实现AGI的未来抱有极其乐观的态度。他相信,AGI将帮助人类解决重大科学难题,通过帮助人类治疗疾病、开发清洁能源等方式提升人类社会生活质量。Hassabis描绘了一个梦幻的未来场景,“未来的AI将让我们彻底告别工作,尽情享乐,专注于探索生活的意义。”
以下是 Demis Hassabis 的播客内容,AI 科技评论作了不改原意的整理:
1 炒作还是低估
Hannah Fry:我想知道,现在公众对AI的兴趣激增,你的工作是更容易还是更困难?
Demis Hassabis:我认为这是一把双刃剑。我认为这更难,因为整个领域都有太多的审查、关注,而且还有很多噪音。其实,我更喜欢之前关注的人更少的时候,也许会更专注于科学。
但这也是好事,因为它表明该技术已经准备好以许多不同的方式影响现实世界,并以积极的方式影响人们的日常生活。所以我认为这也很令人兴奋。
Hannah Fry:您对这件事如此迅速地引起公众的想象力感到惊讶吗?我的意思是,我猜您预料到了人们最终会加入到AI行业。
Demis Hassabis:是的,完全正确,尤其是像我们这些一样致力于这个工作许多年,甚至几十年的人。所以我想在某个时候,公众会意识到这个事实。事实上,每个人都开始意识到AI有多重要。
但看到它真正实现并发生仍然是相当超现实的。我想这是因为聊天机器人和语言模型的出现。每个人都在使用语言,都能理解语言。因此,对于公众来说,这是一种简单的办法来理解并衡量人工智能的发展方向。
Hannah Fry:我想问你一些关于炒作的问题。你认为我们现在所处的位置,目前(AI)的情况是被夸大了还是低估了?或者它只是大肆宣传,也许方向上发生了错误。
Demis Hassabis:是的,我认为更多的是后者。所以我认为在短期内,这是过度炒作。人们声称可以做各种不能做的事情。有各种各样的初创公司和风险投资公司在追逐尚未准备好的疯狂的想法。
另一方面,我认为它仍然被低估了。我认为即使是现在认为它仍然被低估了,或者说甚至现在都还没有得到足够的重视。当我们进入AGI时代和后AGI时代会发生什么?我仍然觉得人们还不太了解这将会是多么的巨大(的一件事)。因此也没有理解其责任。
所以两者都有,真的。目前短期内它有点被夸大了,我们正在经历这个循环。
Hannah Fry:不过我想就所有这些潜在的初创公司和风险投资公司等而言,正如你所说,你在这些领域已经工作和生活了几十年,有足够的能力去辨别哪些初创公司有现实的目标,哪些不是。但是对其他人来说,他们要如何区分什么是真实的,什么是虚假的?
Demis Hassabis:我认为显然你必须进行完全的技术调查,对技术和最新趋势有一定的了解。
我认为也可以看看说这些话的人的背景,他们的技术背景如何,他们是从去年才加入AI领域的吗?可能他们去年在做加密货币。这些可能是他们在跟风追随潮流的一些线索。当然,这并不意味着他们不会有一些好的想法。
很多人都会这样做,但我们应该说,这更像是彩票。
我认为当一个地方突然受到大量关注时,这种情况总是会发生的,金钱也会随之而来。每个人都感觉自己错过了什么。这创造了一种机会主义的环境,这与我们这些几十年来一直专注于深度技术、深度科学的人相反。我认为这正是我们需要的理想方式,尤其是当我们越来越接近AGI时。
2 开源与AI 智能体的双刃剑
Hannah Fry:我想到的下一个问题是关于开源的。因为当事情掌握在人们手中时,正如你所提到的,真正非凡的事情可能会发生。我知道Deep Mind过去有很多开源项目,但现在随着我们的前进,这种情况似乎略有改变。所以请告诉我您对开源的立场。
Demis Hassabis:正如你所知,我是开源和开放科学的大力支持者。
我们已经放弃并发布了我们几乎所做的所有事情,包括transformers和AlphaGo之类的东西。我们在Nature和Science上发表了所有的东西。正如我们上次介绍的那样,AlphaGo是开源的。这是不错的选择,你会觉得它是绝对正确的。
这也是所有工作都能顺利进行的原因,因为通过共享信息,技术和科学才能尽快进步。所以,我们几乎总是这样做,这是一个普遍的好处。
科学就是这样运作的。例外的情况是,当你在面对AGI和强大的AI时(确实会陷入这种情况),就是当你拥有双重用途的技术时。你想要让所有的使用案例都从好的方向出发,所有真正的科学家都能善意地采取行动,让技术建立在想法之上,对想法进行批判等等。这样,这才是社会进步最快的方式。
但问题是,如何同时限制不良分子的访问权限,他们会拿走相同的系统,将它们重新用于不良目的,把它们滥用在武器系统等地方。这些通用系统可以像这样被重新调整用途。
现在还好,因为我认为现在的系统没有那么强大。但是在两到四年的时间里,特别是当你开始使用智能体系统或者用AI做一些行为时,那么我认为,如果它被某人或甚至是流氓国家滥用,可能会造成严重的伤害。而且我没有办法解决这个问题。
但作为一个社群,我们需要思考这对开源意味着什么?或许我们需要对前沿模型进行更多的检查,然后只有在它们发布一两年后,才能开源。
这就是我们正在遵循的模式,因为我们有自己的Gemini开放模型,名为Gemma。因为它们更小,所以它们不是前沿模型。它们的功能对开发人员仍然非常有用。因为它们有更少的参数数量,很容易在笔记本电脑上运行。虽然它们不是前沿模型,但它们只是不如最新的,Gemini 1.5那么强大。
所以我认为这可能是我们最终会采取的方法,我们将拥有开源模型,但它们会落后于最先进的模型,也许落后一年,这样我们就可以真正评估通过以下方式进行公开评估:用户了解这些模型可以做什么,前沿模型可以做什么。
Hannah Fry:我想你真的可以测试出随机的边界在哪里。
Demis Hassabis:是的,我们会看到边界在哪里。开源的问题是,如果出了问题,你就想不起来了。
而在闭源模型方面,如果你的操作者开始以不良方式用它,你只需要像关闭水龙头一样关闭它即可。在特殊情况下,你可以把它关闭。
但你一旦开源了某些东西,你就无法收回了。所以这是一个单向门。所以当你这样做时,你应该非常确定。
Hannah Fry:但是在一个模型中有包含AGI的可能性吗?
Demis Hassabis:这是一个完全独立的问题。我认为当你开始谈论强大的AGI级别的时候,我们现在不知道该怎么做。
Hannah Fry:那关于中间的过渡呢?
Demis Hassabis:关于这一点,我认为我们对于如何做到这一点有很好的想法。其中之一就是一个类似安全沙盒的东西。我想在游戏环境或尚未完全联网的互联网版本中测试智能体行为。在这个领域,我们可能会借鉴金融科技领域的理念,构建这类系统。
但是,我们也知道,这并不足以容纳 AGI(一种可能比我们更聪明的东西)。所以我认为我们必须更好地理解这些系统,这样才能为人工智能设计协议。到那时候,我们就会有更好的办法来控制它,也有可能使用AI和工具来监控下一版本的AI。
Hannah Fry:关于安全问题,我知道您是2023年由英国政府在布莱切利公园举行的AI安全峰会的重要参与者。从外界来看,我认为很多人只是在说监管这个词,就好像它会自己进来解决一切问题一样。但是你对于如何构建监管体系有什么看法?
Demis Hassabis:我认为各国政府加快参与其中的速度是件好事。
最近公众对AI的兴趣爆发的一个好处就是,政府正在关注这个话题,尤其是英国政府。我认为这很棒,我和他们谈过很多次,还有美国政府。他们的政府工作人员中有很多非常聪明的人,他们现在已经对这项技术了解得很清楚了。
我也很高兴看到英国和美国成立了人工智能安全机构,我认为许多其他国家也会效仿。我认为在AI风险变得非常高之前,这些都是我们需要遵守的很不错的先例和协议。
这也是一个证明的阶段。我认为国际合作确实是必要的,最好是围绕监管、安全护栏和部署规范等方面进行合作。
因为AI是一种数字技术,所以很难将它控制在国界内。当我们开始接近AGI时,我的观点是你必须这样做。因为技术变化如此之快,我们必须非常灵活和轻松地进行监管,以便适应最新技术的发展方向。
如果你在五年前对AI进行监管,你监管的东西与我们今天看到的完全不同。而且五年后可能会再次不同,这些基于智能体的系统可能是风险最高的系统。所以现在我建议加强已经存在的领域的现有法规,比如健康、交通等。
我认为可以像之前为互联网更新一样进行实时更新。同时,做一个像简报一样的东西,这也可能是我要做的第一件事情。简报用于确保人们能理解并测试前沿系统。
当人们对AI系统的使用变得更加清晰和明确时,就能更好地围绕这些行为对AI系统进行监管。
3 AI 智能体幻想成真?
Hannah Fry:你可以给我们概述一下什么是Grounding吗?
Demis Hassabis:Grounding是80年代和90年代在特斯拉和麻省理工学院建立经典的AI系统,一些大型逻辑系统,的原因之一。你可以把它想象成一个单词与其他单词关联的巨大语言库。
比如说,“狗有腿”就在这个库里面。但问题是,如果你给它展示了一张狗的图片,它根本不知道这些像素的集合指的是那个符号。这就是Grounding问题。
在语言库里面有一个象征的抽象表达,但是无法确定这个抽象的东西在现实世界真正意味着什么。人们尝试解决这个问题,但永远也无法做到完全正确的对应。
当然,现在的系统不是这样的,它直接从数据中学习,所以从某种程度上来说,现在的系统从一开始就建立了这种联系。
Hannah Fry:Astra计划,Google新的通用AI助手项目,可以接收视频和音频数据。之前你举了Astra帮你记住眼睛放在哪里的例子,所以我想知道这个产品的定位,是之前的Google眼镜的一个全新版本吗?
Demis Hassabis:当然,Google在开发眼镜型设备上有着悠久的历史,可以追溯到2012年,在这方面可以说是遥遥领先的,但他们只是缺少这样一种技术。
通过Astra,你能真正理解,一个AI 智能体或者说AI助手所看到的一切。所以我们对数字助理能够陪伴您并了解您周围的世界感到非常兴奋。当你使用它时,它真的能给你提供非常自然的体验。
Hannah Fry:大语言模型还有一段路要走,这些模型还不太擅长一些事情。
Demis Hassabis:是的。实际上这就是现在主要的争论。最新的这些模型其实是从五六年前发明的技术中诞生的。问题是,它们仍然有很多问题需要改进。我们都知道,大语言模型会产生幻觉,还不擅长做规划。
Hannah Fry:什么意义上的规划?
Demis Hassabis:长期规划。他们无法解决问题,尤其是一些长期的事情。如果你给它一个目标,它们其实无法真正为你在世界上采取行动。它们很像被动的问答系统。你向它提出问题,然后它会给你某种回应,但它们无法为你解决问题。
你可能会想象这样一个场景。你对AI助手说给我计划意大利的假期,预订好所有的餐馆和博物馆。它知道你喜欢什么,随后它就会帮你处理好机票等所有东西。
其实现在的AI助手做不到这样的事情。但我认为这是在下一个时代可以实现的,我称之为“基于智能体的系统”或“具有类似智能体行为的代理系统”。这是我们所擅长的东西。
这也是我们从过去做游戏智能体AlphaGo开始就一直想要做的事情,我们正在做的很多事情都是将这些我们出名的工作成果与新的多模态模型结合起来。我认为这将会是下一代系统,你可以把它看作是Alpha和Gemini的结合。
Hannah Fry:是的,我猜AlphaGo非常擅长做规划?
Demis Hassabis:没错,它非常擅长做规划,当然仅限于游戏领域。我们还需要把它推广到日常工作和语言的一般领域。
4 AGI的未来
Hannah Fry:在你描述的未来图景中,如果我们到了AGI的阶段,专注科学研究的机构还存在吗?
Demis Hassabis:我认为是的。在AGI阶段,社会、学术界、政府和工业实验室都会在一起合作进行研究。我认为这是我们到达最后阶段的唯一途径。如果是在AGI之后,我认为我们可以用它来回答一些物理学中的原理、现实的本质、意识等方面的最基本的问题。
Hannah Fry:你认识计算机科学家Stuart Russell吗?他告诉我他有点担心,一旦我们进入人工智能时代,我们可能会变得像过去的皇家王子一样,那些从来不需要登上王位或者做任何工作的人,只是过着肆无忌惮的奢华生活而没有任何目的。
Demis Hassabis:是的,这是一个有趣的问题。它超出了AGI的范围,更像是人们称之为ASI的超级AI。
那时候我们应该拥有彻底的富足。假设我们公平公正地分配这些资源,那么我们将有更多的自由来选择做什么。到那时候,意义将成为一个重大的哲学问题。我们需要哲学家,甚至是神学家,去思考这个问题。
回到我们之前说的炒作,我认为即使那些炒作也绝对低估了AI可能带来的转变。我认为在极限范围内会变得特别好。我们将会治愈许多疾病或者说所有的疾病,解决我们的能源问题、气候问题。
接下来的问题就只是,这有意义吗?
各位读者是否赞同Hassabis的观点呢?欢迎在评论区分享你对未来AI的设想~
参考资料:
如有侵犯您的版权,请及时联系3500663466#qq.com(#换@),我们将第一时间删除本站数据。














暂无评论内容