题目来源[BUUCTF]REVERSE——rsa
打开文件夹有两个文件
打开 pub.key 文件
复制到解密网站
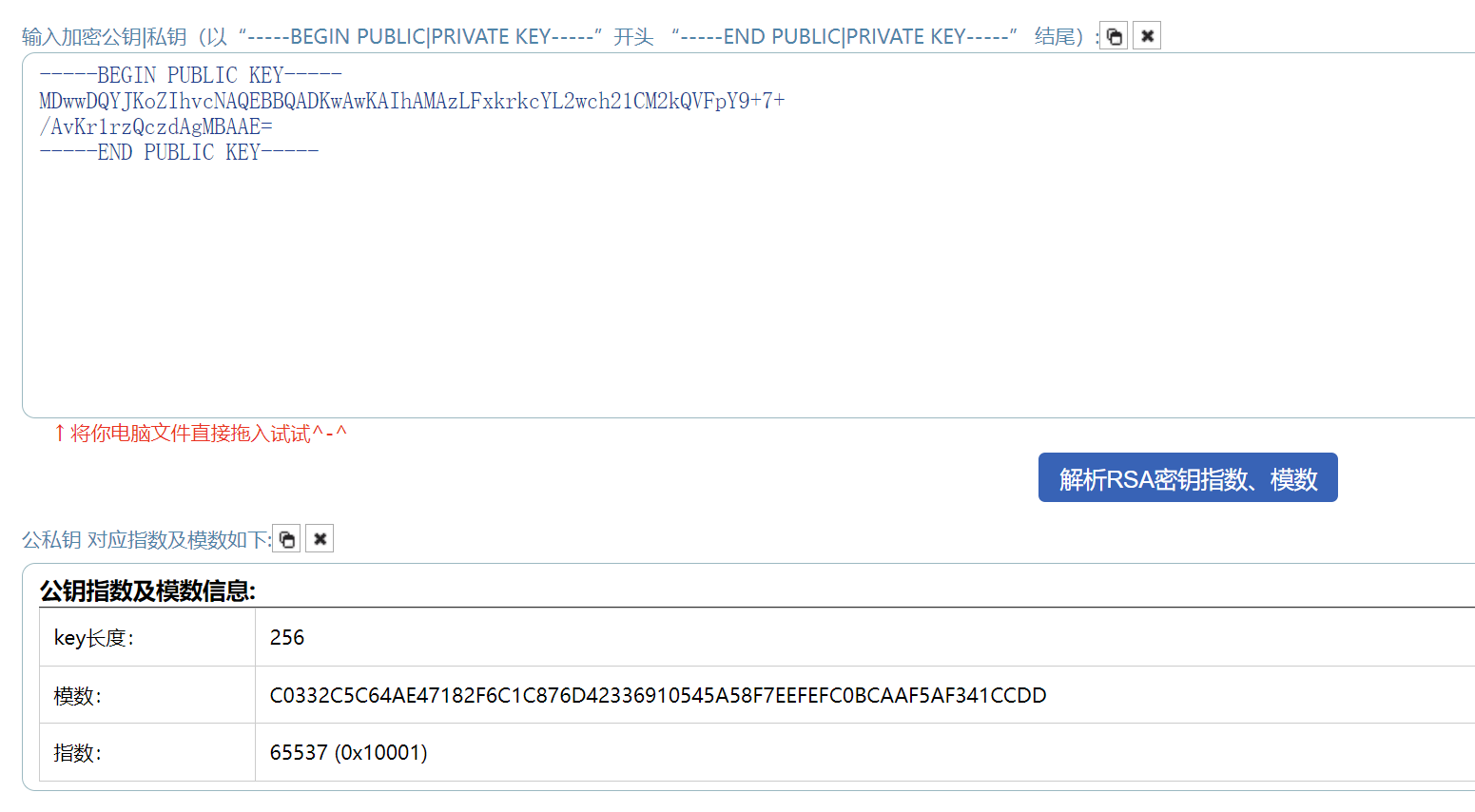
对应 RSA 密钥指数 E=65537,这一串模数可以转化为十进制后可以分离出 p、q
![图片[1]-RSA加密-后端开发牛翰社区-编程开发-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2024/08/5106583298973237132.png)
p=285960468890451637935629440372639283459,q=304008741604601924494328155975272418463
所以已知 E、p、q,也就已知 N、L,解密脚本
import gmpy2
import rsa
E = 65537
N = 86934482296048119190666062003494800588905656017203025617216654058378322103517
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463
pq = (p-1)*(q-1)
d = gmpy2.invert(E,pq)
key = rsa.PrivateKey(N, E, int(d), p, q)
with open("F:\\CTF question\\BUUCTF\\Reverse\\output\\flag.enc", "rb+") as f:
f = f.read() # 读取 flag.enc 内容并用 RSA 算法解密
print(rsa.decrypt(f, key))
flag{decrypt_256}
RSA 加密算法
加密:
密文 = 明文的E次方 mod N
公钥为 E、N 组合(E,N)
解密:
明文 = 密文的D次方 mod N
私钥为 D、N 组合 (D,N)
密钥对生成:
N: 两个质数 p、q 相乘 N = p*q
L: p-1、q-1 的最小公倍数 L = lcm(p-1,q-1)
E: 满足:1<E<L, E和L最大公约数为 1 1<E<L,gcd(E,L) = 1
D: 由 E 计算出 1<D<L,E*D mod L = 1










没有回复内容