手把手教你建【货币】一题的网络流模型

猿柒

18天前发布

现在已知如下问题，并告诉你这题可以用网络流来解决，你该怎么做，该怎么建出网络流的模型？

一些前提：

显然可以发现绝不可能走横向向左的边，但可能走竖向向上的边（如下图）

那么图其实就是这样的：问从 \(s\) 到 \(t\) 的最小花费

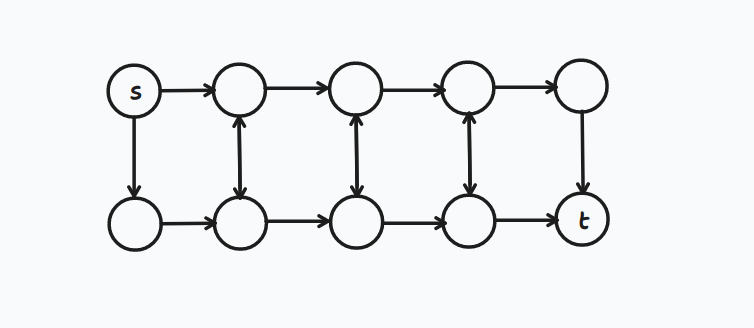
如果没有那 \(m\) 条限制，我们直接跑最短路就行了，加上这些限制，发现其实是个网络流模型，考虑如何建出网络流模型。

建模：

我们虚构出以下的模型以方便理解——很典的模型：对偶图！（具体什么是对偶图自行了解）

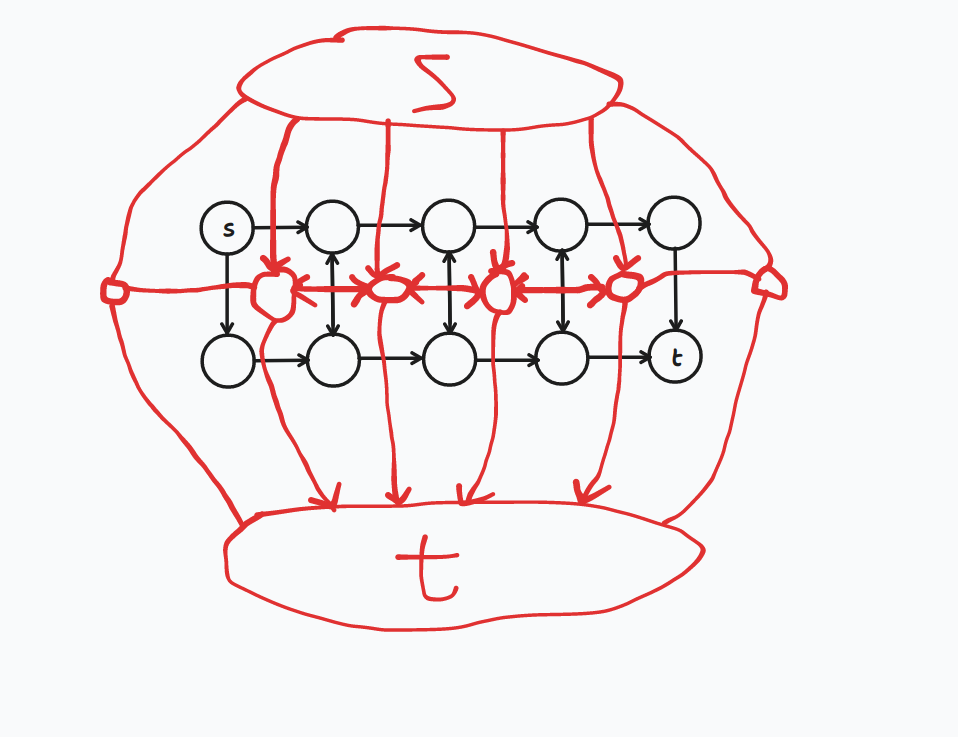
注：没方向的边是现在还不清楚该怎么建，稍后考虑。

每条红边（网络流上的边）的权值就是其交叉的黑边（实际的图）的权值

（好像个灯笼）现在实际上从 s 到 t 的最短花费其实就是 s 到 t 的红色连边构成的图的最小割了。

为什么？我们单独扣出来两个点证明一下：

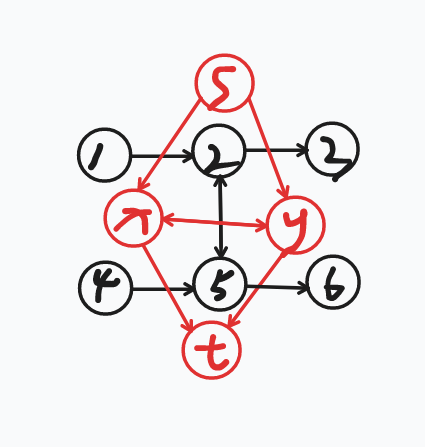
如上图，先不考虑横着的红边的话，根据最小割知识，我们知道在路径 \((s,x) 和 (x,t)\) 中必须要割掉一条且只割掉一条，同样，在 \((s,y) 和 (y, t)\) 中必须要割掉一条且只割掉一条，（必须割一条是为了满足没有增广路可以从 s 到 t ）；

为什么各只能割掉一条呢？

如果我们保证需要割 \((x,y)\) 这条边，则只会再割 \((s,y),(x,t)\)；不然无论是割 \((s,y),(s,x)\) 还是割 \((x,t),(y,t)\) 都会使得没有必要割 \((x,y)\)，与保证需要矛盾。
若割 \((y,x)\) 同理；
若既不割 \((x,y)\) 也不割 \((y,x)\)：
- 如果保证需要割掉 \((x,t)\)，那么需要割 \((y,t)\) 时不用再割别的边了，这不用解释。那如果我们割 \((s,y)\) 呢，这样仍然有增广路 s->x->y->t，此时因为我们既不割 \((x,y)\) 也不割 \((y,t)\)，所以必须割掉 \((s,x)\)，此时会发现 \((s,x) 和 (x,y)\) 都割掉了，那么 \((x,t)\) 是没必要割的，矛盾！
- 不割 \((x,t)\) 的话，同理。

对照实际的图，发现一样，如果走 1->2 这条边，一定不会走 4->5 这条边，走 2->3 一定不会走 5->6；

如果走了 2->5，那么要么是走 1->2->5->6，要么是走 4->5->2->3。

所以其实可以发现最小割就是原图中的最短路。

解决了以上问题，那么现在我们只需再解决 \(m\) 个限制条件和灯笼图中没有方向的红边（最左边和最右边点的边）两个问题即可。

如何解决 \(m\) 个限制？

还是扣出两个点，（只扣模型点了），如果题目限制同时走 s->x 和 y->t （x 和 y 并不一定相邻）时，需要再增加大小为 \(c\) 的花费。（现在暂时当作没有虚线边）

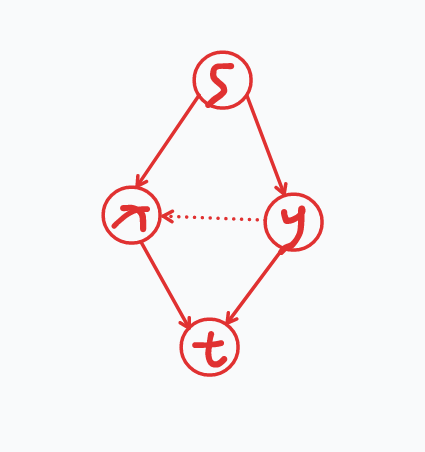
那么等同于我们需要考虑如何使得在既割 s->x 又割 y->t 的情况下，还需要再多割一条花费为 \(c\) 的边，我们再建一条从 y 到 x ，花费为 \(c\) 的边就解决了。（就是图中虚线边）。

显然割掉 s->x 和 y->t 后，还有一条增广路 s->y->x->t，所以必须再割掉 y->x，（上文已经证明出来此时不会再割 x->t 和 s->y ）。ok 了。

对于最左和最右那两个点的处理

现在把最右边那部分边拿出来，显然可以连成这样：

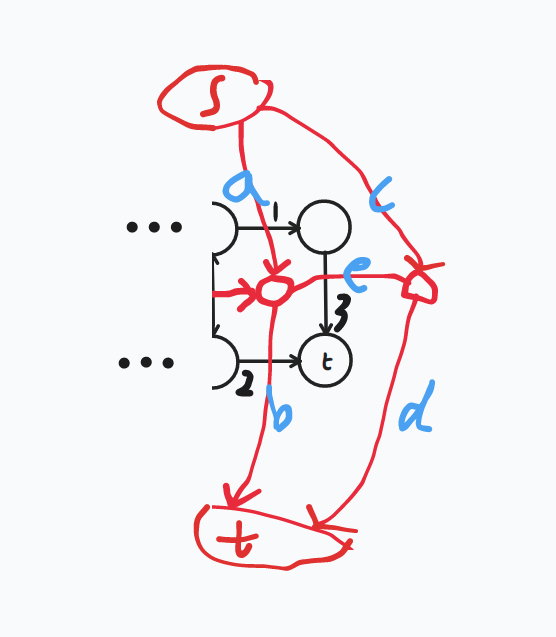
可以发现，在 1、2 边之间（显然这两条边只能走一个）如果我们走的是 2，则没什么事；但如果走的是 1 这条边，那么就一定要走 3 这条边。考虑在网络流上怎么解决？

意思就是需要在 a、b 之间选择割 a 这条边的时候，必须要再割掉 e 这条边。

其实把 d 权值附为 0，c 附为 inf，然后 e 从右边那个点连向左边那个即可，这样保证割 d 不割 c，此时若割 a，则还需要割掉 e 以使增广路 c-e-b 不再增广。

如下图：

\[e \]

\[@<–@ \]

什么，你要看代码？还是自己写吧

#include <bits/stdc++.h>
#define int long long
typedef long long ll;
using namespace std;

const int N = 1e4 + 10;
const ll inf = 20071120100000000;

int n, m, s, t;
ll dis[N], ans; int now[N];

int tot=1, head[N], to[N<<1], nxt[N<<1]; ll w[N<<1];
inline void add(int x, int y, ll z){
    w[++tot] = z, w[tot+1] = 0;
    to[tot] = y, to[tot+1] = x;
    nxt[tot] = head[x], nxt[tot+1] = head[y];
    head[x] = tot++, head[y] = tot;
}

inline int bfs(){
    for(int i=0; i<=n+2; i++) dis[i] = inf;
    queue<int>q; q.push(s);
    dis[s] = 0, now[s] = head[s];

    while(q.size())
    {
        int x = q.front(); q.pop();
        for(int i=head[x]; i; i=nxt[i]){
            int y = to[i]; 
            if(w[i] > 0 and dis[y] == inf){
                dis[y] = dis[x] + 1;
                q.push(y); now[y] = head[y];
                if(y == t) return 1;
            }
        }   
    }
    return 0;
}

inline int dfs(int x, ll sum){
    if(x == t) return sum;
    ll k = 0, res = 0;
    for(int i=now[x]; i&&sum; i=nxt[i]){
        now[x] = i; int y = to[i];
        if(w[i] > 0 and dis[y] == dis[x] + 1){
            k = dfs(y, min(sum, w[i]));
            if(k == 0) dis[y] = inf;
            w[i] -= k, w[i^1] += k;
            res += k, sum -= k;
        }
    }
    return res;
}

signed main(){ //currency
    freopen("currency.in", "r", stdin), freopen("currency.out", "w", stdout);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin>>n>>m; s = n + 1, t = n + 2; int x;
    for(int i=1; i<n; i++) cin>>x, add(s, i, x);
    for(int i=1; i<=n; i++){
        cin>>x; add(i, i-1, x);
        if(i != 1 and i != n) add(i-1, i, x);
    }
    for(int i=1; i<n; i++) cin>>x, add(i, t, x);
    for(int i=1; i<=m; i++){
        int y, z; cin>>x>>y>>z;
        add(y, x, z);
    }add(s, 0, 0), add(0, t, inf); add(s, n, inf), add(n, t, 0);

    while(bfs()) ans += dfs(s, inf);

    cout<<ans<<"\n";


    return 0;
}

评分

欢迎为Ta评分