Codeforces Rund 976 div2 个人题解(A~E)
Dashboard – Codeforces Round 976 (Div. 2) and Divide By Zero 9.0 – Codeforces
火车头
#define _CRT_SECURE_NO_WARNINGS 1
#include <algorithm>
#include <array>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <fstream>
#include <functional>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <list>
#include <map>
#include <numeric>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <string>
#include <tuple>
#include <unordered_map>
#include <utility>
#include <vector>
#define ft first
#define sd second
#define yes cout << "yes\n"
#define no cout << "no\n"
#define Yes cout << "Yes\n"
#define No cout << "No\n"
#define YES cout << "YES\n"
#define NO cout << "NO\n"
#define pb push_back
#define eb emplace_back
#define all(x) x.begin(), x.end()
#define all1(x) x.begin() + 1, x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define unq_all1(x) x.erase(unique(all1(x)), x.end())
#define sort_all(x) sort(all(x))
#define sort1_all(x) sort(all1(x))
#define reverse_all(x) reverse(all(x))
#define reverse1_all(x) reverse(all1(x))
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fLL
#define RED cout << "\033[91m"
#define GREEN cout << "\033[92m"
#define YELLOW cout << "\033[93m"
#define BLUE cout << "\033[94m"
#define MAGENTA cout << "\033[95m"
#define CYAN cout << "\033[96m"
#define RESET cout << "\033[0m"
// 红色
#define DEBUG1(x) \
RED; \
cout << #x << " : " << x << endl; \
RESET;
// 绿色
#define DEBUG2(x) \
GREEN; \
cout << #x << " : " << x << endl; \
RESET;
// 蓝色
#define DEBUG3(x) \
BLUE; \
cout << #x << " : " << x << endl; \
RESET;
// 品红
#define DEBUG4(x) \
MAGENTA; \
cout << #x << " : " << x << endl; \
RESET;
// 青色
#define DEBUG5(x) \
CYAN; \
cout << #x << " : " << x << endl; \
RESET;
// 黄色
#define DEBUG6(x) \
YELLOW; \
cout << #x << " : " << x << endl; \
RESET;
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
// typedef __int128_t i128;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<ll, int> pli;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;
typedef tuple<int, int, int> ti3;
typedef tuple<ll, ll, ll> tl3;
typedef tuple<ld, ld, ld> tld3;
typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pli> vpli;
typedef vector<pss> vpss;
typedef vector<ti3> vti3;
typedef vector<tl3> vtl3;
typedef vector<tld3> vtld3;
typedef vector<vi> vvi;
typedef vector<vl> vvl;
typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;
typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;
typedef priority_queue<string> pqs;
typedef priority_queue<pii> pqpii;
typedef priority_queue<psi> pqpsi;
typedef priority_queue<pll> pqpll;
typedef priority_queue<psi> pqpsl;
typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;
typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;
std::mt19937_64 rng(std::chrono::steady_clock::now().time_since_epoch().count());
template <typename T>
inline T read()
{
T x = 0;
int y = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
y = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * y;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
putchar('-');
x = -x;
}
if (x >= 10)
{
write(x / 10);
}
putchar(x % 10 + '0');
}
/*#####################################BEGIN#####################################*/
void solve()
{
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
// freopen("test.in", "r", stdin);
// freopen("test.out", "w", stdout);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
/*######################################END######################################*/
// 链接:
A. Find Minimum Operations
每个测试的时间限制:1秒
每个测试的内存限制:256兆字节
输入:标准输入
输出:标准输出
给定两个整数\(n\)和\(k\)。
在一次操作中,你可以从\(n\)中减去任何\(k\)的幂。具体来说,在一次操作中,你可以将\(n\)替换为\((n – k^x)\),其中\(x\)是非负整数。
找出将\(n\)变为\(0\)所需的最小操作次数。
输入
每个测试包含多个测试用例。第一行是测试用例的数量\(t\)(\(1 \le t \le 10^4\))。后面是每个测试用例的描述。
每个测试用例的唯一一行包含两个整数\(n\)和\(k\)(\(1 \le n, k \le 10^9\))。
输出
对于每个测试用例,输出每行所需的最小操作次数。
示例
输入
6
5 2
3 5
16 4
100 3
6492 10
10 1
输出
2
3
1
4
21
10
注意
在第一个测试用例中,\(n = 5\)和\(k = 2\)。我们可以执行以下操作序列:
- 从\(5\)中减去\(2^0 = 1\),当前值变为\(5 – 1 = 4\)。
- 从\(4\)中减去\(2^2 = 4\),当前值变为\(4 – 4 = 0\)。
可以证明在少于\(2\)次操作的情况下无法将\(n\)变为\(0\)。因此,答案是\(2\)。
在第二个测试用例中,\(n = 3\)和\(k = 5\)。我们可以执行以下操作序列:
- 从\(3\)中减去\(5^0 = 1\),当前值变为\(3 – 1 = 2\)。
- 从\(2\)中减去\(5^0 = 1\),当前值变为\(2 – 1 = 1\)。
- 从\(1\)中减去\(5^0 = 1\),当前值变为\(1 – 1 = 0\)。
可以证明在少于\(3\)次操作的情况下无法将\(n\)变为\(0\)。因此,答案是\(3\)。
解题思路
-
特殊情况处理:
- 当\(k = 1\)时,我们只能减去\(1\)(即\(1^0\)),因此将\(n\)减到\(0\)需要\(n\)次操作。
-
计算\(k\)的幂:
- 对于\(k > 1\),我们需要计算出所有可能的\(k^x\)(直到\(k^x\)超过\(10^9\)),并将这些值存储在一个列表中。
-
贪心算法:
- 从最大的\(k^x\)开始,优先使用较大的幂来减少\(n\),每次减去\(k^x\)的最大倍数,直到无法再减去为止。
- 继续使用下一个较小的\(k^x\),直到\(n\)减到\(0\)。
-
输出结果:
- 对于每个测试用例,输出所需的最小操作次数。
代码实现
void solve()
{
ll n, k; // 定义变量 n 和 k
cin >> n >> k; // 输入 n 和 k
if (k == 1) // 特殊情况处理
{
cout << n << endl; // 当 k 为 1 时,操作次数为 n
return; // 结束函数
}
vl v; // 定义一个列表 v 用于存储 k 的幂
v.pb(1); // 初始化列表,添加 k^0 = 1
for (ll i = 1; v.back() <= 1e9; i++) // 计算 k 的幂,直到超过 10^9
{
v.pb(v.back() * k); // 将下一个 k 的幂添加到列表中
}
ll ans = 0; // 初始化操作次数为 0
for (int i = v.size() - 1; i >= 0; i--) // 从最大的 k 的幂开始
{
ll t = v[i]; // 当前的 k 的幂
if (n >= t) // 如果 n 大于等于当前的 k 的幂
{
ans += n / t; // 计算可以减去多少次当前的 k 的幂
n %= t; // 更新 n,减去已使用的部分
}
}
cout << ans << endl; // 输出所需的最小操作次数
}
B. Brightness Begins
每个测试的时间限制:1秒
每个测试的内存限制:256兆字节
输入:标准输入
输出:标准输出
想象一下你有\(n\)个灯泡,编号为\(1, 2, \ldots, n\)。最初,所有灯泡都是开启的。翻转一个灯泡的状态意味着如果它是开启的,就将其关闭;如果它是关闭的,就将其开启。
接下来,你将执行以下操作:
- 对于每个\(i = 1, 2, \ldots, n\),翻转所有\(j\)的状态,其中\(j\)是\(i^\dagger\)的倍数。
执行完所有操作后,将会有几个灯泡仍然是开启的。你的目标是使这些灯泡的数量恰好为\(k\)。
找出满足条件的最小\(n\),使得在执行操作后正好有\(k\)个灯泡开启。我们可以证明总是存在答案。
\(^\dagger\)整数\(x\)被\(y\)整除,当且仅当存在一个整数\(z\),使得\(x = y \cdot z\)。
输入
每个测试包含多个测试用例。第一行是测试用例的数量\(t\)(\(1 \le t \le 10^4\))。后面是每个测试用例的描述。
每个测试用例的唯一一行包含一个整数\(k\)(\(1 \le k \le 10^{18}\))。
输出
对于每个测试用例,输出\(n\)— 最小的灯泡数量。
示例
输入
3
1
3
8
输出
2
5
11
注意
在第一个测试用例中,最小的灯泡数量是\(2\)。我们用数组表示所有灯泡的状态,其中\(1\)表示开启,\(0\)表示关闭。最初,数组为\([1, 1]\)。
- 执行\(i = 1\)的操作后,数组变为\([\underline{0}, \underline{0}]\)。
- 执行\(i = 2\)的操作后,数组变为\([0, \underline{1}]\)。
最后,开启的灯泡数量为\(k = 1\)。我们还可以证明答案不能小于\(2\)。
在第二个测试用例中,最小的灯泡数量是\(5\)。最初,数组为\([1, 1, 1, 1, 1]\)。
- 执行\(i = 1\)的操作后,数组变为\([\underline{0}, \underline{0}, \underline{0}, \underline{0}, \underline{0}]\)。
- 执行\(i = 2\)的操作后,数组变为\([0, \underline{1}, 0, \underline{1}, 0]\)。
- 执行\(i = 3\)的操作后,数组变为\([0, 1, \underline{1}, 1, 0]\)。
- 执行\(i = 4\)的操作后,数组变为\([0, 1, 1, \underline{0}, 0]\)。
- 执行\(i = 5\)的操作后,数组变为\([0, 1, 1, 0, \underline{1}]\)。
最后,开启的灯泡数量为\(k = 3\)。我们还可以证明答案不能小于\(5\)。
解题思路
-
灯泡状态翻转:
- 每个灯泡的状态在每次操作中会被翻转。具体来说,灯泡\(j\)在操作\(i\)时被翻转当且仅当\(j\)是\(i\)的倍数。
- 经过所有操作后,灯泡\(j\)的状态最终取决于\(j\)的因子数量。具体地,若\(j\)的因子数量为奇数,则灯泡\(j\)将处于开启状态;若为偶数,则灯泡\(j\)将处于关闭状态。
-
完全平方数的性质:
- 只有完全平方数的因子数量是奇数。因此,开启的灯泡数量等于小于或等于\(n\)的完全平方数的数量。
- 设\(m\)为小于或等于\(n\)的最大完全平方数的平方根,则开启的灯泡数量为\(m\)。
-
确定\(n\):
- 我们需要找到最小的\(n\),使得小于或等于\(n\)的完全平方数的数量\(m\)等于\(k\)。
- 这意味着我们需要满足\(m = k\),所以\(n\)应该是\(m^2\)和\(m^2 + 2m\)之间的值。
通过以上分析,我们可以使用二分查找来快速找到满足条件的最小\(n\)。
代码实现
ll floor_sqrt(ll n)
{
ll res = sqrt((ld)n); // 计算 n 的平方根的整数部分
while ((res + 1) * (res + 1) <= n) // 确保 res 是最大的整数,使得 res^2 <= n
res++;
while (res * res > n) // 确保 res 是最小的整数,使得 res^2 <= n
res--;
return res; // 返回 n 的整数平方根
}
void solve()
{
ll k; // 声明变量 k
cin >> k; // 读取输入的 k
ll l = k; // 二分查找的左边界
ll r = k + inf; // 二分查找的右边界,inf 是一个足够大的数
ll ans = -1; // 初始化答案为 -1
while (l < r) // 当左边界小于右边界时继续循环
{
ll mid = (l + r) / 2; // 计算中间值 mid
ll sqr = floor_sqrt(mid); // 计算 mid 的平方根
ll diff = mid - sqr; // 计算 mid 与其平方根的差值
if (diff < k) // 如果差值小于 k,说明需要更大的 n
l = mid + 1;
else
r = mid;
}
cout << l << "\n"; // 输出结果
}
C. Bitwise Balancing
每个测试的时间限制:2秒
每个测试的内存限制:256兆字节
输入:标准输入
输出:标准输出
给定三个非负整数\(b\),\(c\), 和\(d\)。
请找到一个非负整数\(a\),使得\((a | b) – (a \& c) = d\),其中\(|\)和 & 分别表示按位或操作和按位与操作。
如果这样的\(a\)存在,输出它的值。如果没有解,输出整数\(-1\)。如果有多个解,输出任意一个。
输入
每个测试包含多个测试用例。第一行是测试用例的数量\(t\)(\(1 \le t \le 10^5\))。后面是每个测试用例的描述。
每个测试用例的唯一一行包含三个正整数\(b\),\(c\), 和\(d\)(\(0 \le b, c, d \le 10^{18}\))。
输出
对于每个测试用例,输出\(a\)的值,或者\(-1\)如果没有解决方案。
示例
输入
3
2 2 2
4 2 6
10 2 14
输出
0
-1
12
注意
在第一个测试用例中,\((0\,|\,2)-(0\,\&\,2)=2-0=2\)。因此,\(a = 0\)是一个正确答案。
在第二个测试用例中,没有任何值的\(a\)满足该方程。
在第三个测试用例中,\((12\,|\,10)-(12\,\&\,2)=14-0=14\)。因此,\(a = 12\)是一个正确答案。
解题思路
-
按位操作分析:
- 通过分析按位或和按位与的性质,我们可以将问题转化为逐位处理。
- 对于每一位\(i\),我们将\(b\),\(c\), 和\(d\)的第\(i\)位分别表示为\(\text{dig}_b\),\(\text{dig}_c\), 和\(\text{dig}_d\)。
- 我们需要决定\(a\)的第\(i\)位\(a_i\)是 0 还是 1,以满足上述等式。
-
状态转移:
- 根据\(a_i\)的取值(0 或 1),我们可以计算出\((a_i | \text{dig}_b)\)和\((a_i \& \text{dig}_c)\)的值,并通过这些值计算出当前位的差异。
- 通过维护一个进位\(\text{dig}\),我们可以有效地处理每一位的状态。
-
条件判断:
- 在每一位的处理过程中,我们需要检查是否存在合适的\(a_i\)使得条件成立。
- 如果在任何一位无法找到合适的\(a_i\),则该测试用例返回\(-1\)。
代码实现
const int N = 64; // 定义位数为64位
void solve()
{
ll _b, _c, _d;
cin >> _b >> _c >> _d;
bitset<N> b(_b);
bitset<N> c(_c);
bitset<N> d(_d);
bitset<N> a;
int dig = 0; // 初始化进位
bool flag1 = true; // 标记是否找到解
// 遍历每一位
for (int i = 0; i < N; ++i)
{
int dig_b = b[i]; // 读取 b 的第 i 位
int dig_c = c[i]; // 读取 c 的第 i 位
int dig_d = d[i]; // 读取 d 的第 i 位
bool flag2 = false; // 标记是否找到当前位的解
// 尝试 a_i 为 0 或 1
for (int a_i = 0; a_i <= 1; ++a_i)
{
int or_d = a_i | dig_b; // 计算当前位的或结果
int and_d = a_i & dig_c; // 计算当前位的与结果
int diff_d = or_d - and_d; // 计算差值
int tot = diff_d + dig; // 计算总和
// 检查条件
if (tot < dig_d)
continue; // 如果总和小于 dig_d,继续
if ((tot - dig_d) % 2 != 0)
continue; // 如果差值不是偶数,继续
int t = (tot - dig_d) / 2; // 计算进位
if (t < 0 || t > 1)
continue; // 如果进位不合法,继续
if (a_i == 1)
a.set(i); // 设置 a 的第 i 位
dig = t; // 更新进位
flag2 = true; // 找到当前位的解
break; // 退出循环
}
// 如果当前位没有解,设置标记为 false
if (!flag2)
{
flag1 = false;
break; // 退出位循环
}
}
// 检查最终进位是否为 0
if (dig != 0)
flag1 = false;
// 输出结果
if (flag1)
{
ll ans = 0; // 初始化答案
for (int i = 0; i < N; ++i)
{
if (a[i]) // 如果 a 的第 i 位为 1
{
ans |= (1LL << i); // 更新答案
}
}
cout << ans << "\n"; // 输出答案
}
else
cout << "-1\n"; // 输出 -1
}
D. Connect the Dots
每个测试的时间限制:2秒
每个测试的内存限制:512兆字节
输入:标准输入
输出:标准输出
在一个美好的傍晚,爱丽丝坐下来玩经典游戏“连接点”,但这次有些变化。
为了玩这个游戏,爱丽丝在一条直线上标记了\(n\)个点,索引从\(1\)到\(n\)。最初,这些点之间没有任何连接,因此它们都是分开的。之后,爱丽丝执行了\(m\)次操作,每次操作如下:
- 她选择三个整数\(a_i\),\(d_i\)(\(1 \le d_i \le 10\)),和\(k_i\)。
- 她选择点\(a_i, a_i + d_i, a_i + 2d_i, a_i + 3d_i, \ldots, a_i + k_i \cdot d_i\),并用弧连接这些点之间的每一对。
执行完所有\(m\)次操作后,她想知道这些点形成了多少个联通块\(^\dagger\)。请帮助她找到这个数量。
\(^\dagger\)如果两个点之间通过多个(可能为零)弧和其他点存在路径,则认为它们在一个联通块中。
输入
每个测试包含多个测试用例。第一行是测试用例的数量\(t\)(\(1 \le t \le 10^5\))。后面是每个测试用例的描述。
每个测试用例的第一行包含两个整数\(n\)和\(m\)(\(1 \le n \le 2 \cdot 10^5, 1 \le m \le 2 \cdot 10^5\))。
接下来的\(m\)行,每行包含三个整数\(a_i\),\(d_i\), 和\(k_i\)(\(1 \le a_i \le a_i + k_i \cdot d_i \le n, 1 \le d_i \le 10, 0 \le k_i \le n\))。
保证所有测试用例中\(n\)和\(m\)的总和不超过\(2 \cdot 10^5\)。
输出
对于每个测试用例,输出联通块的数量。
示例
输入
3
10 2
1 2 4
2 2 4
100 1
19 2 4
100 3
1 2 5
7 2 6
17 2 31
输出
2
96
61
注意
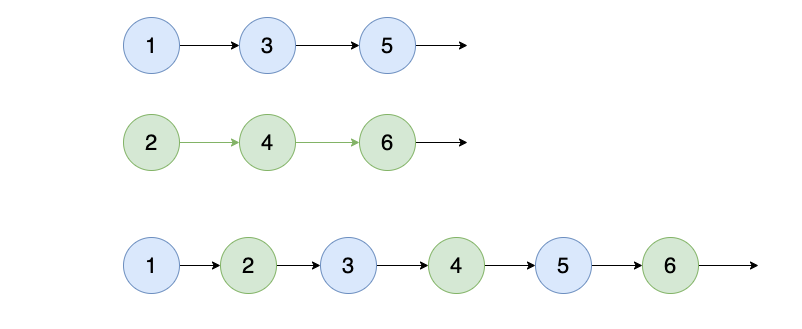
在第一个测试用例中,\(n = 10\)。第一次操作连接了点\(1\),\(3\),\(5\),\(7\), 和\(9\)。第二次操作连接了点\(2\),\(4\),\(6\),\(8\), 和\(10\)。因此有两个联通块:\(\{1, 3, 5, 7, 9\}\)和\(\{2, 4, 6, 8, 10\}\)。
在第二个测试用例中,\(n = 100\)。唯一的操作连接了点\(19\),\(21\),\(23\),\(25\), 和\(27\)。现在它们形成一个大小为\(5\)的联通块。其他\(95\)个点形成单点联通块。因此,答案是\(1 + 95 = 96\)。
在第三个测试用例中,\(n = 100\)。经过操作,所有从\(1\)到\(79\)的奇数点将形成一个大小为\(40\)的联通块。其他\(60\)个点形成单点联通块。因此,答案是\(1 + 60 = 61\)。
解题思路
注意到\(d<=10\),所以最多只有\(10×10=100\)种操作状态\((10种起始点×10种步长)\),所以我们可以把所有操作离线出来并进行分类。
我们可以将每个操作视为一个线段,左边界为起始点\(a_i\),右边界为\(a_i + k_i \cdot d_i\),然后对同一类的操作进行线段合并。先对线段集按照左边界排序,如果下一个线段的右边界小于等于左边界,就就把它合并进来。
经过这些操作,我们可以大幅度减少操作次数。每一类中单次操作次数越多越容易和别的操作合并,最后均摊下来每种类型的操作次数为\(\frac{n}{d}\),\(d\)为这一类操作的步长。
总和时间复杂度大概为\(T(100\times \frac{m}{100}\log\frac{m}{100}+m)\)
代码实现
struct DSU
{
vector<int> parent; // 父节点数组
vector<int> rank; // 秩(树的高度)
// 构造函数,初始化父节点和秩
DSU(int n) : parent(n + 1), rank(n + 1, 1)
{ // 点的编号从1到n
for (int i = 1; i <= n; ++i)
{
parent[i] = i; // 初始时每个点的父节点是它自己
}
}
// 查找根节点,带路径压缩
int find_set(int x)
{
if (parent[x] != x)
parent[x] = find_set(parent[x]); // 递归查找并进行路径压缩
return parent[x];
}
// 合并两个集合,按秩合并
void union_set(int x, int y)
{
int fx = find_set(x); // 查找x的根节点
int fy = find_set(y); // 查找y的根节点
if (fx == fy)
return; // 已经在同一个集合中
if (rank[fx] < rank[fy])
{
parent[fx] = fy; // 将fx的父节点设为fy
}
else
{
parent[fy] = fx; // 将fy的父节点设为fx
if (rank[fx] == rank[fy])
rank[fx]++; // 若秩相同,则fx的秩加1
}
}
};
#define l first
#define r second
void solve()
{
int n, m;
cin >> n >> m;
DSU dsu(n); // 初始化并查集
vector<vector<vpii>> opts(11, vector<vpii>(10, vpii())); // 存储操作的线段
for (int i = 0; i < m; ++i)
{
int a, d, k;
cin >> a >> d >> k;
int r = a % d; // 计算余数
opts[d][r].pb({a, a + k * d}); // 将操作存入对应的线段
}
for (int i = 1; i <= 10; ++i)
{
for (int j = 0; j < 10; ++j)
{
if (opts[i][j].size() < 2)
continue; // 如果线段少于2个,则跳过
sort(all(opts[i][j])); // 按左边界排序
int sz = opts[i][j].size();
vpii temp;
temp.eb(opts[i][j][0].l, opts[i][j][0].r); // 初始化第一个线段
for (int k = 1; k < sz; k++)
{
// 合并重叠的线段
if (temp.back().r < opts[i][j][k].l)
temp.eb(opts[i][j][k].l, opts[i][j][k].r);
else
temp.back().r = max(temp.back().r, opts[i][j][k].r);
}
opts[i][j] = temp; // 更新合并后的线段
}
}
for (int i = 1; i <= 10; ++i)
{
for (int j = 0; j < 10; ++j)
{
for (auto &[l, r] : opts[i][j])
{
// 对每个合并后的线段进行连接
for (int k = l; k + i <= min(n, r); k += i)
{
dsu.union_set(k, k + i); // 合并相邻的点
}
}
}
}
set<int> st; // 用于存储不同的根节点
for (int i = 1; i <= n; ++i)
{
st.insert(dsu.find_set(i)); // 查找每个点的根节点并存入集合
}
cout << st.size() << '\n'; // 输出联通块的数量
}
E. Expected Power
每个测试的时间限制:4秒
每个测试的内存限制:256兆字节
输入:标准输入
输出:标准输出
给定一个数组\(n\)整数\(a_1,a_2,\ldots,a_n\),以及一个数组\(p_1, p_2, \ldots, p_n\)。
设\(S\)为随机 多重集(即可能包含相同元素),构造过程如下:
- 初始时\(S\)是空的。
- 对于每个\(i\)从\(1\)到\(n\),以概率\(\frac{p_i}{10^4}\)将\(a_i\)插入\(S\)。请注意,每个元素是独立插入的。
定义\(f(S)\)为所有\(S\)元素的 按位异或。请计算\((f(S))^2\)的期望值,并输出答案模\(10^9 + 7\)。
形式上,设\(M = 10^9 + 7\)。可以证明答案可以表示为一个不可约分数\(\frac{p}{q}\),其中\(p\)和\(q\)是整数且\(q \not \equiv 0 \pmod{M}\)。输出等于\(p \cdot q^{-1} \bmod M\)的整数。换句话说,输出一个整数\(x\)使得\(0 \le x \le M\)且\(x \cdot q \equiv p \pmod{M}\)。
输入
每个测试包含多个测试用例。第一行是测试用例的数量\(t\)(\(1 \le t \le 10^4\))。后面是每个测试用例的描述。
每个测试用例的第一行包含一个整数\(n\)(\(1 \le n \le 2 \cdot 10^5\))。
第二行包含\(n\)个整数\(a_1,a_2,\ldots,a_n\)(\(1 \le a_i \le 1023\))。
第三行包含\(n\)个整数\(p_1,p_2,\ldots,p_n\)(\(1 \le p_i \le 10^4\))。
保证所有测试用例中\(n\)的总和不超过\(2 \cdot 10^5\)。
输出
对于每个测试用例,输出期望值\((f(S))^2\)的结果,模\(10^9 + 7\)。
示例
输入
4
2
1 2
5000 5000
2
1 1
1000 2000
6
343 624 675 451 902 820
6536 5326 7648 2165 9430 5428
1
1
10000
输出
500000007
820000006
280120536
注意
在第一个测试用例中,\(a = [1, 2]\),每个元素以概率\(\frac{1}{2}\)插入到\(S\),因此\(S\)有\(4\)种可能的结果,每种结果的概率为\(\frac{1}{4}\):
- \(S = \varnothing\),则\(f(S) = 0\),\((f(S))^2 = 0\)。
- \(S = \{1\}\),则\(f(S) = 1\),\((f(S))^2 = 1\)。
- \(S = \{2\}\),则\(f(S) = 2\),\((f(S))^2 = 4\)。
- \(S = \{1,2\}\),则\(f(S) = 1 \oplus 2 = 3\),\((f(S))^2 = 9\)。
因此答案为\(0 \cdot \frac{1}{4} + 1 \cdot \frac{1}{4} + 4 \cdot \frac{1}{4} + 9 \cdot \frac{1}{4} = \frac{14}{4} = \frac{7}{2} \equiv 500\,000\,007 \pmod{10^9 + 7}\)。
在第二个测试用例中,\(a = [1, 1]\),\(a_1\)以概率\(0.1\)插入\(S\),而\(a_2\)以概率\(0.2\)插入\(S\)。\(S\)有\(3\)种可能的结果:
- \(S = \varnothing\),则\(f(S) = 0\),\((f(S))^2 = 0\),概率为\(0.72\)。
- \(S = \{1\}\),则\(f(S) = 1\),\((f(S))^2 = 1\),概率为\(0.26\)。
- \(S = \{1, 1\}\),则\(f(S) = 0\),\((f(S))^2 = 0\),概率为\(0.02\)。
因此答案为\(0 \cdot 0.72 + 1 \cdot 0.26 + 0 \cdot 0.02 = 0.26 = \frac{26}{100} \equiv 820\,000\,006 \pmod{10^9 + 7}\)。
解题思路
题目大意
给定一个整数数组\(a_1, a_2, \ldots, a_n ,a_i\le 1023\)和概率数组\(p_1, p_2, \ldots, p_n\),每个元素\(a_i\)有概率\(\frac{p_i}{10^4}\)被选入集合\(S\)。集合\(S\)是一个多重集,允许有重复元素。定义\(f(S)\)为集合\(S\)中所有元素的按位异或(XOR)值。需要计算\(E[(f(S))^2]\)的期望值,并在\(10^9 + 7\)下取模。
推导过程
为了计算\(E[(f(S))^2]\),我们可以利用期望的线性性质,将其展开为不同\(x\)值的概率加权和:
\[E[(f(S))^2] = \sum_{x=0}^{1023} x^2 \cdot P(f(S) = x) \]
其中,\(P(f(S) = x)\)表示集合\(S\)中元素异或结果为\(x\)的概率。由于\(a_i \leq 1023\),异或结果\(x\)的范围为\([0, 1023]\)。
状态转移推导
注意到\(x\)的范围比较小,所以我们可以用子序列类\(dp\)的思想暴力枚举所有状态并进行状态转移来计算\(P(f(S) = x)\),时间复杂度为\(1024\times n\)。
我们定义\(f_{i,x}\)为在前\(i\)个元素中,\(S\)异或和为\(x\)的概率。
易推得状态转移方程
\[f_{i,x}=f_{i-1,x}+(1-p_i)\times f_{i-1,x},(不选a_i) \]
\[f_{i,x}=f_{i-1,x} +p_i\times f_{i-1,x \otimes{a_i}},(选a_i) \]
由于\(f_i\)只能由\(f_{i-1}\)转移过来,所以我们可以压缩掉一个储存空间
期望的计算
当\(f[x]\)确定后,期望\(E[(f(S))^2]\)就可以通过以下公式计算:
\[E[(f(S))^2] = \sum_{x=0}^{1023} x^2 \cdot f[x] \]
代码实现
const ll MOD = 1e9 + 7;
// 快速幂函数,用于计算模反元素
ll qmi(ll x, ll k, ll mod)
{
ll res = 1;
x %= mod;
while (k > 0)
{
if (k & 1)
res = res * x % mod;
x = x * x % mod;
k >>= 1;
}
return res;
}
void solve()
{
ll inv = qmi(10000, MOD - 2, MOD);
int n;
cin >> n;
vi a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
vi p(n);
for (int i = 0; i < n; i++)
{
cin >> p[i];
}
vl f(1024, 0);
f[0] = 1; // 初始状态,只有 0 的概率为 1
for (int i = 0; i < n; i++)
{
vl g(1024);
for (int x = 0; x < 1024; x++)
{
// 不选当前元素的情况
g[x] = (g[x] + f[x] * (10000 - p[i])) % MOD;
// 选中当前元素的情况
g[x] = (g[x] + f[x ^ a[i]] * p[i]) % MOD;
}
for (int x = 0; x < 1024; x++)
{
g[x] = g[x] * inv % MOD;
}
f = g;
}
ll ans = 0;
for (int x = 0; x < 1024; x++)
{
ll sq = (1LL * x * x) % MOD;
ans = (ans + sq * f[x]) % MOD;
}
cout << ans << "\n";
}







没有回复内容