求最大公因数
求两数的最大公因数通常的做法是对两个数因式分解,找出共同的素数,然后求出最大公因数(GCD)。但是当数字越大时,因式分解就越困难,此时,使用欧几里得算法就能高效求出其最大公因数。
欧几里得算法
欧几里得算法(又称辗转相除法)用于计算两个数的最大公因数,被称为是世界上最古老的算法。
基本思想
两个正整数
a和b,它们的最大公约数(gcd(a,b))与b和a除以b得到的余数的最大公约数(gcd(b,a%b))相同。
通过不断用较小的数替换较大的数,并取余数,最终在余数为0时找到最大公约数。
举例说明
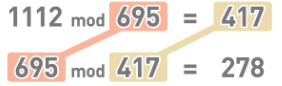
以求1112与695这两个数的最大公约数为例:
-
首先用较大的数字除以较小的数字,求出余数,也就是堆两个数字进行模运算。得到余数
417

-
接下来再用除数
695和余数417进行模运算,结果为278。
-
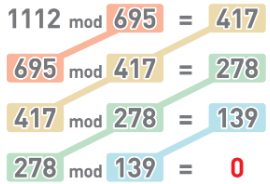
继续进行同样的操作,对
417和278作模运算,结果为139。

-
对
278和139作模运算,结果为0,也就是说278可以被139整除。
-
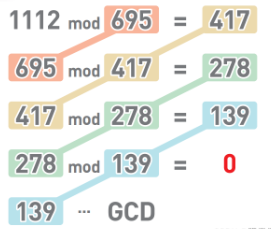
余数为0时,最后一次运算中的除数
139就是1112和695的最大公约数。
算法实现
#include "iostream"
using namespace std;
/*欧几里得算法—求最大公约数—迭代实现*/
int gcd(int a, int b){
while (b != 0){
int tmp = a;
a = b;
b = tmp % b;
}
return a;
}
/*欧几里得算法—求最大公约数—递归实现*/
int gcd_dg(int a, int b){
return b == 0 ? a : gcd_dg(b, a % b);
}
int main(){
cout << gcd(1112, 695) << endl;
cout << gcd_dg(1112, 695) << endl;
system("pause");
return 0;
}











没有回复内容