【牛客训练记录】牛客小白月赛106

训练情况

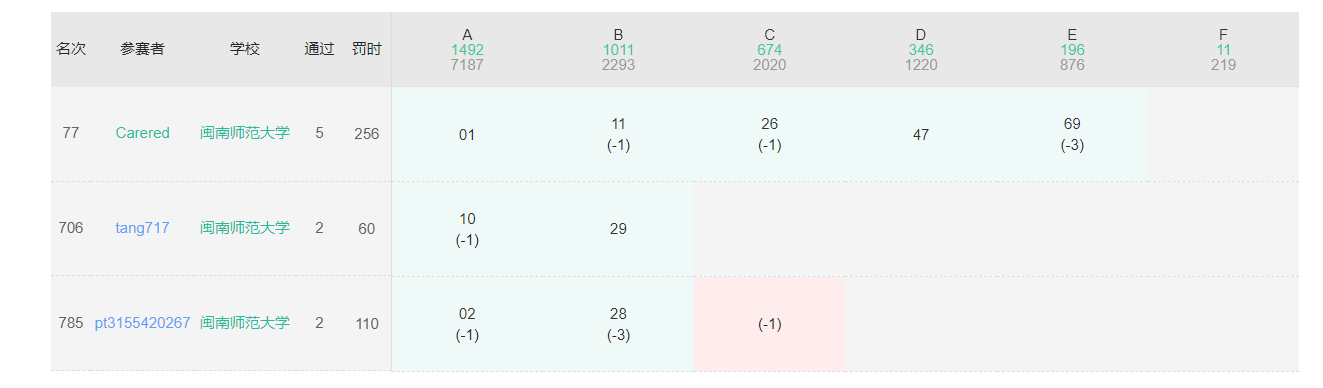
赛后反思

由于是周五晚上，C题猜了一个假结论，做到后面摆了

A题

这题只关心答案的奇偶性，我们注意到偶数的非零次方是偶数，奇数的非零次方是奇数，所以我们就不需要求幂，但是注意一下偶数的 \(0\) 次方会改变奇偶性。

#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

void solve(){
    int a,b,c,d; cin>>a>>b>>c>>d;
    if(b == 0) a = 1;
    if((a*c+d)&1) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

B题

交集刚好为 \(1\)，并且每个数只能最多出现两次，我们考虑构造下面的一种情况，依次类推，第一行与第二、三、四行都恰有一个交集，第二行与第三、四、五行都恰有一个交集。

1 2 3 4 5 6 7
2 8 9 10 11 12
3 9
4 10
5 11
6 12
7 13

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

const int N = 607;

int n;
int a[N][N];

void solve(){
    cin>>n;    
    int tot = 0;
    for(int i = 1;i<=n;i++){
        for(int j = i;j<=n;j++){
            ++tot;
            a[i][j] = tot;
        }
    }
    tot = 0;
    for(int i = 1;i<=n;i++){
        for(int j = i;j<=n;j++){
            ++tot;
            a[j][i] = tot;
        }
    }
    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=n;j++){
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}