质数-质数筛选、质因数分解、互质判定

质数筛选

对于一个正整数 N，一次性求出 1～N 之间所有的质数，即为质数筛选。

显然根据上述「质数判定」的内容，我们可以通过枚举 1～N 的所有数，再依次使用「试除法」来判定其是否为质数，从而完成质数的筛选。但此种方法的时间复杂度过高，为 O(N√N) 。

质数筛选经典方法：「Eratosthenes 筛法」，也被称为「埃式筛」。该算法基于一个基本判断：任意质数 x 的倍数 ( 2x,3x,… ) 均不是质数。

算法流程：

• 将 2～N中所有数标记为 0
• 从质数 2 开始从小到大遍历 2～N 中所有自然数
• 如果遍历到一个标记为 0 的数 x ,则将 ≤ N 中 的 x 的所有倍数标记为 1

如果一个数 x 的标记为​ 0，则代表这个数不是 2～(x−1) 中任何数的倍数，即 x 为质数。

#include <iostream>
using namespace std; #include <vector>

int main(){ int n;cin >> n; vector<bool> visit(n+1,true);//先默认所有数都是质数
    vector<int> isPrime; for(int i = 2;i <= n;++i){ if(visit[i] == true){ isPrime.push_back(i); for(int j = i;j <= n;j += i)  visit[j] = false; } } for(int i = 0;i < isPrime.size();++i)  cout << isPrime[i] << endl; }

质因数分解

根据「唯一分解定理」，任何一个大于 1 的正整数都能唯一分解为有限个质数的乘积：

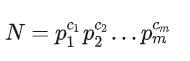
其中 ci 均为正整数，而 pi 均为质数，且满足 p1<p2<…<pm 。

根据上述定理，只需要求出所有的 pi,ci ，即可完成对 N 的质因数分解。

首先考虑如何求 p1 和 c1 。

由于 p1<p2<…<pm ，且 p1 为质数，因此不难发现， p1 是 N 所有因子中除 1 以外最小的数。

因此我们可以枚举 2～N 中的所有数 x，如果 N 是 x 的倍数，则 x 为 p1。得到 p1 后，我们可以令 N 不断除以 p1 直至其不再为 p1 的倍数，则 c1 等于除以 p1 的总次数。

得到 p1 和 c1 后，N 去除了所有的 p1，因此 N 变为 p2c2…pmcm。又由于 p1<p2 ，因此我们继续枚举 x，如果再次出现 N 是 x 倍数的情况，则 x 为 p2 。

不断使用上述算法，直至循环结束。最后还需判断 N 是否为 1，如果 N 不为 1，则 pm=N,cm=1 。

该算法的时间复杂度为 O(N)

#include <iostream>
using namespace std; #include <vector>

int main(){ int n;cin >> n; vector<int> p,c; for(int i = 2;i*i <= n;++i){ if(n % i == 0){ p.push_back(i); int count = 0; while(n % i == 0){ ++count;n /= i; } c.push_back(count); } } if(n > 1){//最后的质数
        p.push_back(n);c.push_back(1); } for(int i = 0;i < p.size();++i)  cout << p[i] << " " << c[i] << endl; }

互质判定

如何判断两个自然数互质。

「最大公约数」：如果自然数 c 同时是自然数 a 和 b 的约数，即 a 和 b 同时是 c 的倍数，则 c 为 a 和 b 的公约数。

「最大公约数」就是 a 和 b 的所有公约数中最大的那一个，通常记为 gcd(a,b) 。

「互质」判定条件：如果自然数 a，b 互质，则 gcd(a,b)=1 。

如何求 gcd(a,b) ？此处引入「欧几里得算法」

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

两个数的乘积除以它们的最大公约数的商就是它们的最小公倍数。