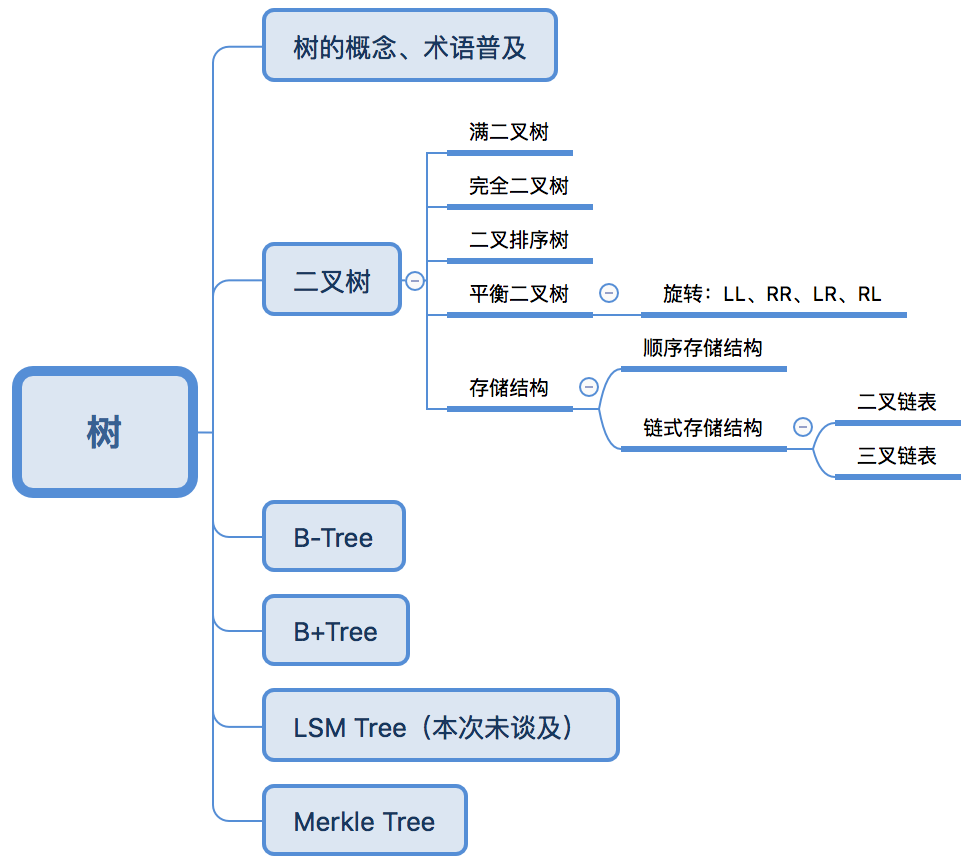
概念

• 父结点：当一个结点有子节点，该结点称为其的父结点

• 子节点：一个结点含有的子树的根结点称为该结点的子结点

• 兄弟结点：拥有相同父结点的结点互称为兄弟结点

• 结点的度：一个结点拥有的子树的个数称为该结点的度

• 树的度：一棵树中，最大的结点度称为树的度

• 结点层次：从根开始算，根为第一层，根的子结点为第二层，以此类推

• 树的深度或高度：树中结点的最大层次数

• 森林：m棵互不相交的树的集合（把树的根结点删除就成了森林）

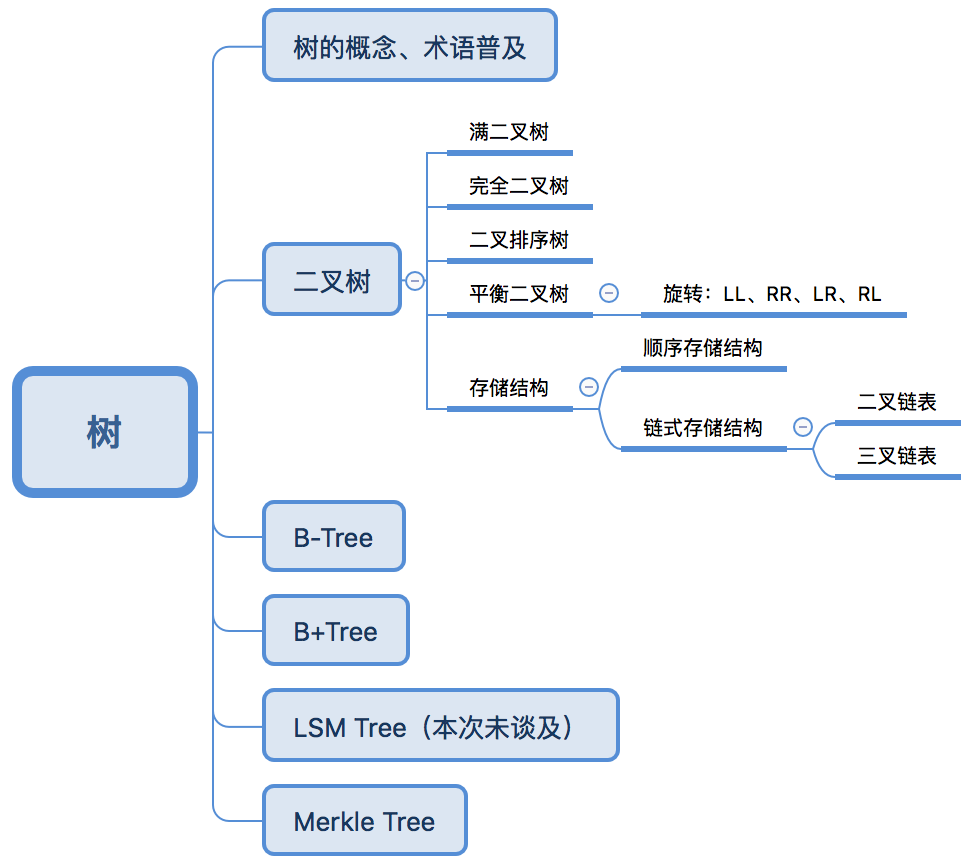
二叉树

概念

  每个结点至多有两棵子树，当结点数等于0时，为空二叉树，大于0时，有左右之分，顺序不能颠倒

特殊的二叉树

斜树

所有的结点都在左子树的二叉树称为左斜树，所有结点都在右子树的二叉树称为右斜树，它们合称为斜树

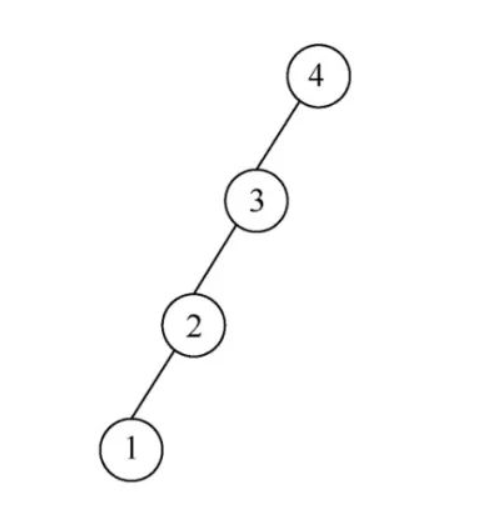
满二叉树

当二叉树的每一层的结点数都达到最大值称为满二叉树

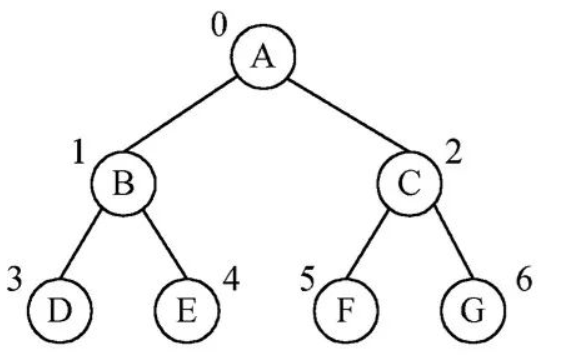
完全二叉树

除了最后一层所有层的结点数都达到最大值，最后一层的结点按照从左到右的顺序排列

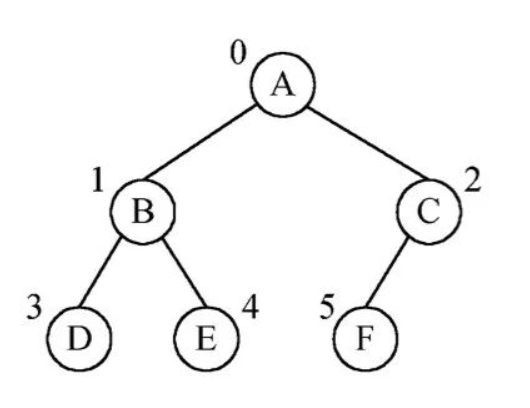
二叉排序树

左子树上的所有结点的关键字都小于根结点的关键字，右结点上的所有结点的关键字都大于根节点的关键字，左子树和右子树各是一棵二叉排序树

平衡二叉树

树上任一结点的左右子树的高度之差绝对值不超过1，它的左子树和右子树都是平衡二叉树，另外结点的平衡因子 = 左子树高度 – 右子树高度，在平衡二叉树中任何一个结点的平衡因子只能是0、1、-1

二叉树的存储结构

顺序存储结构

对于完全二叉树，结点按照从上到下、从左到右的顺序进行编号

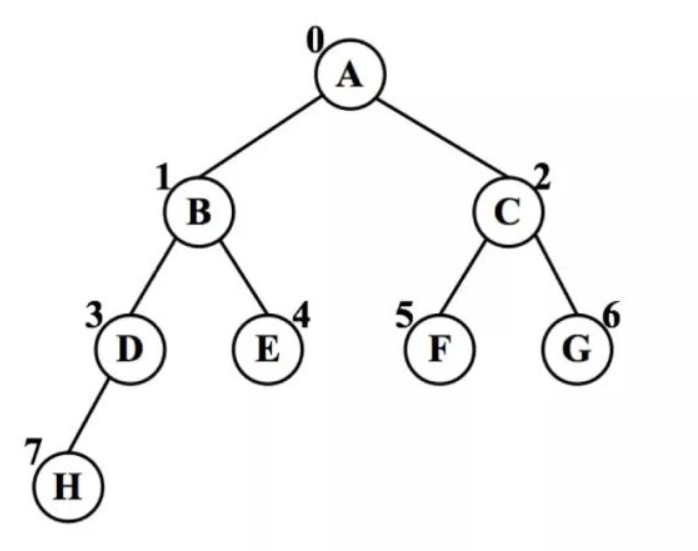
对于非完全二叉树，需要通过补充空子树的方法，将非完全二叉树变为完全二叉树，然后进行顺序存储，但是如果考虑一种极端情况，树为右斜树或者左斜树，这样存储空间会浪费很多，所以改变，采用两条链分别连接左右两个子树，就是链式存储结构

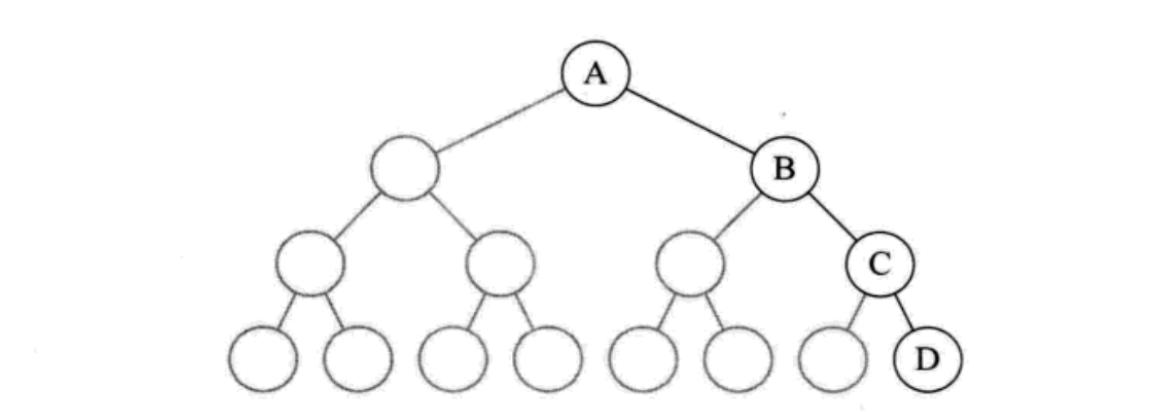
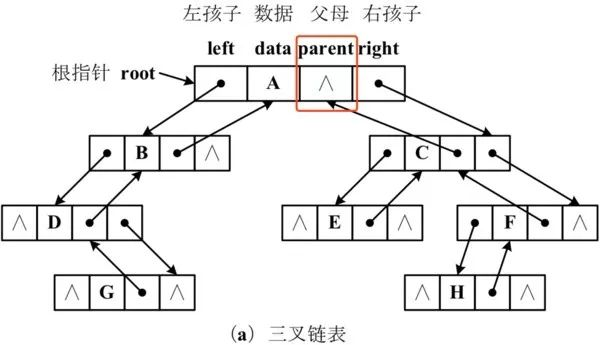
二叉链表

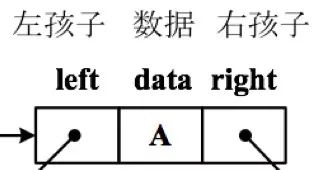
  采用两条链分别连接左、右孩子，每个结点有三个域：data 存储数据元素，left、right 分别指向左、右孩子结点，结构如下

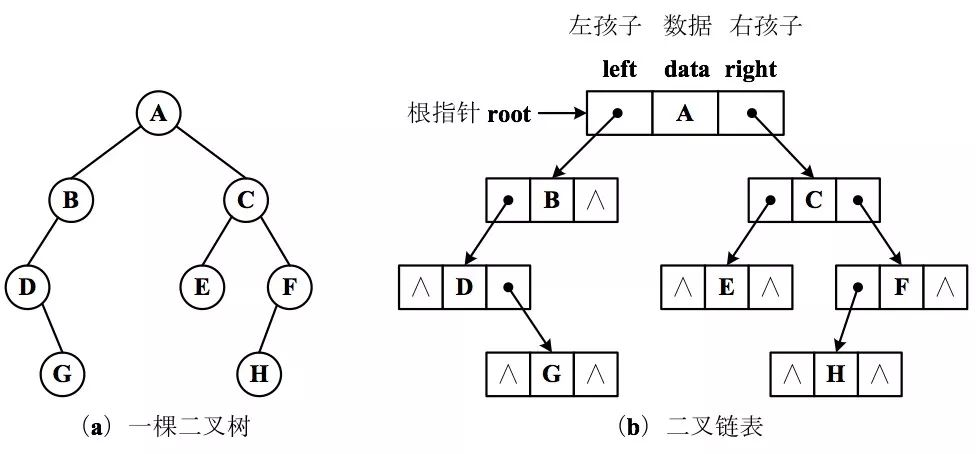
来源链接：https://www.cnblogs.com/codyxz/p/18657133