一些必要 trick

1. 推式子，先提 \(\sum\) 和 \(\Pi\) 到最前面，然后从后往前合并，必要时考虑更改 \(\sum\) 的取值
2. 看到次方变为斯特林数，\(x^n=\sum\limits_{i=0}^{n} {n \brace i}{x \choose i}i!=\sum\limits_{i=0}^{n}\sum\limits_{i=1}^m{(-1)^{m-i}\frac{i^n}{(m-i)!}}{x \choose i}\)
3. 注意莫反、欧反的形式

前置数学知识

函数

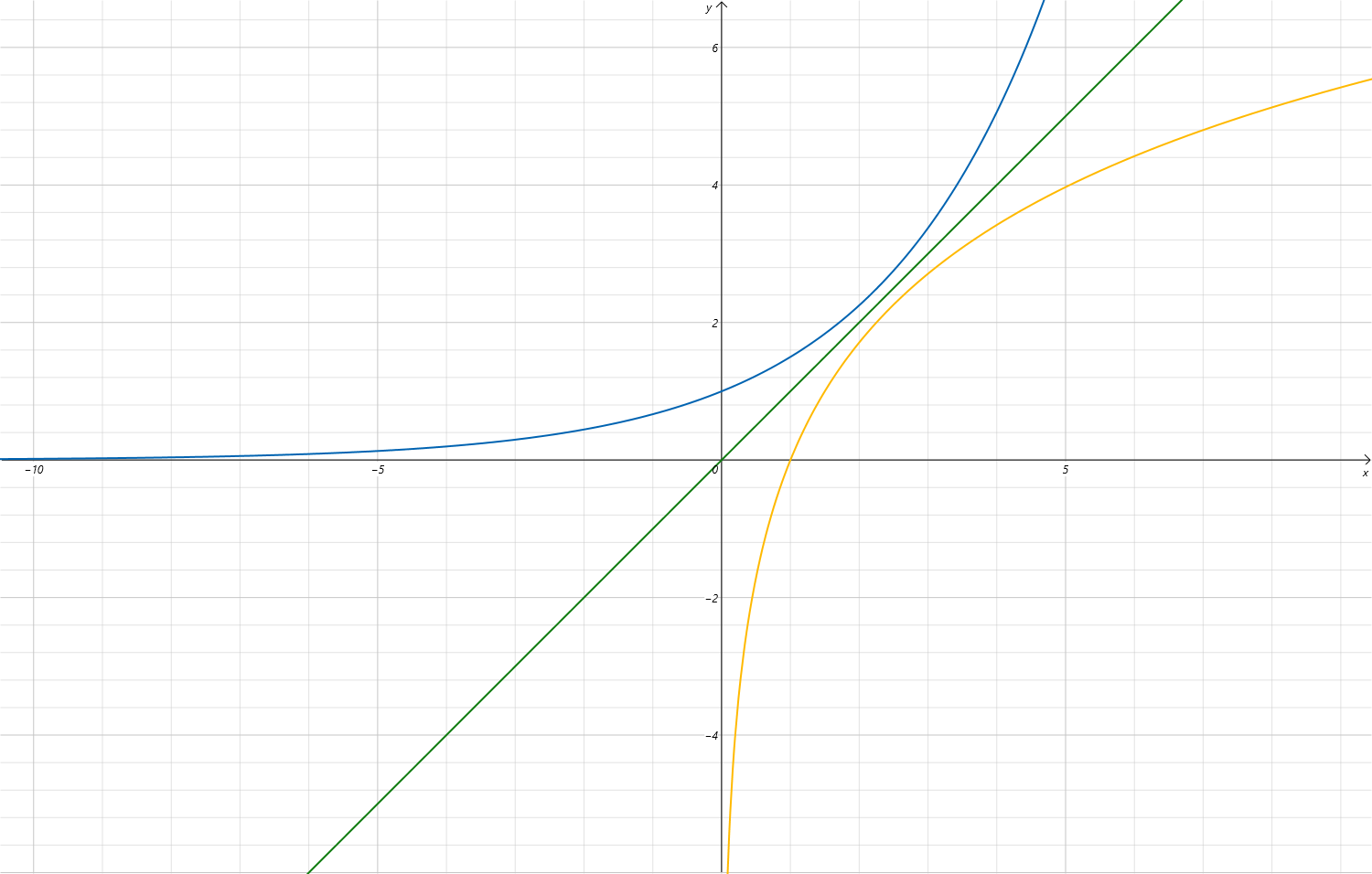
指数函数

\(y=a^x\)

对数函数

\(y=\log_ax\)

\(x^{\frac{a}{b}}=\sqrt[b]{x^a}\)

\(\log_ax+\log_ay=\log_axy\)

对指数函数关于直线 \(y=x\) 对称

离散数学

集合

\({}\mathbb{S}=\left \{1,2,3,5 \right \}\)

\(x=3,x\in\mathbb{S}\)

\(y=4,y\notin\mathbb{S}\)

\(\mathbb{S’}=\left\{1,2,3 \right\},\mathbb{S’}\subseteq\mathbb{S}\)

\(\mathbb{S”}=\left\{1,2,4 \right\},\mathbb{S”}\subsetneq\mathbb{S}\)

空集$ \phi $为任何非空集的子集。

映射

• 两个集合中每一个元素都有相对应的元素，称为满射。
• 两个集合中其中两个元素仅与另一个元素对应，称为单射。
• 两个集合中所有元素一一对应，称为一一映射（双射）。
• 两个集合等势，即可形成一一映射（双射）。
  例：${ x|1\le x\le2} $ 与 $ { y|2\le y\le 5} $ 等势。

数列

\[{a=\{2,3,4,4,2\}} \]

\[\text{则 }{a_1=2,a_2=3,a_3=3,a_4=4,a_5=2} \]

• 等差数列：

\[{a_n=a_1+(n-1)d} \]

\[{\sum_{i=1}^{n}a_i=\frac{(a_1+a_n)n}{2}} \]

• 等比数列：

\[{a_n=a_1\cdot q^{n-1}} \]

\[{\sum_{i=1}^{n}a_i=\frac{a_1(1-q^n)}{1-q}} \]

数论

最大公约数

\[{\gcd(a,b)=\gcd(b,a\mod b)} \]

最小公倍数

\[{\operatorname{lcm}(a,b)=\frac{xy}{\gcd(x,y)}} \]

\[{\operatorname{lcm}(x,y)\cdot\gcd(x,y)=xy} \]

裴蜀定理

• 内容：设 \(a,b\) 是不全为零的整数，对任意整数 \(x,y\)，满足 \(\gcd(a,b)\mid ax+by\)，且存在整数 \(x,y\), 使得 \(ax+by=\gcd(a,b)\).
• 逆定理：设 \(a,b\) 是不全为零的整数，如果 \(d>0\) 是 \(a,b\) 的公因数，且存在整数 \(x,y\)，使得 \(ax+by=d\)，那么 \(d\) 就是最大公因数 \(\gcd(a,b)\)
• 推广：设\(a_1,a_2,…,a_n\) 是不全为零的整数，一定存在整数 \(x_1,x_2,…,x_n\)，使得 \(a_1x_1+a_1x_2+…+a_nx_n=\gcd(a_1,a_2,…,a_n)\)
• 推论：方程 \(ax+by=n\)，\(n>ab-a-b\) 时总有解，\(n=ab-a-b\) 是最大无解情况
• 裴蜀定理进一步结论：
  若 \(\gcd(a,b)=1\)，对于方程 \(ax+by=n\)，设\(C=ab-a-b\)，则 \(n,C-n\) 中有且仅有一个有非负数解，且有如下关系：

\(n\) 的值域	有非负数解
\((-\infty,0)\)	\(0\)
\(0\)	\(1\)
\((0,C)\)	\(-\)
\(C\)	\(0\)
\((C,\infty)\)	\(1\)

欧几里得引理（Euclid’s lemma）

• 内容
  \(c|ab,\gcd(a,c)=1\Rightarrow c|b\).

\(p|ab\Rightarrow p|a\text{或}p|b\).

证明

由裴蜀定理得 \(au+cv=1\).

\(\Rightarrow aub+cvb=b\).

\(\Rightarrow c\mid b\).

拓展欧几里得

根据以下两个定理，可以求出线性同余方程 \(ax\equiv b \pmod n\) 的解。

定理 1：线性同余方程 \(ax\equiv b \pmod n\) 可以改写为如下线性不定方程：

\[ax + nk = b \]

其中 x 和 k 是未知数。这两个方程是等价的，有整数解的充要条件为 \(\gcd(a,n) | b\)。

应用扩展欧几里德算法可以求解该线性不定方程。根据定理 1，对于线性不定方程 \(ax+nk=b\)，可以先用扩展欧几里得算法求出一组 \(x_0,k_0\)，也就是 \(ax_0+nk_0=\gcd(a,n)\)，然后两边同时除以 \(\gcd(a,n)\)，再乘 \(b\)。就得到了方程

\[a\dfrac{b}{\gcd(a,n)}x_0+n\dfrac{b}{\gcd(a,n)}k_0=b \]

于是找到方程的一个解。

定理 2：若 \(\gcd(a,n)=1\)，且 \(x_0、k_0\) 为方程 \(ax+nk=b\) 的一组解，则该方程的任意解可表示为：

\[x=x_0+nt \]

\[k=k_0-at \]

并且对任意整数 \(t\) 都成立。

根据定理 2，可以从已求出的一个解，求出方程的所有解。实际问题中，往往要求出一个最小整数解，也就是一个特解

\[x=(x \bmod t+t) \bmod t \]

其中有

\[t=\dfrac{n}{\gcd(a,n)} \]

如果仔细考虑，用扩展欧几里得算法求解与用逆元求解，两种方法是等价的。

---

这里的 \(q\) 不需要为素数

求解 \(\gcd(a,b)\) 及满足 \(ax+by=\gcd(a,b)\) 的整数解.

第 \(i\) 步带余除法得的商为 \(q_i\)，余数为 \(r_i\).

扩展欧几里得算法可以写成：

\[r_0=a,r_1=b. \]

\[s_0=1,s_1=0. \]

\[t_0=0,t_1=1. \]

\[\vdots \]

\[r_{i+1}=r_{i-1}-r_iq_i. \]

\[s_{i+1}=s_{i-1}-s_iq_i. \]

\[t_{i+1}=t_{i-1}-t_iq_i. \]

\[\vdots \]

\[x=s_n,y=t_n,(r_{i+1}=r_iq_i). \]

唯一分解定理

• 内容
  任意一个正整数 \(a\ge2\)，必然有且仅有一种形如 \(p^{\alpha_1}_1p^{\alpha_2}_2p^{\alpha_3}_3\cdots p^{\alpha_k}_k\) 的分解方法，其中，\(p_i<p_{i+1}\)，\(\alpha_i\) 为正整数，\(0<i\le k\).

证明

设 \(m\) 为最小的不满足此定理的 \(a\)，\(m\) 的两种表示方法为：

\[p^{\alpha_1}_1p^{\alpha_2}_2p^{\alpha_3}_3\cdots p^{\alpha_k}_k \]

\[q^{\beta_1}_1q^{\beta_2}_2q^{\beta_3}_3\cdots q^{\beta_g}_g \]

则 \(p_1\mid q^{\beta_1}_1q^{\beta_2}_2q^{\beta_3}_3\cdots q^{\beta_g}_g\)，由欧几里得引理知 \(p_1\mid q_j\) (不妨把这个 \(q_j\) 设为 \(q_1\) )，由于 \(q_1\) 是个质数，所以 \(p_1=q_1\)，那么设数 \(n=\frac{m}{p_1}=\frac{m}{q_1}\)，很明显 \(n<m\)，又发现 \(n\) 可以表示为：

\[p^{\alpha_1-1}_1p^{\alpha_2}_2p^{\alpha_3}_3\cdots p^{\alpha_k}_k \]

\[q^{\beta_1-1}_1q^{\beta_2}_2q^{\beta_3}_3\cdots q^{\beta_g}_g \]

所以 \(m\) 不是最小的不满足此定理的 \(a\).

欧拉筛

欧拉函数

• 定义

\[\varphi(a)=\sum^n_{i=1}[\gcd(i,n)=1] \]

• 计算公式

\[\varphi(a)\varphi(b)=\varphi(ab),\gcd(a,b)=1. \]

\[\varphi(p)=p-1. \]

\[\varphi(p^k)=p^k-p^{k+1}. \]

同余类

模 \(n\) 同余的数构成 \(n\) 的一个同余类.又称“剩余类”，同余类中的每个元素都可以拿来代表该同余类，称为该同余类的代表数.

剩余系

从构成 \(n\) 的不同同余类中取各一个数组成的集合，它们互不同余.

完全剩余系，最小剩余系和简约剩余系

完全剩余系是从构成 \(n\) 的每个同余类中取各一个数组成的集合.（\(n\) 个元素）

如果里面的每个元素都是该同余类中最小的非负整数，称它为最小剩余系.（\(n\) 个元素）

将完全剩余系中去掉与模 \(n\) 不互素的元素，得到简约剩余系.（\(\varphi(n)\) 个元素）

完全剩余系的性质

• 内容
  若 \(A\) 是 \(n\) 的一个完全剩余系，且 \(\gcd(a,b)=1\)，则 \(aA+b\) 也是 \(n\) 的一个完全剩余系.

同余

\[{a\equiv b\pmod p} \normalsize\texttt{，则} {a=b+kp(k\in \mathbb{Z})} \]

费马小定理

\[a^{p-1}\equiv1\pmod p. \]

\[a^p\equiv a\pmod p. \]

其中第一行需要 \(\gcd(a,p)=1\).

欧拉函数

欧拉函数(Euler’s totient function)，即 \(\varphi(n)\)，表示的是小于等于 \(n\) 的数中与 \(n\) 互质的数字个数，

例如 \(\varphi(1)=1\)。

性质

\(\bullet 1.\) 欧拉函数是积性函数。

$\ \ $ 积性函数的意思是：如果有 \(\gcd(a,b)=1\)，那么则有 \(\varphi(a)=\varphi(a) \times \varphi(b)\)。

$\ \ $ 特别的，当 \(n\) 为奇数时，\(\varphi(2n)=\varphi(n)\)。

\(\bullet 2.\) 当 \(n\) 为质数时，有 \(\varphi(n)=n-1\)。

\(\bullet 3.\) \(\forall n>1,1\)~\(N\) 中所有与 \(n\) 互质的数的和为 \(\frac{n\cdot \varphi(n)}{2}\)

\(\hspace{0.5em}\)

证明

\(\hspace{0.5em}\) 根据更相相减法，因为 \(\gcd(n,x)=\gcd(n,n-x)\)，所以予 \(n\) 互质的数 \(x,n-x\) 成对出现，平均值为 \(\frac{n}{2}\)，故和为 \(\frac{n\cdot \varphi(n)}{2}\)

\(\bullet 4.\) 若 \(p\) 为质数，则 \(\varphi(p^k)=p^k-p^{k-1}\)。

\(\hspace{0.5em}\)

证明

\(\hspace{0.5em}\) 因为 \(p\) 为质数，所以与 \(p\) 不互质的数就只能为 \(p\) 的倍数，共 \(p^{k-1}\) 个。所以减去这些就是 \(\varphi(n)\) 的值。

\(\bullet 5.\) 若 \(p\) 为质数，若 \(p\mathrel{|}n\) 且 \(p^2\mathrel{|}n\)，则 \(\varphi(n)=\varphi(\frac{n}{p})\cdot p\)；若\(p\)为质数，若 \(p\mathrel{|}n\) 且 \(p^2\nmid n\)，则 \(\varphi(n)=\varphi(\frac{n}{p})\cdot(p-1)\)

\(\hspace{0.5em}\)

证明

\(\hspace{0.5em}\) 第一条：因为 \(n\) 与 \(\frac{n}{p}\) 的质因子相同，只是 \(p\) 的指数不同。所以 \(\frac{\varphi(n)}{\varphi(\frac{n}{p})}=p\)，即可得原式。

\(\hspace{0.5em}\) 第二条：根据性质一，即欧拉函数为积性函数，可得 \(\varphi(n)=\varphi(\frac{n}{p})\cdot\varphi(p)\)，因为 \(p\) 为质数，由性质二可得原式。

\(\bullet 6.\) \(n=\sum\limits_{d\mathrel{|}n}^{}\varphi(d)\)。

\(\hspace{0.5em}\) 证明如下图：

用法

举个栗子:The Euler function

题意：求\(\sum\limits_{i=a}^{b}\varphi(i)\)

如果枚举必定 \(TLE\)。

方法一：

用埃氏筛，由欧拉函数的展开式 \(\varphi(N)=N\cdot\prod\limits_{质数p\mid N}^{}(\frac{p-1}{p})\)，

对于筛出的每个质数 \(p\)，将 \(p\) 的倍数的欧拉函数值除以 \(p\) 再乘 \(p-1\) 即可。

时间复杂度 \(O(N\log N)\)。

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
template<typename P>
inline void read(P &x){
   	P res=0,f=1;
   	char ch=getchar();
   	while(ch<'0' || ch>'9'){
   		if(ch=='-') f=-1;
   		ch=getchar();
   	}
   	while(ch>='0' && ch<='9'){
   		res=res*10+ch-'0';
   		ch=getchar();
	}
	x=res*f;
}
using namespace std;
const int N=3000005;
int a[N],b[N],tot=1,maxn;
int phi[N];
void initprime(int n){
	for(int i=2;i<=n;i++) phi[i]=(int)i;
	for(int i=2;i<=n;i++) if(phi[i]==(int)i)
		for(int j=i;j<=n;j+=i) phi[j]/=(int)i,phi[j]*=(int)(i-1);
	for(int i=1;i<=n;i++) phi[i]+=phi[i-1];
}
signed main(){
	auto solve=[&](){
		while(scanf("%d%d",&a[tot],&b[tot])!=EOF) maxn=max(maxn,b[tot]),tot++;
		initprime(maxn);
		for(int i=1;i<tot;i++) printf("%lld\n",phi[b[i]]-phi[a[i]-1]);
		return;
	};
	return 0;
}

方法二自己搜，不想写了。

欧拉定理

当 \(\gcd(a,n)=1\) 时：

\[a^{\varphi(n)}\equiv1\pmod n. \\ \]

乘法逆元

如果一个线性同余方程 \(ax \equiv 1 \pmod b\)，则 \(x\) 称为 \(a \bmod b\) 的逆元，记作 \(a^{-1}\)。

• 扩展欧几里得法

void exgcd(int a, int b, int& x, int& y) {
  if (b == 0) {
    x = 1, y = 0;
    return;
  }
  exgcd(b, a % b, y, x);
  y -= a / b * x;
}

扩展欧几里得法和求解线性同余方程是一个原理，在这里不展开解释。

• 快速幂法

因为 \(ax \equiv 1 \pmod b\)；

所以 \(ax \equiv a^{b-1} \pmod b\)（根据 费马小定理）；

所以 \(x \equiv a^{b-2} \pmod b\)。

int qpow(long long a, int b) {
  int ans = 1;
  a = (a % p + p) % p;
  for (; b; b >>= 1) {
    if (b & 1) ans = (a * ans) % p;
    a = (a * a) % p;
  }
  return ans;
}

注意：快速幂法使用了 费马小定理，要求 \(b\) 是一个素数；而扩展欧几里得法只要求 \(\gcd(a, b) = 1\)。

约数数量

\[{(k_1+1)\times(k_2+1)\times…\times(k_n+1)} \]

\[{\sum_{i=1}^{n}{k_i+1}} \]

约数和

\[{\prod_{i=1}^{n}}{\sum_{j=1}^{}{{p}^{k_j}_{i}}} \]

容斥原理

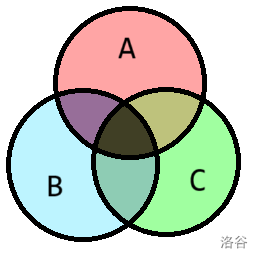
\[{A\cup B\cup C=A+B+C-A\cap B-A\cap C-B\cap C+A\cap B\cap C} \]

排列组合

• 定义:
  从 \(n\) 个数中选 \(m\) 个数考虑顺序组合方法数:

\[{A}_{ n}^{ m}{=\frac{n!}{(n-m)!}} \]

• 定义:
  从 \(n\) 个数中选 \(m\) 个数不考虑顺序组合方法数:

\[{C}_{n}^{m}{=\frac{n!}{m!(n-m)!}} \]

\[{C}_{{n+1}}^{k}={C}_{{n}}^{k}+{C}_{{n}}^{k-1} \]

卡特兰数

该递推关系的解为：

\[H_n = \frac{\binom{2n}{n}}{n+1}(n \geq 2, n \in \mathbf{N_{+}}) \]

关于 Catalan 数的常见公式：

\[H_n = \begin{cases} \sum_{i=1}^{n} H_{i-1} H_{n-i} & n \geq 2, n \in \mathbf{N_{+}}\\ 1 & n = 0, 1 \end{cases} \\ H_n = \frac{H_{n-1} (4n-2)}{n+1} \\ H_n = \binom{2n}{n} – \binom{2n}{n-1} \]

二项式定理

在进入排列组合进阶篇之前，我们先介绍一个与组合数密切相关的定理——二项式定理。

二项式定理阐明了一个展开式的系数：

\[(a+b)^n=\sum_{i=0}^n\binom{n}{i}a^{n-i}b^i \]

证明可以采用数学归纳法，利用
\(\dbinom{n}{k}+\dbinom{n}{k-1}=\dbinom{n+1}{k}\) 做归纳。

二项式定理也可以很容易扩展为多项式的形式：

设 \(n\) 为正整数，\(x_i\) 为实数，

满足的非负整数解

\[(x_1 + x_2 + \cdots + x_t)^n = \sum_{满足 n_1 + \cdots + n_t=n 的非负整数解} \binom{n}{n_1,n_2,\cdots,n_t} x_1^{n_1}x_2^{n_2}\cdots x_t^{n_t} \]

其中的
\(\dbinom{n}{n_1,n_2,\cdots,n_t}\) 是多项式系数，它的性质也很相似：

\[\sum{\binom{n}{n_1,n_2,\cdots,n_t}} = t^n \]

第二类斯特林数

• 定义:
  将n个不同的元素拆分成m个集合的方案数，记为:

\[{S(n,m)} \]

• 性质:

\[{S(n,0)=0} \]

\[{S(n,1)=1} \]

\[{S(n,n)=1} \]

\[{S(n+1,m)=S(n,m-1)+m\cdot S(n,m)} \]

复数

• $\text{形如 }i=\sqrt{-1} $

\(\text{便能有 }i^2=-1\)

\(\text{在复实数坐标轴上，一个点表示为 }A=a+bi，\text{同等转化到笛卡尔坐标系，相当于 }A(a,bi)\)

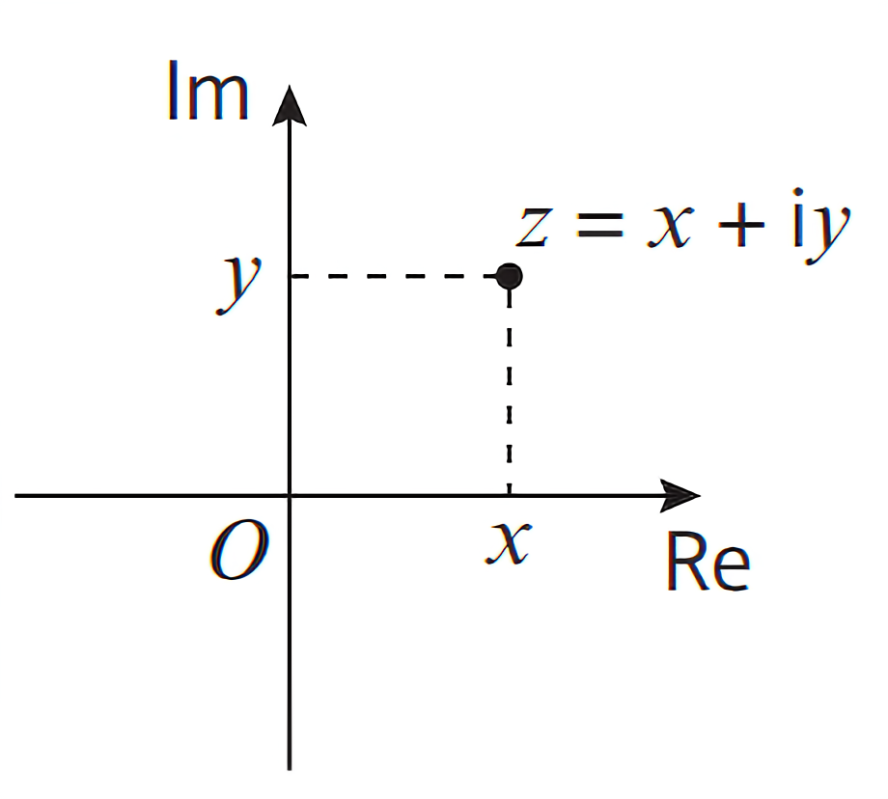
• $\text{复数运算定义为:} $

\[A=a+bi \\ B=c+di \\ 则 A+B=a+c+bi+di \\ 也有 A\cdot B 表示为 A 的幅度加 B 的幅度，其长度为 A\cdot B \]

概率与期望

概率

• 概率一般用 \(P\) 表示
• 性质:

1.单调性：\(若A\subset B，则有 P(A)\le P(B)\)

2.容斥原理：\(P(A+B)=P(A)+P(B)-P(AB)\)

3.\(P(A+B)=P(A)-P(AB)，这里A-B表示差集\)

• \(P(B|A)=\frac{P(B|A)P(B)}{P(A)}\)

期望

• 期望一般用 \(E\) 表示
• 性质：

1.线性性：若随机变量 \(X,Y\) 的期望存在，则

对任意实数 \(a,b\)，有 \(E(aX+b)=a\cdot EX+b\)

\(E(X+Y)=E(X)+E(Y)\)

2.随机变量乘积的期望

若随机变量 \(X,Y\) 的期望存在且 \(X,Y\) 相互独立，则有

\(E(XY)=EX\cdot EY\)

注意：上述性质中的独立性 并非 必要条件。

期望与概率的转化

对于随机事件 \(A\)，考虑其示性函数 \(I_A\)：

\[I_A(\omega) = \begin{cases} 1, & \omega \in A \\ 0, & \omega \notin A \end{cases} \]

根据定义可以求得其期望 \(EI_A = P(A)\)。这一转化在实际应用中非常常见。

方差

定义

设随机变量 \(X\) 的期望 \(EX\) 存在且期望

\[E(X – EX)^2 \]

也存在，则称上式的值为随机变量 \(X\) 的 方差，记作 \(DX\) 或 \(Var(x)\)。方差的算术平方根称为标准差，记作 \(\sigma(X) = \sqrt{DX}\)。

方差的性质

若随机变量 \(X\) 的方差存在，则

对任意常数 \(a, b\) 都有 \(D(aX + b) = a^2 \cdot DX\)

\(DX = E(X^2) – (EX)^2\)

协方差与相关系数

一般来说，等式 \(D(X + Y) = DX + DY\) 并不成立，我们自然会提出两个问题：

\(D(X + Y)\) 与 \(DX + DY\) 之间相差的部分到底是什么。
\(D(X + Y)\) 与 \(DX + DY\) 在什么情况下相等。
对于第一个问题，我们引入协方差作为解答。

协方差的定义

对于随机变量 \(X, Y\)，称

\[E((X – EX)(Y – EY)) \]

为 \(X\) 与 \(Y\) 的 协方差，记作 \(\operatorname{Cov}(X, Y)\)。

协方差的性质

对于随机变量 \(X, Y, Z\)，有

\(\operatorname{Cov}(X, Y) = \operatorname{Cov}(Y, X)\)

对任意常数 \(a, b\)，有 \(\operatorname{Cov}(aX + bY, Z) = a \cdot \operatorname{Cov}(X, Z) + b \cdot \operatorname{Cov}(Y, Z)\)

同时协方差与方差也有如下联系：

\(DX = \operatorname{Cov}(X, X)\)

对于刚才提出的第二个问题，不难看出 \(D(X + Y) = DX + DY\) 当且仅当 \(\operatorname{Cov}(X, Y) = 0\)。一个直观的必要条件是 \(X\) 与 \(Y\) 独立，因为此时有

\[\operatorname{Cov}(X, Y) = E((X – EX)(Y – EY)) = E(X – EX) E(Y – EY) = 0 \]

但这个条件并不是充分的。为了描述满足 \(\operatorname{Cov}(X, Y) = 0\) 的随机变量 \(X,Y\) 之间的关系，我们引入相关系数

平面向量

• 意义：

表示为一条有长度的线段，通常表示移动一段距离，通常形式为 $ \boldsymbol{a}= \overrightarrow{AB} $

• $|AB| $ 表示为向量 $\boldsymbol{a} $ 的距离（或长度）

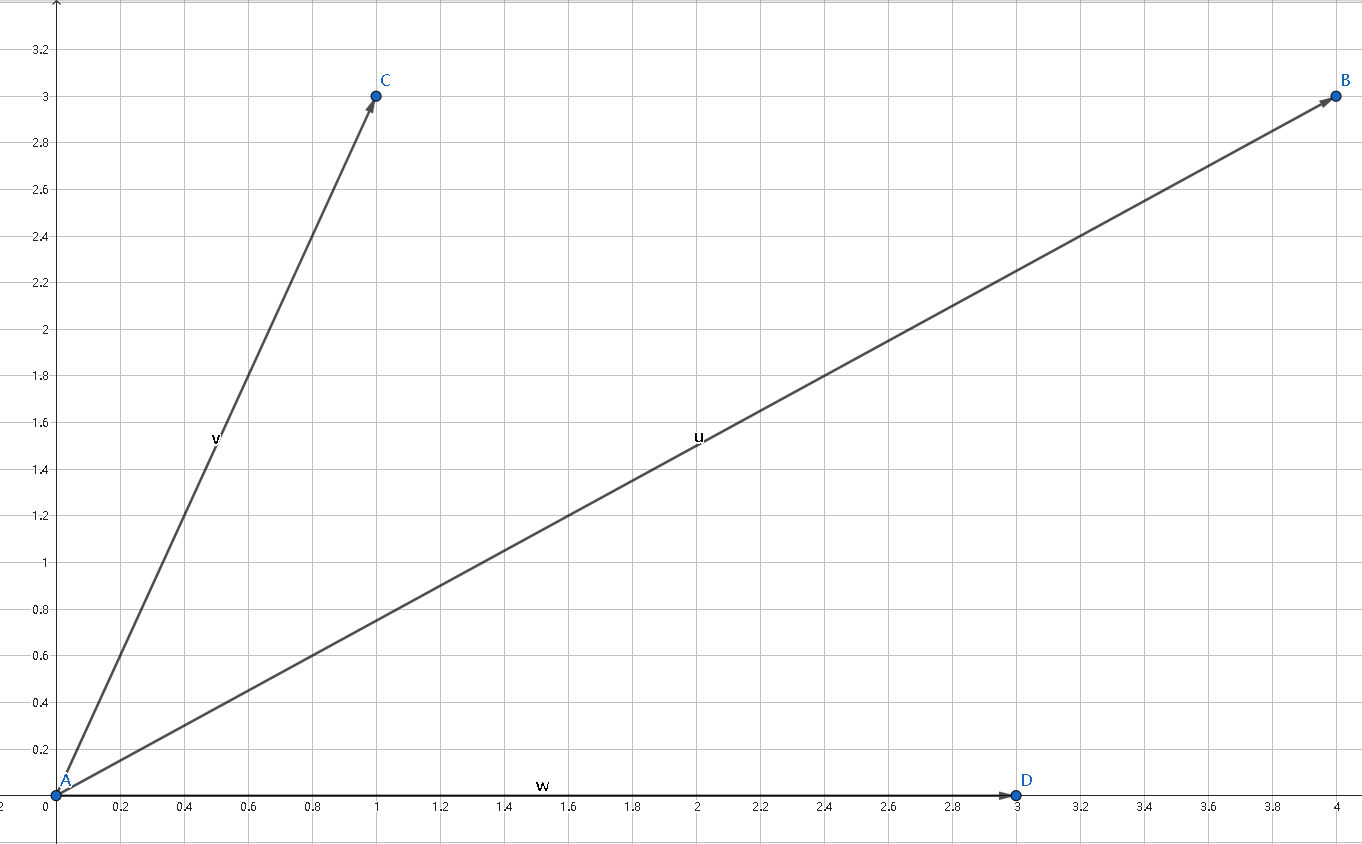
如上图中，能得出向量加减定则

\[\overrightarrow{AC}+\overrightarrow{AD}=\overrightarrow{AB} \\ \overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{AC} \\ \overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{AD} \\ \]

• 乘法定则

\[\overrightarrow{E_1}\cdot\overrightarrow{E_2}=|\overrightarrow{E_1}|\cdot|\overrightarrow{E_2}|\cdot\cos<E_1,E_2> \]

运用：例，求 \(BD\)

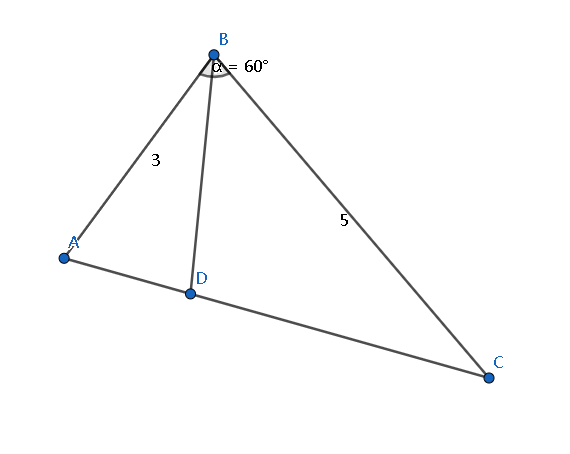
\[\begin{aligned} \overrightarrow{BD}&=\overrightarrow{BA}+\overrightarrow{AD}\\ &=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC} \\ &=\overrightarrow{BA}+\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{BC})\\ &=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC} \\ \overrightarrow{BD}\cdot \overrightarrow{BD}&=(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})^2 \\ &=\frac{4}{9}\overrightarrow{AB}^2+\frac{4}{9}\overrightarrow{AB}\cdot\overrightarrow{AC}+\frac{1}{9}\overrightarrow{AC}^2 \\ 根据向量乘法 \\ &=4+\frac{10}{3}+\frac{25}{9} \\ &=\frac{91}{9}\hspace{0.8cm} \\ \therefore \overrightarrow{BD}\cdot\overrightarrow{BD}&=|BD|^2=\frac{91}{9} \\ \therefore BD&=\frac{\sqrt{91}}{3} \end{aligned} \]

数学万恶之源

来源链接：https://www.cnblogs.com/lizihan00787/p/18685873