写在前面
- 只记录模拟赛 Div1 的题。专题授课的题实在是太多了。
- 能找到原题的都标了。
- 如你所见,作者实力有限,所以很多 T3 都没有写(所以神犇们可以不用看了)。以后可能会考虑补。
- 有问题的可以写在评论区或者私信。
Day1 模拟赛
A.最小生成树
原题:Spanning Tree Game。
Tip:注意原题与这题的数据范围的差别。
题意
给一张 \(n\) 个点,\(m\) 条边的无向图,每条边有两个可能的权值 \(a_i,b_i\),你需要对所有 \(k\in [0,m]\) 求出,当恰好有 \(k\) 条边的权值是 \(a_i\),\(m-k\) 条边的权值是 \(b_i\) 时,该图的最小生成树的边权和的最大值是多少。
数据范围:\(n\le 9,n-1\le m\le 100,a_i,b_i\le 10^8\),保证图连通且无自环,不保证没有重边。
题解
考虑 Kruskal 的流程。
将每条边拆成两条边 \((x,y,a)\) 和 \((x,y,b)\),我们称他们互为对应边。
然后把这 \(2m\) 条边按照边权升序排序。
依次考虑每条边 \((x,y,w)\)。
- 他的对应边还没有出现过,那么这条边选不选都可以(不选的话就代表这条边选了另一个边权),选的话如果此时 \(x,y\) 不连通就把 MST 的边权和加上 \(w\)。
- 他的对应边出现过了,那么如果 \(x,y\) 不连通这条边就一定要选,并把 MST 的边权和加上 \(w\),否则这条边选不选都不影响 MST。
所以设 \(f_{i,j,S}\) 表示考虑了前 \(i\) 条边,图的连通性的状态是 \(S\),有 \(j\) 条边边权选了 \(a\)。
转移的决策就是在第一种情况中选还是不选(注意第二种情况是不会对 \(j\) 这一维产生影响的,因为贡献在第一种情况里已经算过了),所以为了维护 \(j\) 这一维还需要记录每条边的 \(w\) 原来是 \(a\) 还是 \(b\)。
我们可以哈希并查集数组来记录这个 \(S\)。
合法 \(S\) 的数量为 \(Bell(n)\le 21147\),所以复杂度是 \(O(m^2Bell(n))\),但是远远跑不满。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define LL long long
#define ULL unsigned long long
using namespace std;
const int N=15,M=105,p=13331;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,ans[M];
struct Edge{
int id,x,y,w,op;
}E[M<<1];
bool flag[M<<1];
ULL End;
unordered_map<ULL,int> f[M<<1][M];
unordered_map<ULL,vector<int> > mp;
ULL HASH(vector<int> v){
ULL Hash=0;
for(int x:v) Hash=Hash*p+x;
mp[Hash]=v;
return Hash;
}
void Init(){
sort(E+1,E+2*m+1,[&](Edge e1,Edge e2){return e1.w<e2.w;});
for(int i=1;i<=2*m;i++){
for(int j=1;j<i;j++) if(E[j].id==E[i].id) flag[i]=true;
}
vector<int> v(n+1),v2(n+1);
for(int i=1;i<=n;i++) v[i]=i,v2[i]=1;
End=HASH(v2);
f[0][0][HASH(v)]=0;
}
void chkmax(int &x,int y){x=max(x,y);}
vector<int> merge(vector<int> fa,int x,int y){
int u=fa[x],v=fa[y];
if(u>v) swap(u,v);
for(int i=1;i<=n;i++) if(fa[i]==v) fa[i]=u;
return fa;
}
void dfs(int i){
if(i==2*m){
for(int j=0;j<=m;j++) ans[j]=f[i][j][End];
return;
}
int x=E[i+1].x,y=E[i+1].y,w=E[i+1].w,op=E[i+1].op;
for(int j=0;j<=min(i,m);j++){
for(pair<ULL,int> u:f[i][j]){
vector<int> fa=mp[u.fi];
int res=u.se;
if(flag[i+1]){
if(fa[x]!=fa[y]) chkmax(f[i+1][j][HASH(merge(fa,x,y))],res+w);
else chkmax(f[i+1][j][u.fi],res);
}
else{
chkmax(f[i+1][j+1-op][u.fi],res);
if(fa[x]!=fa[y]) chkmax(f[i+1][j+op][HASH(merge(fa,x,y))],res+w);
else chkmax(f[i+1][j+op][u.fi],res);
}
}
}
dfs(i+1);
}
signed main(){
freopen("mst.in","r",stdin);
freopen("mst.out","w",stdout);
n=read(),m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),a=read(),b=read();
E[i]={i,x,y,a,1},E[i+m]={i,x,y,b,0};
}
Init();
dfs(0);
for(int i=0;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
B.操作
原题:Assign or Multiply
Tip:为了卡掉 bitset 本题在原题的基础上加强了数据,并减少了时限。
题意
给定一个质数 \(p\) 和 \(n\) 个操作,操作有两种类型:
0 x:表示将 \(w\) 修改为 \(x\)。1 x:表示将 \(w\) 修改为 \((w\times x) \bmod p\)。
其中 \(w\) 是一个初始为 \(1\) 的变量。
现在你可以任意重排这些操作,问 \([0,p-1]\) 中有多少个数无论怎么重排操作都无法得到。
多测,有 \(T\) 组数据。
数据范围:\(1\le T\le 2,1\le n \le 10^6,2\le p \le 10^6,0\le x < p\),保证 \(p\) 是质数。
乱搞
来自模拟赛一位大佬的做法,直接贴上他的原题解。
![图片[1]-NOI2025 广东省队集训题解-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/05/4231725087176220777.png)
实际上因为这个题加强了,所以乱搞比正解还快。
正解
不难发现题意就是问随便选一个覆盖操作和若干乘法操作可以得到多少数。特殊的,没有覆盖操作答案是 \(p-1\)。
首先取模的乘法没有啥性质,但是注意到 \(p\) 是个质数,所以可以求出 \(p\) 的原根 \(g\),把每个数表示成 \(g^x\) 的形式(\(0\) 特判),所以就把乘法转换成加法了。然后你就把覆盖操作中的数当作背包的初值,接着对第二种操作做01背包即可,可以用 bitset 优化到 \(O(\frac{np}{w})\),显然出题人不想让你过去。
下面记 \(M=p-1\)。
观察这个背包的转移,不难发现如果现在加入的数是 \(v\) 就是要把所有满足 \(f_i=true,f_{(i+v) \bmod M} =false\) 的 \(f_{(i+v) \bmod M}\) 设为 \(true\)。
所以实际上有效的修改只有 \(O(p)\) 次,我们如果能快速找到需要修改的位置就可以保证复杂度。
但是 \(f_i=true,f_{(i+v) \bmod M} =false\) 这个限制不太好判断,不妨弱化一下,找到所有满足 \(f_i \ne f_{(i+v)\bmod M}\) 的位置,这个可以段环成链之后用树状数组维护 \(f\) 数组的哈希值然后用二分 \(O(\log^2 p)\) 求出一个符合条件的位置。
可是这样的复杂度好像不太对,因为你会找到 \(f_i=false,f_{(i+v) \bmod M} =true\) 这样没用的位置。
但是这题的背包体积这一维是在取模意义下的,换句话说,如果你按照 \(i \to (i+v)\bmod M\) 连边,你连出的显然是若干个环,这就意味此时 \(1\to 0\) 的边的数量和 \(0\to 1\) 的边的数量是相等的,所以你找出来了多少 \(1\to 0\) 的边就也找出了多少条 \(0\to 1\) 的边,而 \(1\to 0\) 的边总共只能出现 \(O(p)\) 个,所以复杂度是对的。
放在原题 \(O(n\log^2 p)\) 是稳过的,但这题你可能会被卡常反正我被卡了,这里提供两个可行的卡常方案:
- 采用二进制分组把相同的物品缩成 \(O(\log n)\) 个。
- 当加入一个物品时,先判断一下是否有合法的位置,如果没有就直接跳过这个物品,没有必要二分。
code
#include<bits/stdc++.h>
#include<cctype>
#define ULL unsigned long long
using namespace std;
const int N=1e6+5,Base=100591,MB=1<<20;
struct FastIO{
char ib[MB+100],*p,*q;
char ob[MB+100],*r,stk[128];
int tp;
FastIO(){p=q=ib,r=ob,tp=0;}
~FastIO(){fwrite(ob,1,r-ob,stdout);}
char read_char() {
if(p==q){
p=ib,q=ib+fread(ib,1,MB,stdin);
if(p==q)return 0;
}
return *p++;
}
template<typename T>
void read_int(T& x) {
char c=read_char(),l=0;
for(x=0;!isdigit(c);c=read_char())l=c;
for(;isdigit(c);c=read_char())x=x*10-'0'+c;
if(l=='-')x=-x;
}
}IO;
int pri[N],cnt,mn[N],mx[N],phi[N];
bool stater[N],flag[N];
int qp(int a,int b,int p){
int ans=1;
while(b){
if(b&1) ans=1ll*ans*a%p;
b>>=1,a=1ll*a*a%p;
}
return ans;
}
void Eular(){
stater[1]=flag[1]=flag[2]=flag[4]=true;
phi[1]=1;
for(int i=2;i<N;i++){
if(!stater[i]){
pri[++cnt]=i;
phi[i]=i-1;
mn[i]=mx[i]=i;
if(i>2){
int x=i;
while(x<N){
flag[x]=true;
if(2*x<N) flag[2*x]=true;
if(x>(N/x)) break;
x*=x;
}
}
}
for(int j=1;pri[j]*i<N&&j<=cnt;j++){
int x=i*pri[j];
stater[x]=true;
mn[x]=pri[j];
if(i%pri[j]==0){
mx[x]=mx[i]*pri[j];
if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
else phi[x]=x/mn[x] * (mn[x]-1);
break;
}
else mx[x]=pri[j],phi[x]=phi[x/mn[x]]*phi[mn[x]];
}
}
}
int p[N],num;
void fenjie(int n){
num=0;
while(n>1) p[++num]=mn[n],n/=mx[n];
}
bool check(int g,int n){
if(__gcd(g,n)!=1) return false;
for(int i=1;i<=num;i++) if(qp(g,phi[n]/p[i],n)==1) return false;
return true;
}
int find(int n){
for(int i=1;i<n;i++) if(check(i,n)) return i;
}
int T,m,n,g,id[N],a[N],n1,b[N],n2,c[N],n3,mod;
bool zero,f[N];
ULL mi[N<<1];
int add(int x,int y){return (x+y)>=mod?(x+y-mod):x+y;}
struct BIT{
ULL c[N<<1];
void Init(){memset(c,0,sizeof c);}
void add(int i,ULL x){for(;i<=2*mod;i+=(i&-i)) c[i]+=x;}
ULL ask(int i){
ULL sum=0;
for(;i;i-=(i&-i)) sum+=c[i];
return sum;
}
void modify(int x){
x++;
add(x,mi[x-1]),add(x+mod,mi[x+mod-1]);
}
ULL query(int l,int r){
l++,r++;
return ask(r)-ask(l-1);
}
}Bit;
void Init(){
fenjie(phi[m]);
int g=find(m);
int x=1;
id[0]=m;
for(int i=1;i<=m-1;i++){
x=1ll*x*g%m;
id[x]=i%(m-1);
}
mod=m-1;
for(int i=1;i<=n1;i++) a[i]=id[a[i]];
for(int i=1;i<=n2;i++) b[i]=id[b[i]];
sort(a+1,a+n1+1);
n1=unique(a+1,a+n1+1)-a-1;
sort(b+1,b+n2+1);
for(int i=1;i<=n2;i++){
if(b[i]==m) break;
int j=i,len=0;
while(j<=n2&&b[j]==b[i]) j++,len++;
j--;
for(int k=1;k<=len;k<<=1) c[++n3]=1ll*b[i]*k%mod,len-=k;
if(len) c[++n3]=1ll*len*b[i]%mod;
i=j;
}
}
int pos[N],tot;
int work(){
int ans=0;
for(int i=1;i<=n1;i++){
if(a[i]==m) break;
f[a[i]]=true;
ans++;
Bit.modify(a[i]);
}
int l,r,res,mid,lst,x,C;
for(int i=1;i<=n3;i++){
lst=tot=0,C=c[i];
if(Bit.query(0,mod-1)*mi[C]==Bit.query(C,mod-1+C)) continue;
while(true){
l=lst,r=mod-1,res=-1;
while(l<=r){
mid=(l+r)>>1;
if(Bit.query(lst,mid)*mi[C]!=Bit.query(lst+C,mid+C)) res=mid,r=mid-1;
else l=mid+1;
}
if(res==-1) break;
if(f[res]) pos[++tot]=res;
lst=res+1;
}
ans+=tot;
for(int j=1;j<=tot;j++){
x=add(pos[j],C);
f[x]=true,Bit.modify(x);
}
}
return ans;
}
signed main(){
freopen("operation.in","r",stdin);
freopen("operation.out","w",stdout);
mi[0]=1;
for(int i=1;i<N*2;i++) mi[i]=mi[i-1]*Base;
Eular();
IO.read_int(T);
while(T--){
IO.read_int(m),IO.read_int(n),n1=n2=0;
zero=false;
int op,x;
for(int i=1;i<=n;i++){
IO.read_int(op),IO.read_int(x);
if(op==0) a[++n1]=x;
else b[++n2]=x;
zero|=(x==0);
}
if(!n1){
printf("%d\n",m-1);
continue;
}
Init();
printf("%d\n",m-(work()+zero));
if(T) memset(f,0,sizeof f),Bit.Init();
}
return 0;
}
C.排列
原题:[PA 2022] Chodzenie po linie
题意
给定一个长度为 \(n\) 的排列 \(p\) 由它生成一张无向图 \(G\),两个点 \(i,j\) 之间有边当且仅当 \(i<j\) 且 \(p_i>p_j\),边权均为 \(1\),记 \(dis(x,y)\) 表示 \(G\) 中两点间的最短路,特殊的,如果 \(x,y\) 不连通 \(dis(x,y)=0\),请对每个 \(x\in [1,n]\) 求 \(\sum_{y=1}^n dis(x,y)\)。
数据范围: \(1\le n \le 2\times 10^5\)。
题解
首先解决连通性问题,不难证明,如果有一个 \(i\) 满足 \(\forall j \in [1,i],p_j < p_i\) 那 \([1,i]\) 和 \([i+1,n]\) 之间一定不可能相互到达,找出每个这样的 \(i\) 就可以把原排列划分成若干段连通的区间。
下面假设整个排列连通。
考虑如何计算单个 \(i\) 的答案,我们只考虑左边对 \(i\) 的贡献,右半边只需要把排列翻转再做一次即可。
直接算最短路显然不好算,考虑改为计算有多少个最短路 \(>=t\),那么答案就是:\(\sum_{t\ge 1} \sum_j [dis(i,j)\ge t]\)。
首先 \(t=1\) 答案显然是 \(i-1\),对于 \(t>1\) 的情况,我们把 \((i,p_i)\) 看成一个点放到平面上考虑。
那么显然下图中红色矩形内的点可以被一步到达,左下角的矩形内的点都无法被到达,他们满足 \(j<i,p_j<p_i\)。
![图片[2]-NOI2025 广东省队集训题解-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/05/8165911705700182492.png)
我们找到矩形 \(A\) 中最靠左的点和矩形 \(B\) 中最靠右的点,不难发现前者可以一步到达绿色矩形内的点,后者可以一步到达黄色矩形内的点,那么此时左下角那个更小的矩形就是 \(dis\ge 3\) 的点。
![图片[3]-NOI2025 广东省队集训题解-牛翰网](https://niuimg.niucores.com/wp-content/uploads/2025/05/1093266203428800692.png)
同理,我们继续找到黄色矩形中最靠左的点和绿色矩形中最靠下的点,就可以得到 \(dis\ge 4\) 的点的范围了,即图中的紫色矩形。
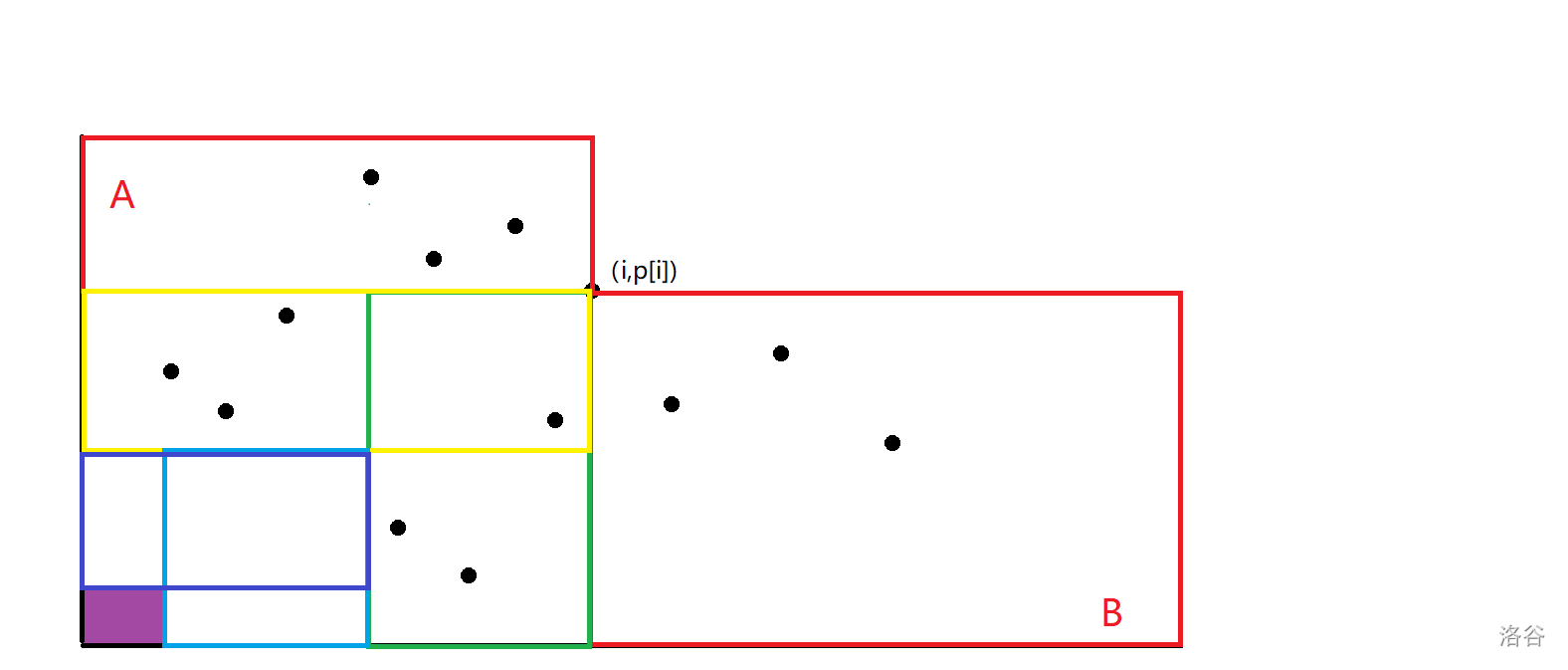
会发现对于每个 \(t\) 的答案都是一个矩形求和,设 \((a_t,b_t)\) 表示 \(t\) 的答案是所有满足 \(j<a_t,p_j<p_{b_t}\) 的 \(j\) 的数量,那么根据上述过程容易发现,\((a_2,b_2)=(i,i)\),\((a_{t+1},b_{t+1})=(ls_{b_t},rs_{a_t})\),其中 \(ls_x\) 表示 \(x\) 能到达的最靠左的点,\(rs_x\) 表示 \(x\) 能到达的最靠下的点。所以你只要预处理二维前缀和就可以做到 \(O(n^2)\)。
如果把 \((x,y)\) 向 \((ls_y,rs_x)\) 连有向边,会连出一个内向树森林,我们要求的东西就是一条根链上每个点矩形和的总和,
接下来我们证明这个森林中所有会用到的点是 \(O(n\sqrt{n})\) 级别的。
根据点的生成过程不难发现有用的点 \((x,y)\) 一定满足 \(x<y,p_x>p_y\)(除了那 \(n\) 个形如 \((i,i)\) 的点,但是他们的数量可以忽略)。所以对于一个 \(x\),我们找出所有满足 \(y>x,p_y<p_x\) 的 \(y\),假设按照 \(p_y\) 从小到大排序后是 \(y_1,y_2,y_3,…\)。对于一个点 \((x,y_k)\) 如果 \(k\le \sqrt{n}\) 我们称他为好点,否则为坏点。显然好点的数量是 \(O(n\sqrt{n})\)。对于坏点 \((x,y_k)\) 他的下一步会跳到 \((ls_{y_k},y_1)\),显然有 \(ls_{y_k}\le x,p_{y_1}\le p_{y_k} – \sqrt{n}\),因此一个坏点每跳一次都会使 \(x+p_y\) 减少至少 \(O(\sqrt{n})\),而 \(x+p_y\) 显然不会增加,因此所有会跳到的坏点的数量是 \(O(n\sqrt{n})\) 的,而它一定大于等于有用的坏点数量。证毕。
有了这个结论之后就好做很多了,假设我们已经得到了这 \(O(n\sqrt{n})\) 个点,那么就有 \(O(n)\) 次单点加,\(O(n\sqrt{n})\) 次矩形求和,我们对 \(x\) 扫描线,维护 \(y\) 这一维,变成区间求和,用分块平衡一下做到 \(O(n\sqrt{n})\)。同时注意到树上 \((x,y)\) 的父亲 \((x’,y’)\) 一定满足 \(x’\le x\) ,也就是说父亲会先被计算到,所以我们不需要去把树建出来直接让儿子继承父亲的贡献就可以得到儿子的答案了。
接下来说如和得到所有有用的点。
实测你对每个 \((i,i)\) 暴力的跑出所有点并用 unordered_map 记录是否被访问过会被卡常。(反正我被卡了)
因为 \((x,y)\) 的父亲 \((x’,y’)\) 一定满足 \(x’\le x\),所以我们可以按照 \(x\) 从大往小来加点,初始时每个 \(x\) 的队列中只有 \((x,x)\) 一个点,当扫到 \(x\) 时,遍历他队列中的每个点 \((x,y)\) 把 \((ls_y,rs_x)\) 加入到 \(ls_y\) 的集合中,同时容易证明 \(j\) 越小 \(p_{rs_j}\) 一定越小,也就是说此时的 \(rs_x\) 一定是 \(ls_y\) 队列中 \(p\) 值最小的(初始的那一个元素特判即可),因此我们直接看队尾和放进去的数是否一样即可去重。
总复杂度 \(O(n\sqrt{n})\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
using namespace std;
const int N=2e5+5,B=450;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
namespace Work{
int n,p[N];
LL res[N];
struct SegmentTree{
struct node{
int l,r,ming;
}t[N<<2];
void pushup(int p){
t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming);
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].ming=n+1;
if(l==r) return;
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
}
void change(int p,int x,int val){
if(t[p].l==t[p].r){
t[p].ming=val;
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x,val);
else change(p<<1|1,x,val);
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r) return t[p].ming;
int res=n+1,mid=(t[p].l+t[p].r)>>1;
if(l<=mid) res=min(res,ask(p<<1,l,r));
if(r>mid) res=min(res,ask(p<<1|1,l,r));
return res;
}
}Seg;
struct DS{
int L[N],R[N],id[N],s[N],pre[B];
void Init(){
for(int i=1;i<=n;i++){
id[i]=(i+B-1)/B,R[id[i]]=i;
if(i%B==1) L[id[i]]=i;
s[i]=0;
}
for(int i=1;i<=id[n];i++) pre[i]=0;
}
void add(int x,int val){
for(int i=x;i<=R[id[x]];i++) s[i]+=val;
for(int i=id[x];i<=id[n];i++) pre[i]+=val;
}
int query(int l,int r){
if(l==L[id[l]]) return s[r];
else return s[r]-s[l-1];
}
int ask(int l,int r){
if(l>r) return 0;
if(id[l]==id[r]) return query(l,r);
return query(l,R[id[l]])+query(L[id[r]],r)+pre[id[r]-1]-pre[id[l]];
}
}ds;
int ls[N],rs[N];
struct P{
int y,fa;
LL ans;
};
vector<P> v[N];
void Init(){
for(int i=1;i<=n;i++) v[i].clear();
Seg.build(1,1,n);
ds.Init();
}
void work(int op){
Init();
for(int i=1;i<=n;i++){
Seg.change(1,p[i],i);
ls[i]=Seg.ask(1,p[i],n);
}
int pos=n;
for(int i=n;i>=1;i--){
if(p[i]<p[pos]) pos=i;
rs[i]=pos;
}
for(int x=1;x<=n;x++) v[x].push_back({x,0,0});
for(int x=n;x>=1;x--){
for(int i=0;i<v[x].size();i++){
int y=v[x][i].y;
if(rs[x]!=v[ls[y]].back().y&&rs[x]!=ls[y]) v[ls[y]].push_back({rs[x],0,0});
v[x][i].fa=v[ls[y]].size()-1;
}
}
for(int x=1;x<=n;x++){
//此时 v[x] 中的 y 是按照 p[y] 降序排的,但是在计算答案的时候父亲的 p[y'] <= 当前节点的 p[y],需要在之前被计算到,所以要把 y 按照 p[y] 升序排。
for(int i=v[x].size()-1;i>=0;i--){
int y=v[x][i].y;
v[x][i].ans=v[ls[y]][v[x][i].fa].ans+ds.ask(1,p[y]-1);
if(x==y){
if(op) res[n-x+1]+=v[x][i].ans+x-1;
else res[x]+=v[x][i].ans+x-1;
}
}
ds.add(p[x],1);
}
}
void Main(){
for(int i=1;i<=n;i++) res[i]=0;
work(0);
for(int i=1;i<=n;i++) p[i]=n-p[i]+1;
reverse(p+1,p+n+1);
work(1);
for(int i=1;i<=n;i++) printf("%lld ",res[i]);
}
}
int n,a[N];
signed main(){
freopen("permutation.in","r",stdin);
freopen("permutation.out","w",stdout);
n=read();
vector<int> pos;
int maxn=0;
for(int i=1;i<=n;i++){
a[i]=read();
maxn=max(maxn,a[i]);
if(maxn==i) pos.push_back(i);
}
int lst=1;
for(int x:pos){
Work::n=0;
for(int i=lst;i<=x;i++) Work::p[++Work::n]=a[i]-(lst-1);
lst=x+1;
Work::Main();
}
puts("");
return 0;
}
Day2 模拟赛
A.火力全开
题意
有 \(n\) 个敌人,每个敌人有两个属性 \(a_i\) 和 \(b_i\) 表示血条和抗爆能力。
你可以进行若干轮攻击,每次选择一下两种方式中的一种:
- 指定一名敌人,花费 \(1\) 的代价,并对他造成 \(1\) 点真实伤害。
- 用一枚炸弹,对所有敌人造成一次爆炸伤害。
其中对于第 2 中攻击方式,你初始有 \(m\) 枚炸弹,第 \(i\) 枚炸弹的代价是 \(c_i\),爆炸伤害是 \(d_i\),每次你都可以选择一枚使用,每枚炸弹只能使用一次。
当第 \(i\) 个敌人受到 \(a_i\) 点真实伤害,或者受到 \(k\) 次大于等于 \(b_i\) 的爆炸伤害,他就会死亡。
现在你需要求出最少花费多少的代价可以杀死所有敌人。
当然这太简单了,所以你先还需要支持 \(q\) 次修改,每次修改形如 op x y z,如果 \(op=1\) 表示令 \(y \to a_x,z \to b_x\),否则表示令 \(y\to c_x,z\to d_x\)。
你需要在每次修改完之后求出答案,修改之间不独立。
数据范围:\(1\le n,m,q\le 2.5\times 10^5,1\le k \le 10^4,kq\le 5\times 10^5,1\le a_i,b_i,c_i,d_i,y,z \le 10^9\)。
题解
首先有一个显然的贪心,枚举 \(k\) 个炮弹中最小的爆炸伤害 \(d\),那么此时的总代价是 \(\sum_{b_i>d}a_i + S(k,d)\),\(S(k,d)\) 表示爆炸伤害 \(\ge d\) 的炮弹中代价前 \(k\) 小的和。
但是这个贪心不太好直接维护。
注意到数据范围中有一个很特殊的 \(kq\le 5\times 10^5\),这启发我们去维护某些大小为 \(O(k)\) 的信息。
先把所有 \(d_i\) 以及 \(op=2\) 时的 \(z\) 离散化,建立值域线段树。
对于线段树上的每个节点 \(p\),我们去维护 \(mn_{p,i}\) 表示 \(p\) 所代表的区间中代价第 \(i\) 小的炮弹的代价,以及 \(f_{p,i}\) 表示从区间中选出 \(i\) 枚炸弹时的最小代价总和。那么答案就是 \(\min(\sum_{i=1}^n a_i,f_{1,k})\)。容易发现这两个数组的长度都是 \(O(\min(k,siz))\) 的,\(siz\) 表示 \(p\) 所代表的区间中实际有的炮弹数量。
考虑 \(f\) 的转移:
- \(i\) 个炮弹全来自右儿子:\(f_{rs,i} \to f_{p,i}\)。
- \(j\) 个炮弹来自左儿子,其余来自右儿子:\(f_{ls,j} + suma_{rs} + pre_{rs,i-j} \to f_{p,i}\),\(suma\) 表示区间中的敌人的 \(\sum a_i\),\(pre_{rs,i}=\sum_{j=1}^i mn_{rs,j}\)。
对于第 2 个转移,\(suma_{rs}\) 是常量不去管,记 \(w(j,i)=f_{ls,j} + pre_{rs,i-j}\),容易证明他满足四边形不等式,所以第 2 个转移可以决策单调性优化到 \(O(\min(siz,k)\log \min(siz,k))\)。
故线段树的 pushup 的复杂度是 \(O(\min(siz,k)\log \min(siz,k))\)。
对于修改操作就是一个简单的单点修改,不赘述。
关于总时空复杂度(\(n\) 代表线段树值域大小):
- 空间复杂度:因为线段树的每个节点开的数组大小不是 \(O(k)\) 而是 \(O(\min(siz,k))\) 所以线段树的每一层的空间是 \(O(n)\) 的,整颗线段树的总空间是 \(O(n\log n)\)。
- 时间复杂度:类似的可以证明线段树建树的复杂度是 \(O(n\log k \log n)\),而一次修改操作会
pushup\(O(\log n)\) 次,所以修改的总复杂度是 \(O(qk\log k\log n)\)。
code
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=250000+5;
const LL inf=3e14;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,T,k,a[N],b[N],c[N],d[N],dis[N<<1],cnt;
LL Sum;
int Dis(int x){return lower_bound(dis+1,dis+cnt+1,x)-dis;}
struct Que{
int op,x,y,z;
}q[N];
vector<int> v[2][N<<1];
struct SegmentTree{
struct node{
int l,r,siz;
LL sum;
vector<LL> mn,pre,f;
void Init(){
siz=min(k,(int)v[0][l].size()),sum=0;
mn.resize(siz+1),f.resize(siz+1),pre.resize(siz+1);
sort(v[0][l].begin(),v[0][l].end(),[&](int x,int y){return c[x]<c[y];}); //注意要先对 vector 排序在赋值给 mn,而不能先赋值再对 mn 排序
for(int i=0;i<siz;i++) mn[i+1]=c[v[0][l][i]];
for(int id:v[1][l]) sum+=a[id];
f[0]=sum;
for(int i=1;i<=siz;i++) f[i]=f[i-1]+mn[i],pre[i]=pre[i-1]+mn[i];
}
}t[N<<4];
LL Pre(int p,int x){ return (x<=t[p].siz)?t[p].pre[x]:inf; }
void solve(int p,int l,int r,int L,int R){
if(l>r) return;
int mid=(l+r)>>1,opt=L,ls=p<<1,rs=p<<1|1;
LL res=t[rs].sum+t[ls].f[L]+Pre(rs,mid-L);
for(int i=L+1;i<=min(R,mid);i++){
if(t[rs].sum+t[ls].f[i]+Pre(rs,mid-i)<res){
opt=i;
res=t[rs].sum+t[ls].f[i]+Pre(rs,mid-i);
}
}
t[p].f[mid]=res;
solve(p,l,mid-1,L,opt),solve(p,mid+1,r,opt,R);
}
void pushup(int p){
int ls=p<<1,rs=p<<1|1;
t[p].siz=min(k,t[ls].siz+t[rs].siz);
t[p].sum=t[ls].sum+t[rs].sum;
t[p].mn.resize(t[p].siz+1),t[p].pre.resize(t[p].siz+1),t[p].f.resize(t[p].siz+1);
int i=1,j=1;
for(int x=1;x<=t[p].siz;x++){
if(i<=t[ls].siz&&(j>t[rs].siz||t[ls].mn[i]<t[rs].mn[j])) t[p].mn[x]=t[ls].mn[i++];
else t[p].mn[x]=t[rs].mn[j++];
t[p].pre[x]=t[p].pre[x-1]+t[p].mn[x];
}
solve(p,0,t[p].siz,0,t[ls].siz);
for(int i=0;i<=min(t[rs].siz,t[p].siz);i++) t[p].f[i]=min(t[p].f[i],t[rs].f[i]);
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].Init();
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
void update(int p,int x){
if(x==0) return;
if(t[p].l==t[p].r){
t[p].Init();
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) update(p<<1,x);
else update(p<<1|1,x);
pushup(p);
}
}Seg;
void Init(){
sort(dis+1,dis+cnt+1);
cnt=unique(dis+1,dis+cnt+1)-dis-1;
for(int i=1;i<=n;i++) b[i]=Dis(b[i])-1,v[1][b[i]].push_back(i);
for(int i=1;i<=m;i++) d[i]=Dis(d[i]),v[0][d[i]].push_back(i);
for(int i=1;i<=T;i++){
if(q[i].op==1) q[i].z=Dis(q[i].z)-1;
else q[i].z=Dis(q[i].z);
}
Seg.build(1,1,cnt);
}
void Add(int x,int op,int pos){
v[op][pos].push_back(x);
Seg.update(1,pos);
}
void Del(int x,int op,int pos){
for(vector<int>::iterator it=v[op][pos].begin();it!=v[op][pos].end();++it){
if((*it)==x){
v[op][pos].erase(it);
break;
}
}
Seg.update(1,pos);
}
signed main(){
freopen("fire.in","r",stdin);
freopen("fire.out","w",stdout);
n=read(),m=read(),T=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read(),b[i]=read(),Sum+=a[i];
for(int i=1;i<=m;i++) c[i]=read(),d[i]=read(),dis[++cnt]=d[i];
for(int i=1;i<=T;i++){
int op=read(),x=read(),y=read(),z=read();
q[i]={op,x,y,z};
if(op==2) dis[++cnt]=z;
}
Init();
for(int i=1;i<=T;i++){
if(q[i].op==1){
Del(q[i].x,1,b[q[i].x]);
Sum-=a[q[i].x];
a[q[i].x]=q[i].y,b[q[i].x]=q[i].z;
Sum+=a[q[i].x];
Add(q[i].x,1,q[i].z);
}
else{
Del(q[i].x,0,d[q[i].x]);
c[q[i].x]=q[i].y,d[q[i].x]=q[i].z;
Add(q[i].x,0,q[i].z);
}
printf("%lld\n",min(Sum,Seg.t[1].f[k])); //注意 Seg.t[1].sum!=Sum
}
return 0;
}
闲话
关于我大样例没过,结果一交 AC 这件事。数据没有大样例强是这样的。(这个数据甚至还是在赛时加了两个 hack 的)。
B.异或症测试 3
原题:The Best Problem of 2021
题意
给定一个大小为 \(n\) 的集合 \(B\) 和一个数 \(X\),问集合 \(S=\{1,2,…,X \}\) 有多少非空子集 \(T\) 满足 \(B\) 是 \(T\) 的线性基。对 \(998244353\) 取模。
称 \(B\) 是 \(T\) 的线性基当且仅当 \(T\) 中所有元素都可以由 \(B\) 中的若干元素异或得到,且 \(B\) 是所有满足条件的集合中大小最小的。(当然一个集合的线性基可能不止一个)
\(B\) 中的数以及 \(X\) 都以一个 \(m\) 位二进制数的形式给出。
数据范围:\(1\le n,m\le 2\times 10^3\)。
C.树上邻邻域数点
题意
这是一道交互题。
给定一课 \(n\) 个点的树,节点编号 \(\in [0,n-1]\),每个点有一个未知的属于 \([0,31]\) 的点权,每次你可以向交互库询问 \((x,d,v)\) 表示树上与 \(x\) 距离恰好为 \(d\) 的点中有多少个点的点权 \(\le v\),同时你需要保证每次询问的 \(v\) 不小于一个的给定的数 \(L\)。
你需要在 \(2.5 \times 10^5\) 次询问内求出每个点的点权。
数据范围:\(n=50000,0\le L\le 2\)。
附上附件中交互库的使用方法:
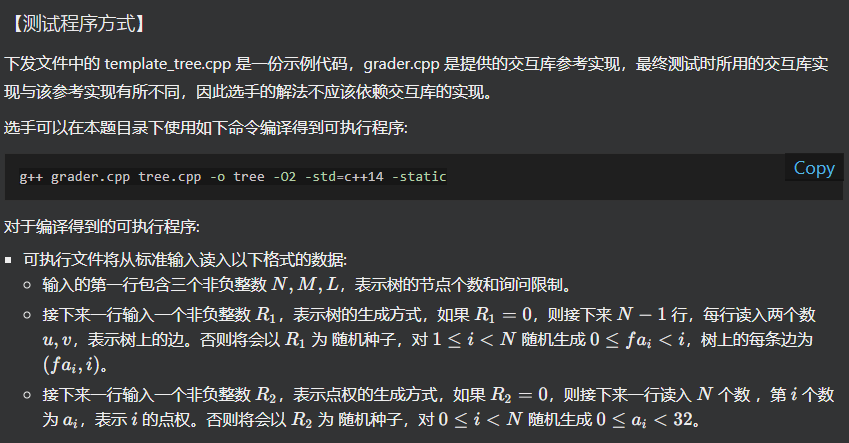
Day4 模拟赛
A.树
原题:Equal Trees。
题意
给你两棵编号从 \(1\) 到 \(n\),以 \(1\) 为根的有根树,定义一次操作形如:选择一棵树以及一个点 \(x\)(\(x\ne 1\)),把 \(x\) 的所有儿子接到 \(fa_x\) 上,并删除 \(x\) 以及和他相连的所有边。
定义两棵有根树是相同的当且仅当他们节点编号的集合相同且相同编号的点的父亲在两棵树中的编号相同,问最少操作几次才能使两棵树变成相同的。
注意:相同 \(\ne\) 同构。
数据范围:\(1\le n \le 40\)。
题解
正难则反,考虑求出最多保留多少点。
容易发现一个保留的点集 \(S\) 合法当且仅当不存在 \(x,y \in S\),且 \(x\) 在其中一棵树上是 \(y\) 的祖先但是在另一棵树上不是(\(y\) 是 \(x\) 的祖先同理)。
所以我们按照这个规则连边,答案就是这张无向图上的最大独立集。
因为 \(n\) 很小,所以 meet in the middle 即可,我的复杂度是 \(O(n2^{\frac{n}{2}})\)。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
using namespace std;
const int N=(1<<20)+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,fa[2][50],tmp[2][50],dep[2][50];
vector<int> G[2][50];
void dfs(int u,int op){
dep[op][u]=dep[op][fa[op][u]]+1;
for(int v:G[op][u]){
if(v==fa[op][u]) continue;
fa[op][v]=u;
dfs(v,op);
}
}
int LCA(int x,int y,int op){
if(dep[op][x]>dep[op][y]) swap(x,y);
while(dep[op][y]>dep[op][x]) y=fa[op][y];
while(x!=y) x=fa[op][x],y=fa[op][y];
return x;
}
struct Graph{
int tot,head[50],to[2000],Next[2000];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
bool flag[50],stater[50];
int f[N],g[N];
void dfs(int u,int Max,int cnt){
if(u==Max+1){
if(Max==n/2){
int S=0;
for(int i=n/2+1;i<=n;i++) if(!flag[i]) S|=(1<<(i-n/2-1));
f[S]=max(f[S],cnt);
}
else{
int S=0;
for(int i=n/2+1;i<=n;i++) if(stater[i]) S|=(1<<(i-n/2-1));
g[S]=max(g[S],cnt);
}
return;
}
dfs(u+1,Max,cnt);
if(!flag[u]){
vector<int> vec;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(!flag[v]) vec.push_back(v),flag[v]=true;
}
stater[u]=true;
dfs(u+1,Max,cnt+1);
for(int v:vec) flag[v]=false;
stater[u]=false;
}
}
void work(){
dfs(1,n/2,0),dfs(n/2+1,n,0);
for(int i=0;i<=n-n/2-1;i++){
for(int S=0;S<(1<<(n-n/2));S++){
if(S>>i&1){
g[S]=max(g[S],g[S^(1<<i)]);
}
}
}
int ans=0;
for(int S=0;S<(1<<(n-n/2));S++) ans=max(ans,f[S]+g[S]);
printf("%d\n",2*n-2*ans);
}
}T;
signed main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
n=read();
for(int op=0;op<=1;op++)
for(int i=1;i<n;i++){
int u=read(),v=read();
G[op][u].push_back(v),G[op][v].push_back(u);
}
dfs(1,0),dfs(1,1);
for(int i=2;i<=n;i++){
for(int j=i+1;j<=n;j++){
int x=LCA(i,j,0),y=LCA(i,j,1);
if((x==i&&y!=i)||(x==j&&y!=j)||(y==i&&x!=i)||(y==j&&x!=j)){
T.add(i,j),T.add(j,i);
}
}
}
T.work();
return 0;
}
B.序列
原题:[ARC066F] Contest with Drinks Hard
题意
给你一个长度为 \(n\) 的序列 \(a\),和一个正整数 \(C\) 求:
\[\max_{S\in \{1,2,3,…,n\}}((\sum_{1\le l\le r\le n} \prod_{i=l}^r [i \in S])C – \sum_{i\in S} a_i) \]
你还需要支持 \(m\) 次修改,每次修改形如 x,y 表示将 \(a_x\) 修改为 \(y\) 之后的答案,修改之间互相独立。
你需要求出初始以及每次修改之后总共 \(m+1\) 个答案。
数据范围:\(1\le n \le 3\times 10^5,0\le m \le 3\times 10^5,1\le C\le 10^5,0\le a_i,y \le 10^9\)。
题解
不难设计出 DP,\(f_i\) 表示第 \(i\) 个数不选,前 \(i\) 个数的最大权值,转移如下:
\(f_i = \max_{j=0}^{i-1} (f_j+\binom{i-j}{2} C-pre_{i-1}+pre_j)\)。
不难发现可以用斜率优化把复杂度降下来。
对于单点修改的题目,有一个经典套路是把前后拼起来,所以我们再预处理出来 \(g_i\) 表示从后往前考虑,不选第 \(i\) 个数,\([i,n]\) 的最大权值,以及 \(h_x\) 表示选第 \(i\) 个数时全局的答案。
那么当把 \(a_x\) 修改为 \(y\) 则答案就是 \(\max(f_x+g_x,h_x+a_x-y)\)。
其中 \(g\) 的转移如 \(f\),主要看 \(h\) 的转移。
暴力转移的话,我们可以枚举 \(i\) 前面和后面第一个没选的位置 \(p\) 和 \(q\),那么有转移:\(f_p+g_q+\binom{q-p}{2} C-pre_{q-1}+pre_p\)。
注意到这个式子跟 \(i\) 无关,对 \(p,q\) 的要求只有先后顺序,所以考虑分治,具体的,当考虑到分治区间 \([l,r]\) 时,我们求出所有 \(p\in [l-1,mid],q\in [mid+1,r+1]\) 的 \(p,q\) 的贡献,以左半边为例,我们枚举 \(p\in [l-1,mid]\) 用斜率优化求出此时最优的答案,然后贡献到区间 \([p+1,mid]\)。右半边同理。
因为这个斜率优化的斜率是单调的,所以可以用双指针优化到线性,因此分治的复杂度是 \(O(n\log n)\)。
复杂度是 \(O(n\log n+q)\)。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,C,a[N],pre[N],f[N],g[N],h[N];
int st[N],top;
int x(int j,int op){return 2*C*j;}
int y(int j,int op){
if(op==0) return 2*f[j]+C*j*j+C*j+2*pre[j];
else return 2*g[j]+C*j*j-C*j-2*pre[j-1];
}
bool check(int mid,int k,int op){return (y(st[mid+1],op)-y(st[mid],op))<k*(x(st[mid+1],op)-x(st[mid],op));}
int find(int k){
int l=1,r=top-1,mid,res=top;
while(l<=r){
mid=(l+r)>>1;
if(check(mid,k,0)) r=mid-1,res=mid;
else l=mid+1;
}
return st[res];
}
void Insert(int i,int op){
while(top>=2 && (__int128)(y(st[top],op)-y(st[top-1],op)) * (x(i,op)-x(st[top],op)) < (__int128)(x(st[top],op)-x(st[top-1],op)) * (y(i,op)-y(st[top],op)) ) top--;
st[++top]=i;
}
void work(){
for(int i=1;i<=n+1;i++) pre[i]=pre[i-1]+a[i];
int ans=0;
f[0]=0;
top=0;
st[++top]=0;
for(int i=1;i<=n+1;i++){
int j=find(i);
f[i]=(y(j,0)-i*x(j,0)-C*i+C*i*i-2*pre[i-1])/2;
Insert(i,0);
}
}
int calc(int p,int q){return f[p]+g[q]+C*((q-p)*(q-p-1))/2-pre[q-1]+pre[p];}
int tmp[N];
void solve(int l,int r){
if(l==r){
h[l]=max(h[l],calc(l-1,r+1));
return;
}
int mid=(l+r)>>1;
top=0;
for(int p=l-1;p<=mid;p++) Insert(p,0);
for(int q=mid+2,R=top;q<=r+1;q++){
while(R>1&&check(R-1,q,0)) R--;
tmp[q-1]=calc(st[R],q);
}
for(int i=r-1;i>=mid+1;i--) tmp[i]=max(tmp[i+1],tmp[i]);
for(int i=mid+1;i<=r;i++) h[i]=max(h[i],tmp[i]);
top=0;
for(int q=mid+1;q<=r+1;q++) Insert(q,1);
for(int p=l-1,R=top;p<=mid-1;p++){
while(R>1&&check(R-1,p,1)) R--;
tmp[p+1]=calc(p,st[R]);
}
for(int i=l+1;i<=mid;i++) tmp[i]=max(tmp[i],tmp[i-1]);
for(int i=l;i<=mid;i++) h[i]=max(h[i],tmp[i]);
solve(l,mid),solve(mid+1,r);
}
void Init(){
work();
reverse(a+1,a+n+1);
for(int i=0;i<=n+1;i++) tmp[i]=f[i];
memset(f,0,sizeof f);
work();
reverse(a+1,a+n+1);
for(int i=0;i<=n+1;i++) g[i]=f[n+1-i];
for(int i=0;i<=n+1;i++) f[i]=tmp[i];
for(int i=1;i<=n+1;i++) pre[i]=pre[i-1]+a[i];
memset(h,-0x3f,sizeof h);
solve(1,n);
}
signed main(){
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
n=read(),m=read(),C=read();
for(int i=1;i<=n;i++) a[i]=read();
Init();
printf("%lld\n",f[n+1]);
for(int i=1;i<=m;i++){
int x=read(),y=read();
printf("%lld\n",max(f[x]+g[x],h[x]+a[x]-y));
}
return 0;
}
C.栈
有三个栈 \(S1,S2,S3\) 初始时 \(S1\) 自顶向下是 \(p_1,p_2,p_3,…,p_n\)(保证 \(p\) 是排列),\(S2,S3\) 为空,你可以进行若干次操作,每次操作有两种选择:
- 选择一个数 \(x\le A\) 把 \(S1\) 栈顶的 \(x\) 个数作为一个整体放入 \(S2\)。(即不改变相对顺序)。
- 选择一个数 \(x\le B\) 把 \(S2\) 栈顶的 \(x\) 个数作为一个整体放入 \(S3\)。(即不改变相对顺序)。
现在需要让 \(S3\) 自顶向下是 \(1,2,3,…n\) 请构造方案或报告无解。
多测。
数据范围:\(1\le \sum n\le 10^6,1\le A,B\le n\) 且 \(p\) 是排列。
Day5 模拟赛
A.图上的游戏
题意
小 A 和小 B 在一张 n 个点,m 条边的有向图上玩游戏,初始每个点有点权,范围在 \([0,2]\),两人轮流操作,小 A 先手。一个人操作时需要选择一个点权为 \(2\) 的点并把它的点权修改为 \(0/1\)。当图上没有点权为 \(2\) 的点时游戏结束,此时小 A 的分数为图上满足 \(c_u=0,c_v=1\) 的边 \(u\to v\) 的数量,小 B 的分数是 \(c_u=1,c_v=0\) 的边 \(u\to v\) 的数量。定义此时这张图的权值 \(Z=\) 小 A 的分数 \(-\) 小 B 的分数。小 A 希望让 \(Z\) 尽量大,小 B 希望让 \(Z\) 尽量小,问两人都绝顶聪明的情况下最终的 \(Z\) 会是多少。
观战者小 C 给了你一个长度为 \(n\) 的序列 \(c_1,c_2,…,c_n\) 以及一个数 \(m\),现在需要你对每个 \((N,M)\) 满足 \(1\le N \le n,1\le M \le m\) 求出:
对于一张 \(N\) 个点,每个点的初始点权是 \(c_1,c_2,…,c_N\) 的图,随机连 \(M\) 条边(允许重边和自环),所有 \(n^{2m}\) 种连边方案的最终权值 \(Z\) 的和。
数据范围:\(1\le n,m\le 50,c_i \in {0,1,2}\)。
题解
先考虑对于一张给定的图怎么求最终权值 \(Z\)。
由于现在贡献是在边上的,但是操作的是点,所以考虑把贡献转移到点上。具体的,对于一条边 \(u\to v\) 如果 \(c_u=0\) 就认为 \(u\) 在这条边的贡献是 \(1\) 否则是 \(-1\),如果 \(c_v=1\) 则认为 \(v\) 在这条边的贡献是 \(1\) 否则是 \(-1\)。
容易证明,此时图上所有点的贡献和就是 \(2Z\)。
而对于权值为 \(2\) 的点,设他的出度减去入度为 \(d\),那么如果它的点权修改为 \(0\),则贡献就是 \(d\),否则就是 \(-d\)。因为一个人操作的时候可以把点权为 \(2\) 的点修改为任意权值,因此如果小 A 操作,那最后这个点的贡献就是 \(|d|\),如果是小 B 操作,最后这个点的贡献就是 \(-|d|\)。因此两人的最优策略就是把所有权值为 \(2\) 的点按照 \(d\) 从大到小排序之后轮流取,奇数位贡献为 \(|d|\),偶数位贡献为 \(-|d|\)。
最后把原先点权就是 \(0/1\) 的点的贡献加上再除个 \(2\) 就是 \(Z\)。
根据这个计算方法,我们还可以发现一个性质,记 \(ans(N,M)\) 表示题目中要你求的对于 \((N,M)\) 的答案,那么那些原先权值就是 \(0/1\) 的点对 \(ans(N,M)\) 的贡献一定是 \(0\)。
这是因为这些点的贡献只跟他们的出度-入度有关,而我们只需要把一张图的边全部反向就可以使他们的贡献取反(容易证明如果这张图的边全部取反之后和原图是一样的,那么此时每个点的贡献一定全是 \(0\),因此不需要考虑这种情况)。
所以我们只需要考虑权值为 \(2\) 的点的贡献。
如果我们已经确定了每个点的出度和入度,那么方案数就是两个可重集排列数的乘积。所以 DP 过程就是给每个点确定出度和入度。
因为权值为 \(0/1\) 的点和权值为 \(2\) 的点是相对独立的,可以分开考虑。(权值为 \(0/1\) 的点虽然本身不产生贡献但是会对方案数产生影响)
对于权值为 \(0/1\) 的点,DP 是简单的,设 \(f_{i,j,k}\) 表示给 \(i\) 个点分配 \(j\) 个出度和 \(k\) 个入度的方案数,转移显然。
对于权值为 \(2\) 的点,注意到我们最开始的那个贪心过程要求我们对 \(|d|\) 从大到小排序,所以我们 DP 的时候需要按照 \(|d|\) 从大到小加入,不难发现这其实是一个高维背包,二元组 \((x,y)\)(\(x\) 表示出度,\(y\) 表示入度)就表示一个物品,我们需要按照 \(|x-y|\) 从大到小把物品加入背包。那么设 \(g_{i,j,u,v}\) 表示考虑到第 \(i\) 个物品,分配了 \(j\) 个点,\(u\) 个出度,\(v\) 个入度的贡献之和,为了辅助转移还需要记录 \(h_{i,j,u,v}\) 表示方案数。转移时就去枚举当前物品分配给了几个点。直接做是 \(O(n^2m^4)\),但是发现转移时有个调和级数,于是变成 \(O(n^2m^3\log m)\),稍微剪枝可过。
算答案的时候就是把两个 DP 数组合并一下。需要注意的是在算 \(g,h\) 时我们钦定了顺序,但实际上分配是随便分配的(钦定顺序只是为了方便计算贡献),所以方案数还需要乘上一个可重集排列数。
具体实现时就是把几个可重集排列数的分子分母拆开,分母放到 DP 里面,分子由于是定值在最后算答案的时候乘上即可。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
using namespace std;
const int N=50+5,mod=1e9+7,inv2=(mod+1)/2;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,c[N],fact[N],inv[N],cnt;
int f[N][N][N],g[2][N][N][N],h[2][N][N][N];
void add(int &x,int y){x+=y; if(x>=mod) x-=mod;}
int qp(int a,int b){
int ans=1;
while(b){
if(b&1) ans=1ll*ans*a%mod;
b>>=1,a=1ll*a*a%mod;
}
return ans;
}
struct node{
int x,y,d;
}a[N*N];
int val(int s1,int s2,int x){
if(s2&1){
if(s1&1) return mod-x;
return x;
}
return 0;
}
signed main(){
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
n=read(),m=read();
int c2=0;
for(int i=1;i<=n;i++) c[i]=read(),c2+=(c[i]==2);
fact[0]=1;
for(int i=1;i<=n;i++) fact[i]=1ll*fact[i-1]*i%mod;
inv[1]=inv[0]=1;
for(int i=2;i<=n;i++) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=1;i<=n;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
f[0][0][0]=1;
for(int i=1;i<=n-c2;i++)
for(int j=0;j<=m;j++)
for(int k=0;k<=m;k++){
for(int x=0;x<=j;x++)
for(int y=0;y<=k;y++)
add(f[i][j][k],1ll*f[i-1][j-x][k-y]*inv[x]%mod*inv[y]%mod);
}
for(int x=0;x<=m;x++) for(int y=0;y<=m;y++) a[++cnt]={x,y,abs(x-y)};
sort(a+1,a+cnt+1,[&](node u,node v){return u.d>v.d;});
h[0][0][0][0]=1;
for(int i=1;i<=cnt;i++){
memset(g[i&1],0,sizeof g[i&1]);
memset(h[i&1],0,sizeof h[i&1]);
int x=a[i].x,y=a[i].y,d=a[i].d;
for(int j=0;j<=c2;j++){
for(int u=0;u<=m;u++){
for(int v=0;v<=m;v++){
if(h[i&1^1][j][u][v]){
for(int k=0;j+k<=c2&&u+k*x<=m&&v+k*y<=m;k++){
int t1=1ll*qp(1ll*inv[x]*inv[y]%mod,k)*inv[k]%mod,t2=1ll*h[i&1^1][j][u][v]*t1%mod;
add(h[i&1][j+k][u+k*x][v+k*y],t2);
add(g[i&1][j+k][u+k*x][v+k*y],(1ll*g[i&1^1][j][u][v]*t1%mod+1ll*val(j,k,d)*t2%mod)%mod);
}
}
}
}
}
}
int num1=0,num2=0;
for(int i=1;i<=n;i++){
if(c[i]<2) num1++;
else num2++;
for(int M=1;M<=m;M++){
int ans=0;
for(int j=0;j<=M;j++){
for(int k=0;k<=M;k++){
add(ans,1ll*f[num1][j][k]*g[cnt&1][num2][M-j][M-k]%mod*fact[M]%mod*fact[M]%mod*fact[num2]%mod);
}
}
printf("%d ",1ll*ans*inv2%mod);
}
puts("");
}
return 0;
}
B.修理
原题:Занулити пiдвiдрiзок
题意
对于一个正整数序列 \(b\) 定义它的代价为最少的操作次数使他变成全 \(0\),一次操作有两种选择:
- 令 \(x\) 加一。
- 选择一个 \(b_i\) 并让他变成 \(b_i \oplus x\)。
其中 \(x\) 是一个初始为 \(0\) 的变量。
现在给定一个长度为 \(n\) 的序列 \(a\),有 \(Q\) 次询问,每次询问 \([l,r]\) 表示询问 \(a_l,a_{l+1},…,a_r\) 的代价。
强制在线。
数据范围:\(1\le n,Q \le 2\times 10^5,1\le a_i < 2^{60}\)。
提示: 根号是没有前途的。
题解
首先不难发现要把一个序列 \(b\) 变成全 \(0\),那么 \(x\) 至少要加到 \(2^k\),其中 \(k\) 是 \(b\) 中所有数的二进制最高位的最大值,否则没有办法把这一位消掉。然后对于那些 \(\le x\) 的 \(b_i\) 可以一步解决,对于那些 \(>x\) 的 \(b_i\) 可以两步解决。
所以区间 \([l,r]\) 的答案就是 \(r-l+1+\min_{x\ge 2^k}(x+\sum_{i=l}^r[a_i>x])\)。
发现会对 \(∑_{i=l}^r[a_i>x]\) 产生贡献的是 \([2^k+1,2^{k+1}-1]\) 中的数,所以我们可以把 \(a\) 序列按照二进制最高位分成 \(\log V\) 个子序列,每一个子序列单独考虑。
对于二进制最高位为 \(k\) 的子序列,可以把里面的数全都减去 \(2^k\),这样值域下界就变成了 \(1\),要求的就可以写成:\(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])\)。
发现当 \(x=0\) 时 \(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])\) 的值是 \(r-l+1\),所以 \(x\) 一定不超过 \(r-l+1\),也就只需要考虑那些值域在 \(O(n)\) 范围内的 \(a_i\)。(注意:虽然我们不去考虑那些 \(>n\) 的 \(a_i\) 但是他们对答案是有贡献的,在最后算答案的时候要加上。),下面默认所有 \(a_i\) 的值域是 \([1,n]\)。
进一步转换,\(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])=r-l+1+\min_{x\ge 0}(x-\sum_{i=l}^r[a_i\le x])=r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\)。所以我们只需要最小化 \(r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\),发现这个东西长得很像扩展 Hall 定理:
- 对于一个有 \(n\) 个左部点的二分图,他的最大匹配是 \(n-\max(|S|-|N(S)|)\)。
再看回要求的那个式子,我们可以按照下面这种方式构造一张二分图:所有左部点是 \(\{a_i|l\le i \le r\}\),所有右部点是 \(\{1,2,3,…,n\}\),\(a_i\) 和 \(j\) 之间有边当且仅当 \(j\le a_i\)。会发现上面那个式子的最优值肯定是取在 \(x\) 等于某个 \(a_i\) 的时候,所以在考虑 Hall 定理的时候只需要考虑那些 \(S=\{a_i|a_i\le x\},N(S)=\{1,2,3,…,x\}\) 的情况,那么容易发现此时 \(r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\) 刚刚好就是这张二分图的最大匹配。
因为这张二分图的性质很好,我们有一个很简单的贪心求最大匹配的方法:按任意顺序加入左部点,加入到 \(a_i\) 的时候贪心地把最大的还没匹配过的 \(x\le a_i\) 和 \(a_i\) 匹配。
观察这个过程,容易发现这个过程并不会使得已经匹配过的点失配,那么如果可以离线的话,我们可以统一处理右端点为 \(r\) 的询问,按顺序加入 \(a_r,a_{r-1},a_{r-2},…a_1\),然后对于一个询问 \([l,r]\) 就是看最终匹配的左部点里有多少个数的下标在 \([l,r]\) 范围内。于是就得到了一个 \(O(n^2)\) 的离线做法。
如果想要优化这个做法,那么我们就需要知道当 \(r\to r+1\) 时,左部点的匹配状态变成了什么样。
因为此时 \(a_{r+1}\) 的优先级是最高的,所以我们需要强制 \(a_{r+1}=val\) 和右部的 \(val\) 点匹配,如果能直接加那最好,但是如果右部点 \(val\) 已经被匹配了,这样会使得原先和右部点 \(val\) 匹配的左部点失配,于是我们就需要去找增广路,但显然这太麻烦了。
我们考虑用普通的 Hall 定理来判断一个匹配的合法性,如果一个匹配的左部点的集合为 \(S\),那么这个匹配合法当且仅当 \(\forall x \in [1,n],(x-\sum_{a_i\in S} [x\le a_i])\ge 0\)。我们记 \(w_x = x-\sum_{a_i\in S} [x\le a_i]\),那么我们需要让所有的 \(w\) 非负,当往匹配中加入一个 \(a_{r+1}\) 时,可能会使得某些 \(w_x<0\),我们找到其中最小的 \(x\) 满足 \(w_x<0\),那么我们就是要在所有 \(a_i\in S,a_i\le x\) 中挑一个出来从匹配中删掉,因为我们的贪心是按照下标从后往前加点的,所以我们需要把其中下标(注意不是值)最小的从匹配中删掉。
用一棵线段树维护 \(w_x\),用一棵线段树维护还没被删掉的左部点,上面的过程都可以轻松维护,把维护左部点的线段树可持久化就可以在线回答询问了。
因为我们分成的 \(\log V\) 个子序列的点数之和是 \(O(n)\) 的,所以总复杂度是 \(O((n+Q)\log n)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5,inf=N;
int n,Q,t,st[20][N];
LL a[N];
int RMQ(int l,int r){
int k=__lg(r-l+1);
return max(st[k][l],st[k][r-(1<<k)+1]);
}
struct SegmentTree{
#define ls(p) t[p].ls
#define rs(p) t[p].rs
int tot=0;
struct node{
int ls,rs,cnt;
PII ming;
}t[N*40];
void build(){
t[0].cnt=t[0].ls=t[0].rs=0;
t[0].ming={inf,inf};
}
int New(int p){
t[++tot]=t[p];
return tot;
}
void pushup(int p){
t[p].cnt=t[ls(p)].cnt+t[rs(p)].cnt;
t[p].ming=min(t[ls(p)].ming,t[rs(p)].ming);
}
int change(int p,int l,int r,int x,int val){
int q=New(p);
if(l==r){
t[q].ming={val,l};
t[q].cnt=(val!=inf);
return q;
}
int mid=(l+r)>>1;
if(x<=mid) t[q].ls=change(ls(q),l,mid,x,val);
else t[q].rs=change(rs(q),mid+1,r,x,val);
pushup(q);
return q;
}
PII find(int p,int l,int r,int R){
if(l==r) return t[p].ming;
int mid=(l+r)>>1;
if(t[ls(p)].ming.fi<=R) return find(ls(p),l,mid,R);
else return find(rs(p),mid+1,r,R);
}
int ask(int p,int l,int r,int L,int R){
if(L<=l&&r<=R) return t[p].cnt;
int mid=(l+r)>>1,sum=0;
if(L<=mid) sum+=ask(ls(p),l,mid,L,R);
if(R>mid) sum+=ask(rs(p),mid+1,r,L,R);
return sum;
}
}Seg;
struct SegmentTree2{
struct node{
int l,r,add;
PII ming;
void tag(int d){
ming.fi+=d,add+=d;
}
}t[N<<2];
void pushup(int p){t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming);}
void spread(int p){
if(t[p].add){
t[p<<1].tag(t[p].add);
t[p<<1|1].tag(t[p].add);
t[p].add=0;
}
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].add=0;
if(l==r){
t[p].ming={l,l};
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int l,int r,int d){
if(l<=t[p].l&&t[p].r<=r){
t[p].tag(d);
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p<<1,l,r,d);
if(r>mid) change(p<<1|1,l,r,d);
pushup(p);
}
}Seg2;
struct WORK{
int rt[N];
int cnt=0,m=0,id[N],a[N],ID[N];
void insert(int i,LL val){
if(val==0) return;
if(val<=n) id[++cnt]=i,a[cnt]=val;
else ID[++m]=i;
}
void work(int K){
if(!cnt&&!m) return;
Seg2.build(1,1,n);
for(int i=1;i<=cnt;i++){
rt[i]=Seg.change(rt[i-1],1,n,id[i],a[i]);
Seg2.change(1,a[i],n,-1);
if(Seg2.t[1].ming.fi<0){
PII x=Seg.find(rt[i],1,n,Seg2.t[1].ming.se);
rt[i]=Seg.change(rt[i],1,n,x.se,inf);
Seg2.change(1,x.fi,n,1);
}
}
}
int query(int l,int r){
int L,R=upper_bound(id+1,id+cnt+1,r)-id-1,ans=0;
if(id[R]>=l) ans+=Seg.ask(rt[R],1,n,l,r);
L=lower_bound(ID+1,ID+m+1,l)-ID,R=upper_bound(ID+1,ID+m+1,r)-ID-1;
return ans+R-L+1;
}
}T[65];
void Init(){
for(int t=1;t<=__lg(n);t++)
for(int i=1;i+(1<<t)-1<=n;i++)
st[t][i]=max(st[t-1][i],st[t-1][i+(1<<(t-1))]);
for(int i=1;i<=n;i++) T[__lg(a[i])].insert(i,a[i]-(1ll<<__lg(a[i])));
Seg.build();
for(int i=0;i<60;i++) T[i].work(i);
}
signed main(){
freopen("repair.in","r",stdin);
freopen("repair.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>Q>>t;
for(int i=1;i<=n;i++) cin>>a[i],st[0][i]=__lg(a[i]);
Init();
LL lstans=0;
while(Q--){
LL l,r; cin>>l>>r;
if(t==2) l^=lstans,r^=lstans;
if(l>r) swap(l,r);
int k=RMQ(l,r);
printf("%lld\n",(lstans=r-l+1+(1ll<<k)+T[k].query(l,r)));
}
return 0;
}
C.人员调度 2
题意
有一张有 \(n\) 个左部点和 \(n\) 个右部点的二分图,左部点 \(i\) 和右部点 \(j\) 之间有一条权值为 \(a_i + b_j + a_i \oplus b_j\) 的边。
同时这张图还有 \(m\) 条特殊边,一条特殊边 \((x,y,w)\) 表示左部点 \(x\) 和右部点 \(y\) 之间的边的边权在原来的基础上再加 \(w\)。
给定一个 \(K\),对于每个 \(k\in [1,K]\),求这张二分图大小为 \(k\) 的匹配中边权和最大的匹配,输出这个匹配的边权和即可。
数据范围: \(1\le n\le 10^5,0\le m \le 5\times 10^5,1\le K \le \min(300,n),0\le a_i,b_i < 2^{12},0\le w \le 10^5\) 保证不存在两条特殊边的 \(x,y\) 均相同。
时限: \(5s\)。
Day7 模拟赛
A.序列变换
题意
给一个长度为 \(n\) 下标从 \(1\) 开始的序列 \(a\),可以进行下列操作若干次:
- 选择一个区间 \([l,r]\),对于所有 \(i\in N,x\in \{0,1\},l+3i+x\le r\) 将 \(a_{l+3i+x}\) 加上 \((-1)^x\)。
问最少需要操作几次可以把 \(a\) 变成全 \(0\),无解输出 \(-1\)。
多测。
数据范围:\(T=30,n\le 3\times 10^4,|a_i|\le 10^{10}\)。
题解
神秘贪心题,完全不会做。
不妨设那些 \(i<1\) 或者 \(i>n\) 的 \(a_i\) 都是 \(0\),求出一个长度为 \(n+2\) 的序列 \(b\) 满足 \(b_i=a_i+a_{i-1}+a_{i-2}\)。
那么一次操作其实只有两种情况:
- \(l \equiv r \pmod 3\)(就是最后剩一个 \(+1\)):相当于是把 \(b_l+1,b_{r+1}+1,b_{r+2}+1\)。
- \(l \equiv r+1 \pmod 3\)(就是区间中 \(+1\) 和 \(-1\) 的数量相等)(\(l \equiv r-1 \pmod 3\) 的情况是等价的):相当于是把 \(b_l+1,b_{r+1}-1\)。
并且不难发现 1. 中的 \(l,r+1,r+2\) 模 \(3\) 两两不同余,2. 中的 \(l,r+1\) 模 \(3\) 同余。
目标就是把 \(b\) 全变成 \(0\)。
显然操作 1 一定会让 \(\sum b_i\) 加 \(3\),操作 2 不影响 \(\sum b_i\),因此操作 1 的操作次数已经确定了。并且如果 \(\sum b_i\) 不是 \(3\) 的倍数或者他 \(>0\) 就无解。
不妨先假设没有操作 2,此时有一个贪心做法。
从后往前考虑每个 \(i\),如果有 \(b_i,b_{i-1}<0\),在上面执行一次操作 1,但是此时我们不知道前面的 \(l\) 是哪个位置,不过我们可以知道 \(l\bmod 3\) 的值,所以我们先用一个变量存储,之后再去用。
如果当前的 \(b_i<0\) 但是 \(b_{i-1}=0\) 或者使用次数没有了,那么我们就从之前存的对应的变量中取出一些填到这个位置上。
现在加上操作 2。
会发现只有操作 1 的情况不能做有 \(b_i>0\) 的情况,但是有了操作 2 就可以做了,因为操作 \(2\) 可以把某个数 \(-1\)。
还是考虑贪心,从后往前考虑,假设当前考虑到 \(t\),且 \(b_i (i>t)\) 已经都是 \(0\) 了,分类讨论:
(1) \(b_t=0\):不管,跳过。
(2) \(b_t>0\):用操作 2,此时我们还是不去管前面的 \(l\) 到底是哪个位置,因为我们知道 \(l \equiv t \pmod 3\) 所以仍然用一个临时变量存下来,之后再用。
(3) \(b_t<0\):依次进行下列过程:
- 如果 \(b_{t-1}<0\),那么就一直用操作 1 直到操作次数用完了,或者 \(max(b_t,b_{t-1})=0\)。
- 如果 \(b_t\) 还是 \(<0\),我们先去用之前存下来的那些值填上去。
- 如果 \(b_t\) 仍然 \(<0\),那就没办法了,我们只能用操作 2 强行把 \(b_{t-1}\) 压下去变成和 \(b_t\) 一样,然后再用操作 1,显然此时如果操作次数不够了就无解了。
正确性的话感性理解一下就是对的。
\(O(Tn)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define int long long
using namespace std;
const int N=3e4+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int T,n,a[N],b[N];
int calc(int x,int y){
if(x!=0&&y!=0) return 0;
if(x!=1&&y!=1) return 1;
if(x!=2&&y!=2) return 2;
}
signed main(){
freopen("trans.in","r",stdin);
freopen("trans.out","w",stdout);
T=read(),n=read();
while(T--){
for(int i=1;i<=n;i++) a[i]=read();
a[n+1]=a[n+2]=0;
int sum=0;
for(int i=1;i<=n+2;i++) b[i]=a[i]+a[i-1]+((i==1)?0:a[i-2]),sum+=-b[i];
if(sum<0||sum%3!=0){
puts("-1");
continue;
}
int num[3]={0,0,0},cnt=sum/3,ans=0;
bool stater=true;
for(int i=n+2;i>=1;i--){
if(b[i]==0) continue;
if(b[i]>0) num[i%3]+=b[i],ans+=b[i];
else{
if(b[i-1]<0){
int deta=min(cnt,min(-b[i],-b[i-1]));
num[calc(i%3,(i-1)%3)]+=deta;
b[i]+=deta,b[i-1]+=deta;
cnt-=deta;
ans+=deta;
}
if(b[i]<0){
int deta=min(num[i%3],-b[i]);
num[i%3]-=deta;
b[i]+=deta;
}
if(b[i]<0){
if(!cnt||i==1){
stater=false;
break;
}
int deta=b[i-1]-b[i];
num[(i-1)%3]+=deta;
b[i-1]-=deta;
ans+=deta;
if(cnt<-b[i]){
stater=false;
break;
}
cnt-=-b[i];
num[calc(i%3,(i-1)%3)]+=-b[i];
ans+=-b[i];
b[i-1]+=-b[i],b[i]=0;
}
}
}
if(!stater) puts("-1");
else printf("%lld\n",ans);
}
return 0;
}
B.追忆
题意
给定一个数 \(n\) 和一个种子 \(seed\),由他生成一个 DAG,具体的生成过程如下:
- 对于所有 \(2\le i \le n\),在 \([1,i)\) 中随机两个数作为 \(a_i,b_i\),并由 \(i\) 向 \(a_i,b_i\) 连有向边。
给你 \(n-1\) 个询问,第 \(i\) 个询问 \(x_i\) 满足 \(1\le x_i \le i\),表示求 \(i+1\) 到 \(x_i\) 的最短路,到达不了答案就是 \(-1\)。
输出 \(\oplus_{i=1}^{n-1} (ans_i+2)\times i\)。
数据范围: \(1\le n \le 2\times 10^6\)。
题解
首先我们先证明一个点 \(x\) 可以到达的点的期望是 \(O(\sqrt{x})\) 的。
证明:\(<\sqrt{x}\) 的点有 \(O(\sqrt{x})\) 个,对于大于 \(O(\sqrt{x})\) 的点,如果我从 \(x\) 开始一直走,只走 \(>\sqrt{x}\) 的点,那么由图的生成过程可知,每走一步点的编号期望 \(\times \frac{1}{2}\),因此期望只能走 \(O(\log_2 \frac{x}{\sqrt{x}})\) 步,每一步有两种选择,总共最多走不超过 \(O(2^{\log_2 \frac{x}{\sqrt{x}}})=O(\sqrt{x})\) 个点。
所以我们设一个阈值 \(B\),暴力预处理出 \(O(B^2)\) 个点对间的最短路,时间复杂度是 \(O(\sum_{i=1}^B \sqrt{i})=O(B^{\frac{3}{2}})\)。
对于询问 \(dist(i+1,x_i)\),如果 \(i+1\le B\) 直接查表,否则从他开始 BFS,只走 \(> B\) 的点,走到 \(\le B\) 的点就直接查表之后返回。同理可以得到一次 BFS 的复杂度是 \(O(\frac{n}{B})\),因此回答询问的总复杂度是 \(O(\frac{n^2}{B})\)。
平衡一下,取 \(B=n^{\frac{4}{5}}\approx 10^5\),时间复杂度是 \(O(n^{\frac{6}{5}})\)。
但是注意到你开不了 \(O(B^2)\) 的数组,所以可以把要用到的询问离线下来之后统一处理。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e6+5,B=1e5;
int n,x[N],a[N],b[N],ans[N];
unsigned int seed;
unsigned shift(unsigned &a){
a^=a<<13;
a^=a>>7;
a^=a<<17;
return a;
}
void init(unsigned seed){
for(int i=2;i<=n;i++)
a[i]=shift(seed)%(i-1)+1,
b[i]=shift(seed)%(i-1)+1;
}
struct node{
int x,Dist,id;
};
vector<node> Que[B+5];
queue<int> Q;
int dist[B+5];
vector<int> vec;
void BFS(int s){
Q.push(s);
dist[s]=0;
while(Q.size()){
int u=Q.front(); Q.pop();
vec.emplace_back(u);
if(u==1) continue;
if(dist[a[u]]==n+5) dist[a[u]]=dist[u]+1,Q.push(a[u]);
if(dist[b[u]]==n+5) dist[b[u]]=dist[u]+1,Q.push(b[u]);
}
for(node que:Que[s]) ans[que.id]=min(ans[que.id],que.Dist+dist[que.x]);
for(int x:vec) dist[x]=n+5;
vec.clear();
}
void work(){
for(int i=1;i<=B;i++) dist[i]=n+5;
for(int i=1;i<=min(B,n);i++) BFS(i);
}
int BFS2(int s,int t){
queue<PII> Q;
Q.push({s,0});
while(Q.size()){
int u=Q.front().fi,Dist=Q.front().se; Q.pop();
int x=a[u],y=b[u];
if(x==t||y==t) return Dist+1;
if(x>B) Q.push({x,Dist+1});
else if(t<=B) Que[x].push_back({t,Dist+1,s-1});
if(y>B) Q.push({y,Dist+1});
else if(t<=B) Que[y].push_back({t,Dist+1,s-1});
}
return n+5;
}
signed main(){
freopen("recall.in","r",stdin);
freopen("recall.out","w",stdout);
scanf("%d%u",&n,&seed);
init(seed);
for(int i=1;i<n;i++) scanf("%d",&x[i]),ans[i]=n+5;
for(int i=1;i<n;i++){
if(i+1<=B) Que[i+1].push_back({x[i],0,i});
else ans[i]=BFS2(i+1,x[i]);
}
work();
LL res=0;
for(int i=1;i<n;i++){
if(ans[i]==n+5) ans[i]=-1;
res^=1ll*(ans[i]+2)*i;
}
printf("%lld\n",res);
return 0;
}
C.小方的疑惑
题意
有一个长度为 \(n\) 的非负整数序列 \(a\) 和一个长度为 \(n-1\) 的正整数序列 \(b\),其中 \(b_i\) 满足 \(1\le b_i \le i\)。
可以执行以下操作若干次:
- 选择一个 \(i\in [1,n)\),满足 \(a_{b_i}>0\),将 \(a_{b_i}\) 减去 \(1\),将 \(a_{i+1}\) 加上 \(1\)。
求有多少种本质不同的序列 \(a\) 可以被生成,对 \(10^9+7\) 取模。
数据范围:\(1\le n \le 8\times 10^3,0\le a_i \le 10^9\)。
Day8 模拟赛
A.平衡树
题意
有一棵 \(n\) 个点的无根树,每个点有点权 \(a_i\),其中有一些边是关键边,定义一条关键边的不平衡度为:删除这条边之后,分成的两棵子树的点权和的差的绝对值。定义一棵树的不平衡度为所有关键边的不平衡度的最大值。
\(Q\) 次询问,每次给出 \(k\) 条关键边以及两个非负整数 \(L,R\),一次操作定义为给一个点的点权 \(+1\),你至少操作 \(L\) 次,至多操作 \(R\) 次,问最终这棵树的不平衡度最小是多少。
数据范围:\(2\le n\le 3\times 10^5,1\le Q \le n,0\le a_i \le 10^6,0\le L,R \le 10^9,1\le k \le n-1,1\le \sum k \le n\)。
题解
首先不难证明如果有三条关键边在同一条链上,那么中间的那条一定没用,因为左右两边总有一条关键边的不平衡度比他大。
也就是说如果我们把不包含关键边的连通块缩成一个点,那么会得到一棵只含关键边的树,此时有用的关键边只有叶子连出去的边。
再换句话说,有用的关键边会形成一个菊花图。
所以只要考虑菊花图怎么做。
设此时所有点权之和是 \(S\),第 \(i\) 个叶子的点权为 \(s_i\),虽然可能会出现 \(2s_i>S\) 的情况,但容易证明这样的 \(s_i\) 只有至多一个,且他无论如何不会成为不平衡度最大的,所以可以认为每条边的不平衡度就是 \(S-2s_i\)。
显然要这个式子取到最大值需要让 \(s_i\) 尽可能小,所以我们先把 \(s_i\) 升序排序。
会发现我们每把最小值 \(+1\),不平衡度就会 \(-1\),但是当把最小值加到和次小值一样时,之后一旦要改变最小值就得至少操作 \(\ge 2\) 次,不会减少不平衡度,因此最优策略就是把最小值加到和次小值一样时就停手。
但是有了 \(L\) 的限制意味着我们在把最小值加到次小值之后可能还得继续加,直到加满 \(L\) 次。
不难 \(O(k)\) 地去模拟这个过程。
还有一个需要注意的点是,如果加到 \(L\) 次之后,场上刚刚好只有唯一的一个最小值,那么我们再花一次操作把这个最小值 \(+1\) 就能再让不平衡度 \(-1\),此时就要花费 \(L+1\) 次操作了。
最后就是怎么搞出这个菊花图,因为你不能直接像边双缩点那样把整棵树遍历一遍,但是可以先用 树状数组+dfn序 来判断出每条关键边是否有用,如果有用意味着这条关键边两侧的两棵子树一定有一棵不含任何关键边,那么这棵子树可以直接缩成一个点,且他就是这个菊花的一个叶子。
可能需要特判一下 \(k=1\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,T,a[N],tot,head[N],to[N<<1],Next[N<<1];
struct Edge{
int u,v;
}E[N];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int num,dfn[N],Size[N],fa[N],Sum[N];
void dfs(int u,int fa){
::fa[u]=fa;
dfn[u]=++num;
Size[u]=1;
Sum[u]=a[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs(v,u);
Sum[u]+=Sum[v];
Size[u]+=Size[v];
}
}
struct BIT{
int c[N];
int lowbit(int x){return x&(-x);}
void add(int i,int x){for(;i<=n;i+=lowbit(i)) c[i]+=x;}
int ask(int i,int sum=0){
for(;i;i-=lowbit(i)) sum+=c[i];
return sum;
}
int query(int x,int y){
return ask(y)-ask(x-1);
}
}Bit;
int k,L,R,cnt,id[N],s[N];
void work(){
sort(s+1,s+cnt+1);
int lst=L,i;
for(i=1;i<cnt;i++){
if(i*(s[i+1]-s[i])<lst) lst-=i*(s[i+1]-s[i]);
else break;
}
if(i==1){
int deta=min(R,s[i+1]-s[i]);
printf("%lld\n",(Sum[1]+deta)-2*(s[i]+deta));
return;
}
int x=lst/i,y=lst%i;
s[i]+=x;
if(y==i-1&&L<R) printf("%lld\n",(Sum[1]+L+1)-2*(s[i]+1));
else printf("%lld\n",(Sum[1]+L)-2*s[i]);
}
signed main(){
freopen("balance.in","r",stdin);
freopen("balance.out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
E[i]={u,v};
add(u,v),add(v,u);
}
dfs(1,0);
for(int i=1;i<n;i++) if(E[i].u==fa[E[i].v]) swap(E[i].u,E[i].v);
while(T--){
k=read(),L=read(),R=read();
for(int i=1;i<=k;i++){
id[i]=read();
Bit.add(dfn[E[id[i]].u],1);
}
if(k==1){
int x=Sum[E[id[1]].u],y=Sum[1]-x;
if(x>y) swap(x,y);
if(L<=y-x&&y-x<=R) puts("0");
else if(x+R<y) printf("%lld\n",y-x-R);
else if(x+L>y){
int z=y-x;
if((L-z)%2==0||L!=R) puts("0");
else puts("1");
}
}
else{
cnt=0;
for(int i=1;i<=k;i++){
int u=E[id[i]].u,num=Bit.query(dfn[u],dfn[u]+Size[u]-1);
if(k==1) s[++cnt]=min(Sum[u],Sum[1]-Sum[u]);
else if(num==1) s[++cnt]=Sum[u];
else if(num==k) s[++cnt]=Sum[1]-Sum[u];
}
work();
}
for(int i=1;i<=k;i++) Bit.add(dfn[E[id[i]].u],-1);
}
return 0;
}
B.上升树
题意
有一棵 \(n\) 个点的树,点有点权,一条路径的权值定义为其上面的点按顺序构成的序列的 \(LIS\)。
询问删除一个点后剩下的森林的所有路径的权值的最大值最小是多少,你只需要回答这个最小值而不需要输出具体删除哪个点。
数据范围:\(1\le n \le 10^5,1\le a_i \le n\)。
题解
首先指定根的情况下,求每个子树内的最大 \(LIS\) 是个经典问题,有多种解法,如线段树合并,长链剖分,dsu on tree 等等,选择你喜欢的方式实现即可,这里不赘述。(不会的可以看 [THUSC 2021] 白兰地厅的西瓜 或者 CF490F)。
下面默认用的是线段树合并,复杂度 \(O(n\log n)\)。
解法一
首先考虑一个树是链的情况的做法,我们先求出删掉中点之后左右两边哪个 \(LIS\) 大,那么显然要使 \(LIS\) 更小就要去更大的那一边删。每次取中点的话就需要求 \(O(\log n)\) 次 \(LIS\),总复杂度 \(O(n\log^2 n)\)。
考虑把他拓展到树上,我们先求出删去根之后的全局最长 \(LIS\),计入答案。然后看一下最长的 \(LIS\) 在哪棵子树中,那么同理要使 \(LIS\) 变得更小一定是去那棵子树里面删。我们每次像点分治那样选取重心作为根,那么就需要做 \(O(\log n)\) 次,总复杂度 \(O(n\log^2 n)\)。
解法二
考虑优化解法一,会发现其实递归到子树里面去删点之后没有必要把整棵树都重新做一遍,比如此时的根是 \(rt\),他有三棵子树 \(v_1,v_2,v_3\),最长 \(LIS\) 在 \(v_1\) 子树中,现在要递归到以 \(v_1\) 子树的重心 \(u\) 为根来求答案。
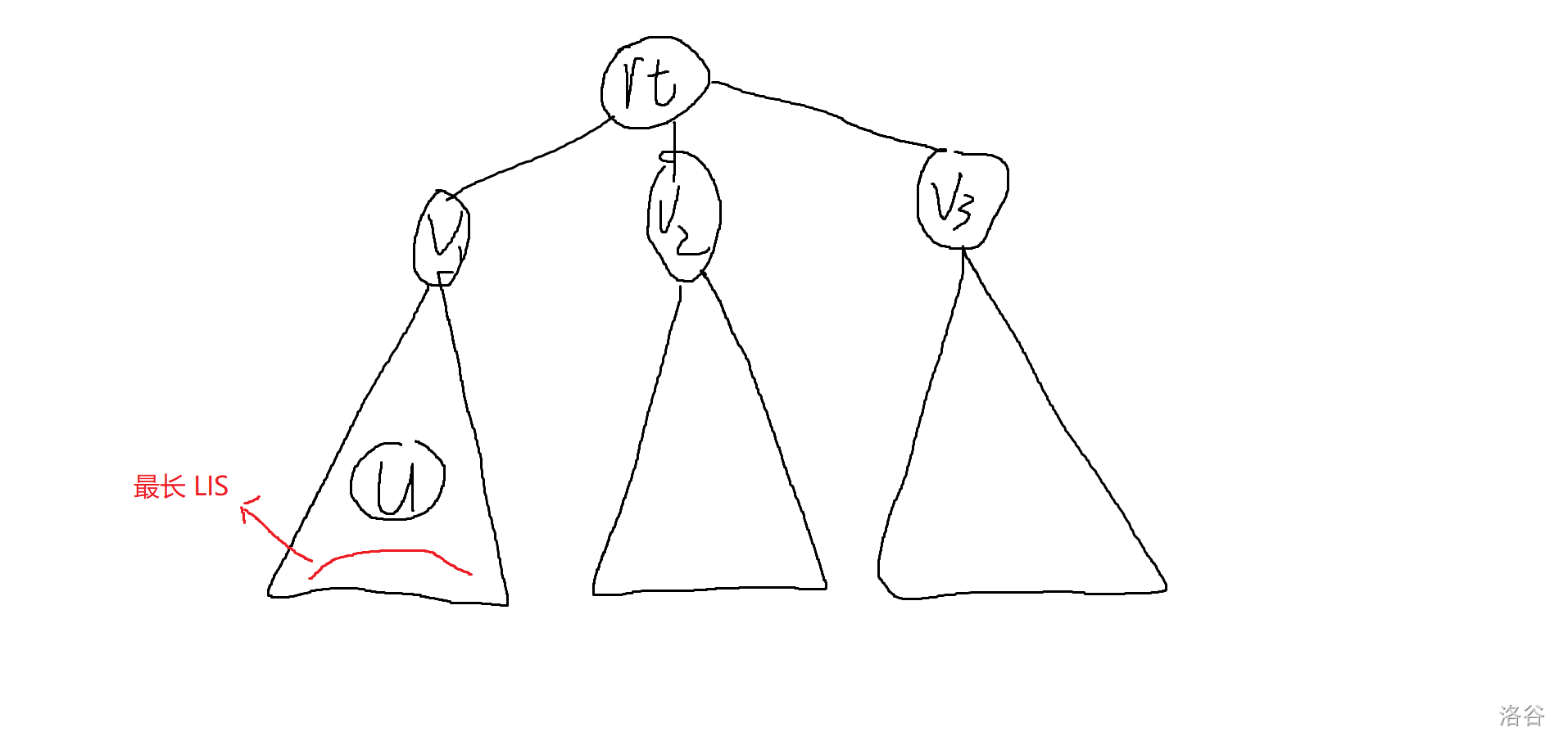
可能换根之后长这样:
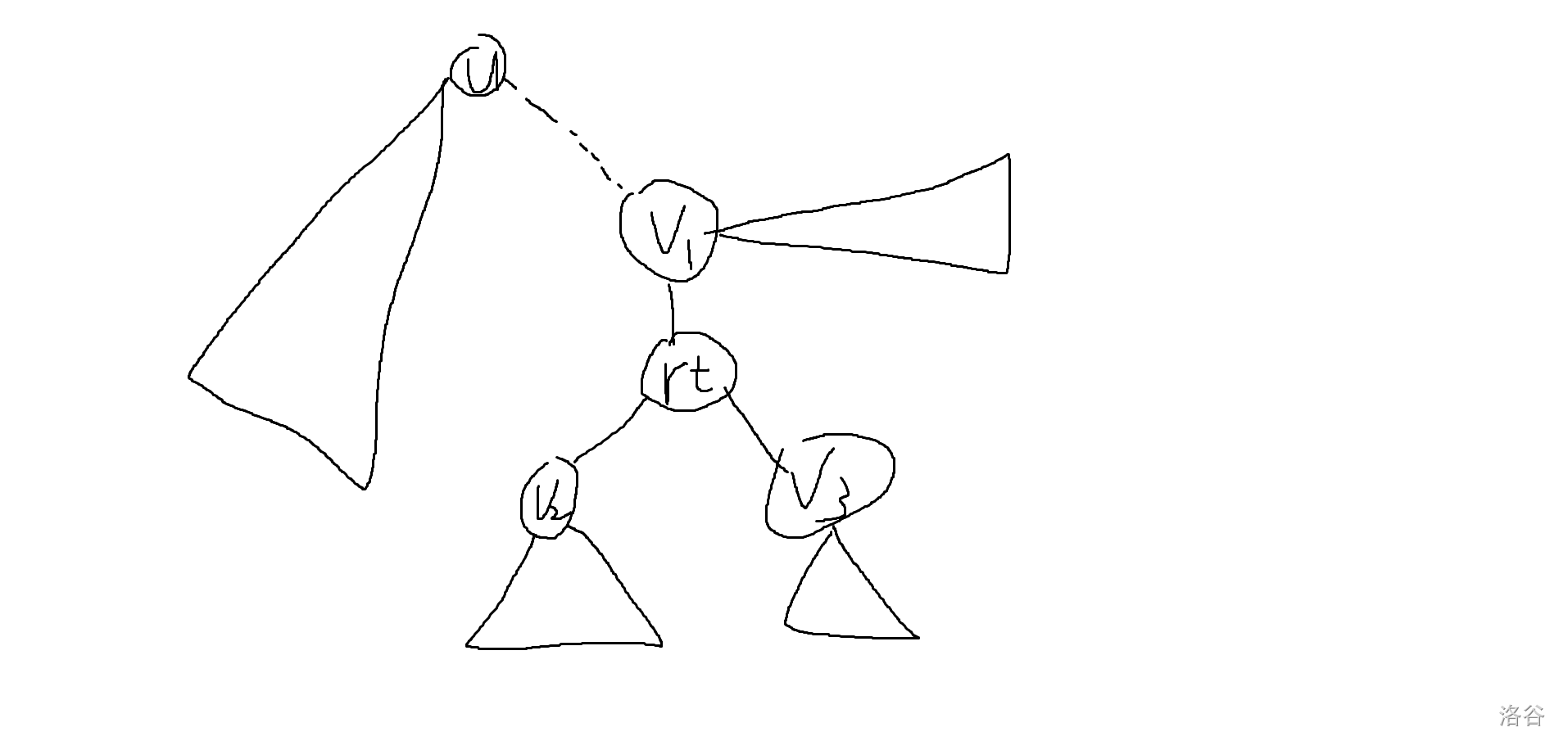
会发现其实我们没有必要重新算一遍子树 \(v2,v3\) 的答案,因为他们的形态并没有改变,之后也不会再改变,同理 \(rt\) 这棵子树之后的形态也不会变了,可以直接用 \(v2,v3\) 更新出他的信息。
所以我们在算以 \(u\) 为根的答案时,没有必要再去做 \(rt\) 这棵子树。
这样每一次要重新做的树的大小就是 \(n,\frac{n}{2},\frac{n}{4},…\),总复杂度就是 \(O(n\log n)\)。
解法三
如果我们能求出每个点子树内和子树外的最长 \(LIS\),那就可以快速求出删掉每个点之后的答案。
但很可惜,子树外的最长 \(LIS\) 并不好求。
换个角度考虑,我们刚才的思路是要使最长 LIS 变短就必须去他所在的子树里面删,但其实可以更进一步,容易证明我们要删的一定是最长 \(LIS\) 所在链上面的点。
那么我们需要子树外的最长 \(LIS\) 的那些点就只有这条链上的点的儿子或者父亲,而这些信息只需要分别以这条链的两端为根跑 dfs 就变成子树内的信息了。
所以只需要会求子树内的最长 \(LIS\) 即可。
因为笔者是懒虫,所以只实现了最好实现的解法一。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define ls(p) t[p].ls
#define rs(p) t[p].rs
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e5+5,inf=1e5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,a[N],tot,head[N],to[N<<1],Next[N<<1],Ans=N;
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
namespace Work{
PII operator + (const PII&x,const PII&y){return {max(x.fi,y.fi),max(x.se,y.se)};}
int rt[N],tot,ans[N];
struct node{
int ls,rs,f,g;
}t[N*20];
int New(){
++tot;
t[tot]={0,0,0,0};
return tot;
}
void pushup(int p){
t[p].f=max(t[ls(p)].f,t[rs(p)].f);
t[p].g=max(t[ls(p)].g,t[rs(p)].g);
}
void change(int &p,int L,int R,int x,int maxn1,int maxn2){
if(!p) p=New();
if(L==R){
t[p].f=max(t[p].f,maxn1);
t[p].g=max(t[p].g,maxn2);
return;
}
int mid=(L+R)>>1;
if(x<=mid) change(t[p].ls,L,mid,x,maxn1,maxn2);
else change(t[p].rs,mid+1,R,x,maxn1,maxn2);
pushup(p);
}
PII ask(int p,int L,int R,int l,int r){
if(!p||l>r) return {0,0};
if(l<=L&&R<=r) return {t[p].f,t[p].g};
int mid=(L+R)>>1;
if(r<=mid) return ask(t[p].ls,L,mid,l,r);
else if(l>mid) return ask(t[p].rs,mid+1,R,l,r);
else return ask(t[p].ls,L,mid,l,r)+ask(t[p].rs,mid+1,R,l,r);
}
int merge(int p,int q,int L,int R,int u){
if(!p||!q) return p+q;
if(L==R){
t[p].f=max(t[p].f,t[q].f);
t[p].g=max(t[p].g,t[q].g);
return p;
}
ans[u]=max({ans[u],t[ls(p)].f+t[rs(q)].g,t[ls(q)].f+t[rs(p)].g}); //统计经过 u 但是 u 不在 LIS 里的路径的贡献
int mid=(L+R)>>1;
t[p].ls=merge(t[p].ls,t[q].ls,L,mid,u);
t[p].rs=merge(t[p].rs,t[q].rs,mid+1,R,u);
pushup(p);
return p;
}
void dfs(int u,int fa){
ans[u]=1;
int maxn1=1,maxn2=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs(v,u);
ans[u]=max(ans[u],ans[v]);
int Up=ask(rt[v],1,inf,1,a[u]-1).fi,Down=ask(rt[v],1,inf,a[u]+1,inf).se;
maxn1=max(maxn1,Up+1);
maxn2=max(maxn2,Down+1);
ans[u]=max(ans[u],ask(rt[u],1,inf,1,a[u]-1).fi+1+Down);
ans[u]=max(ans[u],Up+1+ask(rt[u],1,inf,a[u]+1,inf).se);
rt[u]=merge(rt[u],rt[v],1,inf,u);
}
change(rt[u],1,inf,a[u],maxn1,maxn2);
ans[u]=max({ans[u],t[rt[u]].f,t[rt[u]].g});
}
int Main(int root){
tot=0;
for(int i=1;i<=n;i++) rt[i]=ans[i]=0;
dfs(root,0);
int son=0;
for(int i=head[root];i;i=Next[i]){
int v=to[i];
if(ans[v]>ans[son]) son=v;
}
Ans=min(Ans,ans[son]);
return son;
}
};
int Size[N],rt,num,maxn[N];
bool vis[N];
void dfs(int u,int fa,bool op){
Size[u]=1,maxn[u]=0;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa||vis[v]) continue;
dfs(v,u,op);
Size[u]+=Size[v];
if(op) maxn[u]=max(maxn[u],Size[v]);
}
if(op){
maxn[u]=max(maxn[u],num-Size[u]);
if(maxn[u]<maxn[rt]) rt=u;
}
}
void solve(int t){
vis[t]=true;
int u=Work::Main(t);
if(vis[u]) return;
rt=0;
maxn[rt]=num=Size[u];
dfs(u,0,1);
dfs(u,0,0);
solve(rt);
}
signed main(){
freopen("lis.in","r",stdin);
freopen("lis.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
rt=0;
maxn[rt]=num=n;
dfs(1,0,1);
dfs(rt,0,0);
solve(rt);
printf("%d\n",Ans);
return 0;
}
C.并行程序
题意
有 \(n\) 个程序,所有程序共享一个全局整形变量 \(x\),同时第 \(i\) 个程序有一个专属的私有计数器 \(y\),第 \(i\) 个程序由 \(l_i\) 个指令组成,每个指令都属于以下四种类型:
W:将全局变量 \(x\) 的值写入私有计数器 \(y\),即令 \(x\to y\)。Z:将私有计数器 \(y\) 的值写入全局变量 \(x\),即令 \(x\gets y\)。+ c:表示将私有计数器 \(y\) 的值加上正常数 \(c\)。- c:表示将私有计数器 \(y\) 的值减去正常数 \(c\)。
初始时 \(x\) 和所有 \(y\) 都是 \(0\)。
你需要指定某种顺序来执行这 \(n\) 个程序,具体的,记某一时刻第 \(i\) 个程序已经执行了 \(a_i\) 个指令,那么下一个时刻你需要选择一个 \(i\in [1,n],a_i<l_i\),并执行这个程序的第 \(a_i+1\) 个指令。
问所有程序都执行完毕后,\(x\) 的值最小可能是多少。
多测。
数据范围:\(1\le T,n,l_i \le 10^6,1\le c \le 10^9\),一个测试点中所有数据的 \(\sum l_i\) 之和不超过 \(10^6\)。
时限: \(9s\)。
题解
蒋凌宇的视频讲解
Day10 模拟赛
什么网格专场。
A.这是第一题
题意
一张 \(n\times m\) 的网格,下标从 \(1\) 开始,列之间是循环的,即 \(m+1\) 列其实是第 \(1\) 列,\(-1\) 列其实是第 \(m\) 列。(行是不循环的)
有些格子上有障碍(#),有些格子上有硬币 (B),其余格子都是空地(.),Alice 和 Bob 在上面博弈,轮流操作,Alice 先手,操作的人需要选择一个硬币,假设他的坐标是 \((i,j)\),并把这个硬币移到 \((i+1,j),(i,j+1),(i,j-1)\) 三个位置中的一个。需要保证每个硬币不能重复经过一个格子两次(不同的硬币之间互不影响,允许硬币重叠)。不能操作的人输。
请求出获胜者是谁。
数据范围:\(1\le n,m\le 10^3\)。
题解
题意等价于求出每个棋子的 SG 值。
设 \(F(x,y,[l,r])\) 表示目前在位置 \((x,y)\),第 \(x\) 行的 \([l,r]\) 已经被走过了(如果 \(l>r\) 意味着走过的是 \([l,m]\cup [1,r]\)),此时的 SG 值。容易发现除了 \(l=r\) 的情况必然有 \(y=l\)(即只能往左走) 或者 \(y=r\)(即只能往右走)。那么 \(SG(x,y)\) 就等于 \(mex(SG(x+1,y),F(x,y-1,[y-1,y]),F(x,y+1,[y,y+1]))\)。
以 \(y=l<r\) 为例。
虽然状态数还是有 \(O(nm^2)\),但是会发现 SG 值的值域很小,只有 \(0,1,2,3\) 四种情况,且 \(F(x,y,[y,r])\) 的值在知道 \(F(x,m,[m,r])\) 后就可以推出来了,那么可以设 \(G(x,y,c)\) 表示当 \(F(x,m,[m,r])=c\) 时 \(F(x,y,[y,r])\) 的值,\(G\) 可以 \(O(m)\) 递推。对于不合法情况 SG 值就设为 \(-1\)。
现在还需要知道每个 \(r\) 对应的 \(F(x,m,[m,r])\)。同样的,\(F(x,m,[m,r])\) 在知道 \(F(x,t,[t,r]),t\ge r\) 的值之后就可以推出来了。所以设 \(H(x,t,c)\) 表示当 \(F(x,t,[t,r])=c\) 时 \(F(x,m,[m,r])\) 的值,\(H\) 也可以 \(O(m)\) 递推。那么 \(F(x,m,[m,r])\) 就等于 \(H(x,r,-1)\)。
复杂度 \(O(nm)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define eb emplace_back
#define LEFT 1
#define RIGHT 0
using namespace std;
const int N=1e3+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,SG[N][N],f[N][N][3];;
char c[N][N];
bool stater[N];
bool flag[4];
bool check(int i,int j){ return c[i][j]!='#'; }
int mex(vector<int> vec){
flag[0]=flag[1]=flag[2]=flag[3]=0;
for(int x:vec) if(x<=3) flag[x]=true;
int ans=0;
while(flag[ans]) ans++;
return ans;
}
int mex2(int x,int y){
if(x!=0&&y!=0) return 0;
if(x!=1&&y!=1) return 1;
return 2;
}
int dfs(int i,int j,int op){
if(f[i][j][op]!=-1) return f[i][j][op];
vector<int> vec;
if(i<n&&check(i+1,j)) vec.eb(SG[i+1][j]);
if(op==2){
if(check(i,(j-1+m)%m)) vec.eb(dfs(i,(j-1+m)%m,LEFT));
if(check(i,(j+1)%m)) vec.eb(dfs(i,(j+1)%m,RIGHT));
}
else if(op==LEFT){
if(check(i,(j-1+m)%m)) vec.eb(dfs(i,(j-1+m)%m,LEFT));
}
else{
if(check(i,(j+1)%m)) vec.eb(dfs(i,(j+1)%m,RIGHT));
}
return f[i][j][op]=mex(vec);
}
int G[N][4],F[N],H[N][4],Left[N],Right[N];
void work(int x,int f[]){
for(int y=0;y<m;y++){
for(int c=0;c<=3;c++){
if(y==0) G[y][c]=mex2(c,SG[x+1][y]);
else if(y==m-1) G[y][c]=c;
else G[y][c]=mex2(G[y-1][c],SG[x+1][y]);
}
}
for(int t=m-1;t>=0;t--){
for(int c=0;c<=3;c++){
if(t==m-1) H[t][c]=c;
else H[t][c]=H[t+1][mex2(c,SG[x+1][t+1])];
}
}
for(int r=0;r<m;r++) F[r]=H[r][3];
for(int y=0;y<m;y++) f[y]=G[(y-1+m)%m][F[y]];
}
signed main(){
freopen("first.in","r",stdin);
freopen("first.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
cin>>c[i][j];
if(c[i][j]=='#') stater[i]=true;
f[i][j][0]=f[i][j][1]=f[i][j][2]=-1;
}
}
for(int j=0;j<m;j++) SG[n+1][j]=4;
int res=0;
for(int x=n;x>=1;x--){
if(m==1){
if(c[x][0]=='#') SG[x][0]=4;
else SG[x][0]=(SG[x+1][0]==0)?1:0;
}
else if(stater[x]){
for(int y=0;y<m;y++){
if(c[x][y]=='#') SG[x][y]=4;
else SG[x][y]=dfs(x,y,2);
}
}
else{
work(x,Left);
reverse(c[x],c[x]+m);
for(int i=0;i<m-1-i;i++) swap(SG[x+1][i],SG[x+1][m-1-i]);
work(x,Right);
reverse(Right,Right+m);
reverse(c[x],c[x]+m);
for(int i=0;i<m-1-i;i++) swap(SG[x+1][i],SG[x+1][m-1-i]);
for(int y=0;y<m;y++){
vector<int> vec;
vec.eb(Left[y]),vec.eb(Right[y]),vec.eb(SG[x+1][y]);
SG[x][y]=mex(vec);
}
}
for(int y=0;y<m;y++) if(c[x][y]=='B') res^=SG[x][y];
}
puts(res?"Alice":"Bob");
return 0;
}
B.这是第二题
题意
有一个 \(2n\times 2m\) 的网格,下标从 \(0\) 开始,初始网格的 \((i,j)\) 格子上的数是 \(2mi+j+1\)。并对网格按照 \(2\times 2\) 为单位进行交替黑白染色。
你需要维护下面五个操作:
- \(\forall 0\le j < m\),交换 \(2j,2j+1\) 这两列。
- \(\forall 0\le j<m-1\),交换 \(2j+1,2j+2\) 这两列。
- \(\forall 0\le i < n\),交换 \(2i,2i+1\) 这两行。
- \(\forall 0\le i<n-1\),交换 \(2i+1,2i+2\) 这两行。
- 对于每一个黑色 \(2\times 2\) 正方形,把里面的数按照顺时针旋转;对于每一个白色 \(2\times 2\) 正方形,把里面的数按照逆时针旋转。
现在给出一个长度为 \(Q\) 的操作序列,请输出最终的网格。
数据范围:\(1\le Q,nm\le 10^6\)。
题解
会发现 \(2,4\) 操作非常不友好,因为他们并不会操作到第一列(行)和最后一列(行)。
我们可以把原图不断地镜像对称,铺满整个平面,但注意此时依旧是交替进行黑白染色,不是复制原图的颜色,比如当 \(n=2,m=2\) 时镜像三次就如下图所示(黑框中的数就是染黑的):
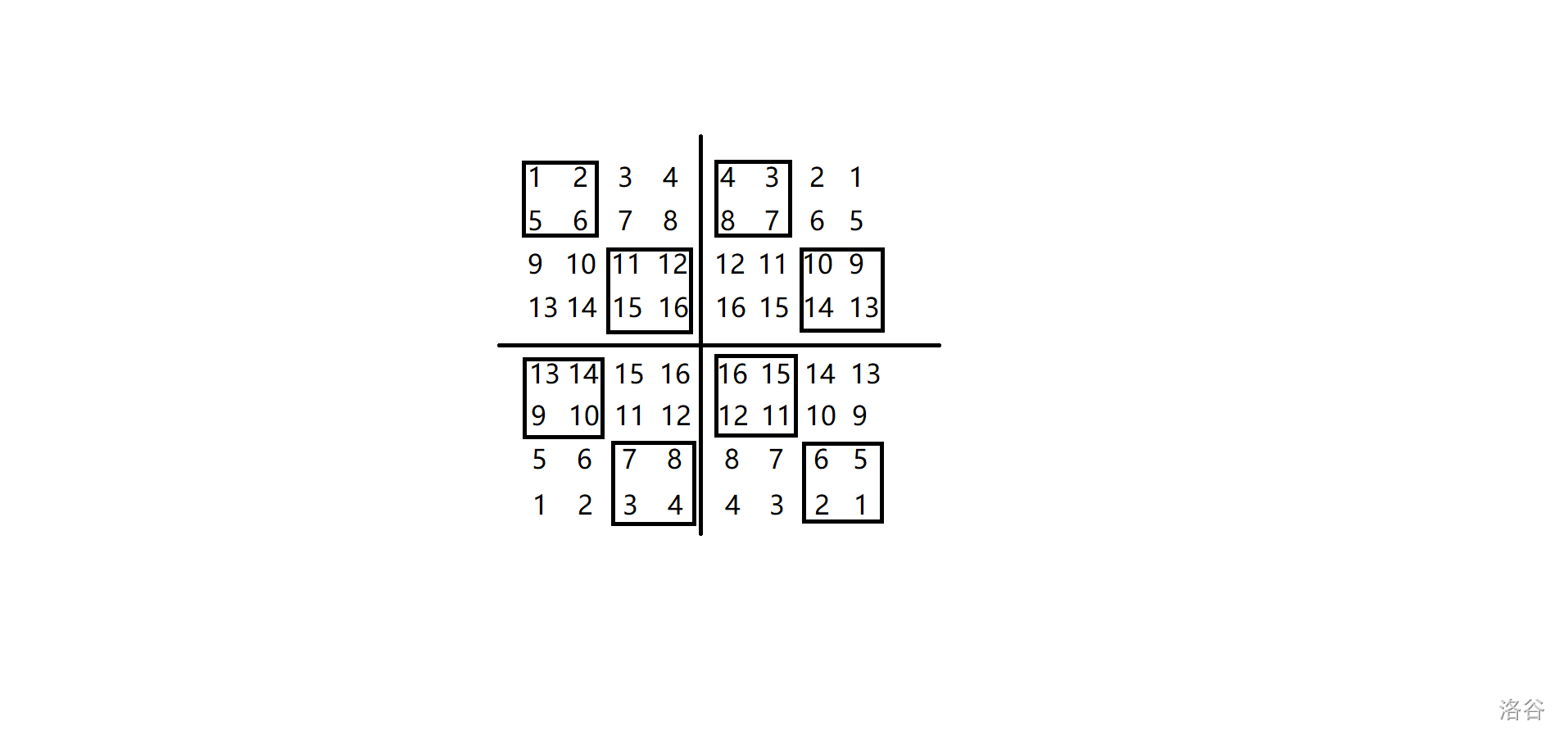
会发现此时相邻边界上的数是一模一样的,也就是说此时进行 \(2\) 操作可以认为是交换所有的 \(2j+1,2j+2\) 列(\(4\) 操作同理)。
并且不难验证此时 \(1,3,5\) 操作操作完同样可保证相邻边界上的数一样
所以此时一个点最终横纵坐标的平移量只跟他初始横纵坐标的奇偶性和颜色决定,因此只需要模拟 \(2\times 2\times 2\) 个点的轨迹即可。
最后再把每个点的坐标镜像回去就可以了。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
PII operator + (const PII&x,const PII&y){ return {x.fi+y.fi,x.se+y.se}; }
int n,m,Q,x[N];
bool staterA=true,staterC=true;
int Val(int i,int j){return 2*m*i+j+1;}
PII deta[2][2][2];
int calc(int val){
if(val>=0) return val/2;
else return (val-1)/2;
}
int calc1(int y){return (y%2==0)?1:(-1);}
int calc2(int y){return (y%2==0)?(-1):1;}
int calc3(int x){return (x%2==0)?1:(-1);}
int calc4(int x){return (x%2==0)?(-1):1;}
int get(int i,int j,int k,int x,int y){
bool flag=0;
if(calc(x+i)%2!=0) flag^=1;
if(calc(y+j)%2!=0) flag^=1;
return k^flag;
}
PII calc5(int x,int y,int c){
x=abs(x%2),y=abs(y%2);
if(c==0){ //Black
if(x==0&&y==0) return {0,1};
if(x==0&&y==1) return {1,0};
if(x==1&&y==1) return {0,-1};
if(x==1&&y==0) return {-1,0};
}
else{ //White
if(x==0&&y==0) return {1,0};
if(x==0&&y==1) return {0,-1};
if(x==1&&y==1) return {-1,0};
if(x==1&&y==0) return {0,1};
}
}
vector<vector<int> > a;
int Get(int x,int n){
int cnt=1+x/(2*n);
x=x%(2*n);
if(cnt&1) return x;
else return 2*n-1-x;
}
signed main(){
freopen("second.in","r",stdin);
freopen("second.out","w",stdout);
n=read(),m=read(),Q=read();
for(int i=0;i<=1;i++) for(int j=0;j<=1;j++) for(int k=0;k<=1;k++) deta[i][j][k]={0,0};
for(int _=1;_<=Q;_++){
x[_]=read();
for(int i=0;i<=1;i++){
for(int j=0;j<=1;j++){
for(int k=0;k<=1;k++){
if(x[_]==1) deta[i][j][k].se+=calc1(j+deta[i][j][k].se);
if(x[_]==2) deta[i][j][k].se+=calc2(j+deta[i][j][k].se);
if(x[_]==3) deta[i][j][k].fi+=calc3(i+deta[i][j][k].fi);
if(x[_]==4) deta[i][j][k].fi+=calc4(i+deta[i][j][k].fi);
if(x[_]==5) deta[i][j][k]=deta[i][j][k]+calc5(i+deta[i][j][k].fi,j+deta[i][j][k].se,get(i,j,k,deta[i][j][k].fi,deta[i][j][k].se));
}
}
}
}
a.resize(2*n);
for(int i=0;i<2*n;i++) a[i].resize(2*m);
for(int i=0;i<2*n;i++){
for(int j=0;j<2*m;j++){
int x=i+deta[i&1][j&1][(i/2%2+j/2%2)%2].fi,y=j+deta[i&1][j&1][(i/2%2+j/2%2)%2].se;
if(x<0) x=-x-1;
if(y<0) y=-y-1;
x=Get(x,n),y=Get(y,m);
a[x][y]=Val(i,j);
}
}
for(int i=0;i<2*n;i++){
for(int j=0;j<2*m;j++){
printf("%d ",a[i][j]);
}
puts("");
}
return 0;
}
C.这是第三题
题意
有一个大小为 \(n\times m\) 的网格,初始有一些格子上有棋子,现在你需要在一些空格子上再放上一些棋子,使得存在唯一的一种匹配棋子的方式。你需要输出最少新放的棋子数,或者报告无解。
一种匹配棋子的方式合法当且仅当每个棋子都在一组匹配中,且一组匹配中的两个棋子在同一行或者同一列。
数据范围:\(1\le n,m\le 10^3\)。
Day11 模拟赛
A.硬币
题意
这是一道交互题。
有 \(n\) 堆硬币,下标从 \(0\) 开始,第 \(i\) 堆硬币的硬币数量是 \(a_i\),有且仅有一堆硬币全是假币,其余都是真币。一枚真币的重量是 \(5\),一枚假币的重量是 \(6\)。
每次你可以向交互库询问一个长度为 \(n\) 的数组 \(p\) 满足 \(0\le p_i \le a_i\) 表示从第 \(i\) 堆硬币中取出 \(p_i\) 个硬币,最后交互库会返回从这 \(n\) 堆硬币中取出的所有硬币的重量和。
你需要求出假硬币是哪一个堆,并最小化询问次数。
数据范围: \(1\le n\le 10^6,1\le a_i\le 10^9\)。
题解
首先询问返回的结果等价于取出的硬币中假币的数量,换句话说,如果取出的假币的数量是 \(x\),那么假币只能在那些 \(p_i=x\) 的堆中。
所以每一次询问相当于把硬币分成若干个集合,然后可以知道假币具体在哪个集合中。
所以询问策略就是一棵树,有 \(n\) 个叶子,每个叶子代表一堆硬币,非叶结点的 \(p\) 值需要小于等于子树中所有叶子的 \(a\) 值。
容易发现如果一个集合中的数在排序后满足 \(a_i\ge i-1\),那么可以把他们的 \(p_i\) 依次设为 \(0,1,2,…\),因为 \(p_i\) 互不相同所以可以直接确定假币在哪一堆。否则无法一次询问直接找出假币。因此上面划分集合的时候需要满足这个限制。
所以可以得到答案的下界:\(\max_{x\ge 2}(\log_x (\sum_{y<x} cnt_y))\),其中 \(cnt_y\) 表示 \(a_i=y\) 的数量。
证明:显然对于每一个 \(x\),原问题比 \(\sum_{y<x} cnt_y\) 个 \(x-1\) 要难,而这个新问题的最优策略显然是 \(x\) 叉树(即每次选出来 \(x\) 个数放到一个集合,\(p_i\) 分别分配 \(0,1,2,…,x-1\)),此时答案是 \(\log_x(\sum_{y<x} cnt_y)\)。
要想达到这个下界可以直接贪心,从下往上构造这棵树,每次把点排序后从前往后考虑,如果他能放到当前的某个集合中就放,否则新开一个集合。最后把得到的每个集合当做上一层的节点,权值就设为集合中点权的最小值即可。
复杂度随便实现基本都是对的。
code
#include "coins.h"
#include<bits/stdc++.h>
#define fi first
#define se second
#define LL long long
#define PIV pair<int,vector<int> >
#define PII pair<int,int>
#define Debug puts("-----------------------------")
using namespace std;
const int N=1e6+5;
int n,a[N];
int solve(vector<PIV> vec){
if(vec.size()==1) return 0;
vector<int> b(vec.size());
for(int i=0;i<vec.size();i++) b[i]=i;
sort(b.begin(),b.end(),[&](int x,int y){return vec[x].fi<vec[y].fi;});
vector<PIV> node;
vector<vector<int> > ID;
int num=0;
set<PII> S;
for(int _=0;_<vec.size();_++){
PIV u=vec[b[_]];
int pos=0;
if(S.size()&&u.fi>=(*S.begin()).fi) pos=(*S.begin()).se,S.erase(S.begin());
else ++num,pos=num-1,node.resize(num),ID.resize(num),node[num-1].fi=INT_MAX;
node[pos].fi=min(node[pos].fi,u.fi);
ID[pos].emplace_back(b[_]);
S.insert({ID[pos].size(),pos});
for(int x:u.se) node[pos].se.emplace_back(x);
}
int number=solve(node);
vector<int> p(n);
LL sum=0;
for(int i=0;i<ID[number].size();i++){
int x=ID[number][i];
for(int y:vec[x].se) sum+=i,p[y]=i;
}
LL deta=weigh(p)-5*sum;
return ID[number][deta];
}
int solve(vector<int> A) {
n=A.size();
vector<pair<int,vector<int> > > all(n);
for(int i=0;i<n;i++) a[i]=A[i],all[i]={a[i],{i}};
return solve(all);
}
B.厵神
题意
有一个大小为 \(n\times m\) 的网格 \(a\),初始每个 \(a_{i,j}=1\)。
每一秒结束时,\(a_{i,j}\) 都会变成 \(a_{i,j-1}+a_{i,j+1}+a_{i-1,j}+a_{i+1,j}\)(越界的话就当做 \(0\))。
特殊的,在第 \(t\) 秒结束时,\(a_{x,y}\) 会变成 \(0\)。
现在请你求出在第 \(t’\) 秒结束时,\(a_{x’,y’}\) 对 \(1004535809\) 取模的值。
数据范围:\(2\le n\le 10^9,1\le m \le 10^9,1\le x,x’ \le n,1\le y,y’ \le m,1\le t \le 2\times 10^9,1\le t’ \le 10^5\)。
C.区间压缩
题意
太长了,直接上图。

数据范围: \(1\le n,q \le 5\times 10^5,1\le l_i\le r_i \le 10^6,1\le x_i\le y_i \le 10^6\)。
来源链接:https://www.cnblogs.com/FloatingLife/p/18838459











没有回复内容