cats 的 max

dp #子集合dp #状态压缩dp #状态压缩

题目

思路

本题只需要考虑\(k<m\)的情况，因为\(k\geq m\)时，每一列都必定可以选到其最大值，暴力即可算出答案

考虑到\(m\leq13\)，所以对每行进行状态压缩

\(mp[N][N]\)用来储存矩阵

\(a[i][mask]\)代表第\(i\)行中，\(mask(2)\)所对应列的元素之和

• 如\(mask:10010\)，则\(a[i][mask]=mp[i][1]+mp[i][4]\)
• \(mask\)中位置\(pos\)为1就代表第\(pos\)列的最大值取在\(mp[ i][pos]\)

如何预处理\(a[i][mask]\)呢？

• 如果对于每一行\(i\)所储存的\(2^m\)个\(mask\)进行遍历，把1的位置加进\(a[i][mask]\)中，时间复杂度将来到\(o(n·m·2^m)\)，\(TLE\)
• 因此需要采用前缀优化：通过\(lowbit\)将\(mask\)拆分为\(lowbit\ ,mask\wedge lowbit\)，通过递推\(a[i][mask]=a[i][lowbit]+a[i][mask \wedge lowbit]\)线性预处理出所有情况
• \(lowbit\leq mask\ ,mask\wedge lowbit<mask\)，而遍历\(mask\)时是从小到大遍历的，因此该递推即利用了之前处理好的前缀来优化复杂度

\(b[mask]\)代表所有\(a[i][mask]\ i\in[1,n]\)中的最大值

\(dp[cnt][mask]\)代表：现在选择了\(cnt\)行，这\(cnt\)行的状态或运算后为\(mask\)的权值最大值

状态转移：

• 遍历\(k\)次选择，对于一个\(mask\)，其子集记为\(mask2\)，则二者的补集为\(mask\wedge mask 2\)

\[dp[cnt][mask2]\times b[mask\wedge mask 2]=dp[cnt+1][mask] \]

• 当前选了\(cnt\)行，状态为\(mask 2\)，那么其与\(mask\wedge mask 2\)或运算后即可转移到\(mask\)状态，\(b[mask\wedge mask 2]\)就相当于选了新的一行，并且保证新的一行上的列最值与之前状态的列最值不会重叠（补集的作用）
• 一般dp由后往前写，所以修改一下即可：

\[dp[cnt][mask]=dp[cnt-1][mask2]\times b[mask\wedge mask 2] \]

• 枚举所有的\(mask\)及其子集的复杂度为\(3^m\)，所以总复杂度为\(o(m·3^m)\)
• 最后直接输出\(dp[k][one]\)即可

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const ll inf = 1e9 + 5;
#define int ll

const int N=1005,M=(1<<14);
int mp[N][N],a[N][M],dp[N][M],b[M];

void see2(int x){
    while(x){
        cout<<(x&1);
        x>>=1;
    }
}

void eachT() {
    int n,m,k;cin>>n>>m>>k;
    int one=(1<<m)-1;
    rep(tim,1,k){
        rep(mk,0,one)b[mk]=0,dp[tim][mk]=0;
    }
    rep(i,1,n){
        rep(j,1,m){
            cin>>mp[i][j];
            a[i][1<<(j-1)]=mp[i][j];          
        }
        rep(mk,0,one){
            int lb=mk&(-mk);
            a[i][mk]=a[i][mk-lb]+a[i][lb];
            b[mk]=max(b[mk],a[i][mk]);
        }
    }
    if(k>=m){      
        ll sum=0; 
        rep(j,1,m){
            int ma=0;
            rep(i,1,n)ma=max(ma,mp[i][j]);
            sum+=ma;
        }    
        cout<<sum<<'\n';
        return; 
    }

    rep(tim,1,k){
        rep(mk,0,one){
            for(ll s=mk;s;s=(s-1)&mk){
                int mk2=s;
                dp[tim][mk]=max(dp[tim][mk],dp[tim-1][mk2]+b[mk^mk2]);
            }
            dp[tim][mk]=max(dp[tim][mk],b[mk]);
        }
    }
    cout<<dp[k][one]<<'\n';
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) { 
        eachT(); 
    }
}

---

传送排序

线段树 #dp #线性dp

题目

思路

状态含义：

• \(dp[a_{i}]\)表示遍历到\(a_{i}\)时，将\(a_{i}\)排序，最多可以省下多少花费
• 每

状态转移：

\[dp[a_{i}]=max\{ dp[a_{i}-1]+1,max\{ dp[a_{j}] \}[a_{j}<a_{i}] \} \]

• 如果\(a_{i}-1\)已经出现过了，那么可以不需要建造传送门就排好序，此时节省了1的费用
• 用\(vis[N]\)数组维护每个数字是否出现过的信息
• 如果要建新的传送门到之前的点\(a_{j}[a_{j}<a_{i}]\)，那么没有节省任何费用；为了使最后剩下的花费最多，所以尽可能转移到节省花费较大的状态上，即取max
• 在遍历过程中若\(a_{i}\)为1，那么节省的花费必然为1，因为他不用建传送门
• 取\(ans=n\)代表所有的数字都建传送门所需要的花费，那么\(ans-max\{ dp[i] \}[1\leq i\leq n]+1\)便是最少的花费
• 对于\(a_{n}\)需要特别讨论：如果\(max\{ dp[i] \}\)取得最大值时的\(i\)为\(n\)，那么便在刚刚答案的基础上-1，因为数字\(n\)不需要在其右边建传送门

最后用一棵线段树维护区间最大值即可

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<map>
#include<iomanip>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define mid ((l+r)>>1)
const int N=2e5+5;
int n,rt,ls[N<<2],rs[N<<2],ma[N<<2],node,dp[N];
bool vis[N];

void pushup(int p){
    ma[p]=max(ma[ls[p]],ma[rs[p]]);
}

void update(int&p,int l,int r,int pos,int val){
    if(!p)p=++node;
    if(l==r){ma[p]=val;return;}
    if(pos<=mid)update(ls[p],l,mid,pos,val);
    else update(rs[p],mid+1,r,pos,val);
    pushup(p);
}

int query(int p,int l,int r,int x,int y){
    if(!p)p=++node;
    if(x<=l&&r<=y){return ma[p];}
    int res=0;
    if(x<=mid)res=max(res,query(ls[p],l,mid,x,y));
    if(y>mid)res=max(res,query(rs[p],mid+1,r,x,y));
    return res;
}

void eachT(){
    cin>>n;
    rt=node=0;
    rep(i,1,n)dp[i]=vis[i]=0;
    rep(i,1,(n<<2)){
        ls[i]=rs[i]=ma[i]=0;
    }
    int del=1,maxid=1;

    rep(i,1,n){
        int x;cin>>x;
        if(x==1){dp[x]=1;update(rt,1,n,1,1);vis[x]=1;continue;}
        dp[x]=query(rt,1,n,1,x-1);
        if(vis[x-1])dp[x]=max(dp[x-1]+1,dp[x]);
        vis[x]=1;
        update(rt,1,n,x,dp[x]);
        if(dp[x]>del||(dp[x]==del&&x>maxid)){
            del=dp[x];
            maxid=x;
        }   
    }
    cout<<n-del+(maxid!=n)<<'\n';
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)eachT();
}

---

取模

数学 #枚举

题目

思路

由于需要将所有的\(k\)输出，因此\(k\)的数量必然不会太大，考虑枚举\(k\)判断合法性

若将可重集进行去重，那么这个集合就是\(k\)的剩余系的子集
\(c\)代表数组\(a\%k\)的不同数量，因此必然有\(c\leq k\)

\(k\)可以将\(m\)分为\(\lfloor \frac{m}{k} \rfloor+1\)类数，即\(\left\lfloor \frac{a}{k} \right\rfloor=i,i=0,1,2,\dots\)

考虑每一类数，如第一类数：\(1,2,\dots,k-1\)，其中\(a\)数组中属于第一类的数的种类必然小于\(c\)，由此可以推广得\(a\)数组中属于每一类的数的种类必然小于\(c\)

设\(cnt\)为数组\(a\)中不同数字的数量，那么有：

\[cnt\leq \left( \left\lfloor \frac{m}{k} \right\rfloor +1 \right)\times c \]

不等式变形：

\[\begin{align} &cnt\leq \left( \left\lfloor \frac{m}{k} \right\rfloor +1 \right)\times c\\ \\ & \frac{cnt}{c}-1\leq \left\lfloor \frac{m}{k} \right\rfloor \leq \frac{m}{k}\\ \\ &k\leq \frac{m}{\frac{cnt}{c}-1} \end{align} \]

经过一系列的试错，发现需要将上界稍微缩至以下不等式才能通过：

\[k\leq \left\lfloor \frac{m}{\left\lceil \frac{cnt}{c} \right\rceil -1} \right\rfloor \]

最后需要特判\(cnt\leq c\)的情况，如果集合合法，那么\(k\)可以取任意数

代码实现

#include<iostream>
#include<vector>
#include<unordered_map>
#include<cmath>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;

const int N=5e5+5;

void eachT() {
    int n,m,c;cin>>n>>m>>c;
    unordered_map<int,int>mp;
    rep(i,1,n){
        int x;cin>>x;
        mp[x],mp[x]++;
    }
    int cnt=mp.size();
    if(cnt<=c){
        for(auto&ele:mp){
            if(ele.second!=n/c){
                cout<<0<<'\n';return;
            }
        }
        cout<<-1<<'\n';return;
    }
    set<int>ans;
    int up=m/((int)ceil(1.0*cnt/c)-1);
    rep(k,c,up){
        unordered_map<int,int>mod;
        for(auto&ele:mp){
            int num=ele.first,cnt=ele.second;
            mod[num%k]+=cnt;
        }
        if(mod.size()!=c)continue;
        bool flag=1;
        for(auto&ele:mod){
            int cnt=ele.second;
            if(cnt!=n/c){
                flag=0;break;
            }
        }
        if(!flag)continue;
        ans.insert(k);
    }
    cout<<ans.size()<<" ";
    for(auto&ele:ans)cout<<ele<<" ";
    cout<<'\n';
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) {
        eachT();
    }
}

---

钥匙迷宫

BFS #倍增 #dfs #树上差分 #差分 #染色

题目

思路

将门看作断边，门与门之间的点形成一个个连通块

首先很容易想到，如果一个点可以成功走完整个图，那么他所在的连通块必定也能走完整个图

接下来需要一个观察：

• 假如连通块\(A,B\)都可以走完整个图，以\(A\)内的点为起点模拟过程
• 设\(A\xrightarrow{door}B\)中间有门\(door\)阻挡，其钥匙\(key\)在\(A\)内
• 那么从\(A\)内取走钥匙，打开门，进入\(B\)是可以的
• 但是你会发现从\(B\)内无论如何都走不到\(A\)，因为\(key\)在\(A\)内
• 因此最开始的结论不成立，得到结论：能够走完整个图的连通块只有一个

接下来的问题变为如何找到这个连通块：

如果遍历所有的连通块，每个连通块都尝试是否能够走完整个图，那么复杂度来到\(o(n^2)\)，必然会超时

观察下图左侧的位置情况：

• 红色区域代表有可能拿到当前\(key\)随后走到\(door\)的区域
• 蓝色区域代表不可能拿到\(key\)的区域
  那么能够走完整个图的连通块必然在所有\(key-door\)的红色区域的交集中！
  

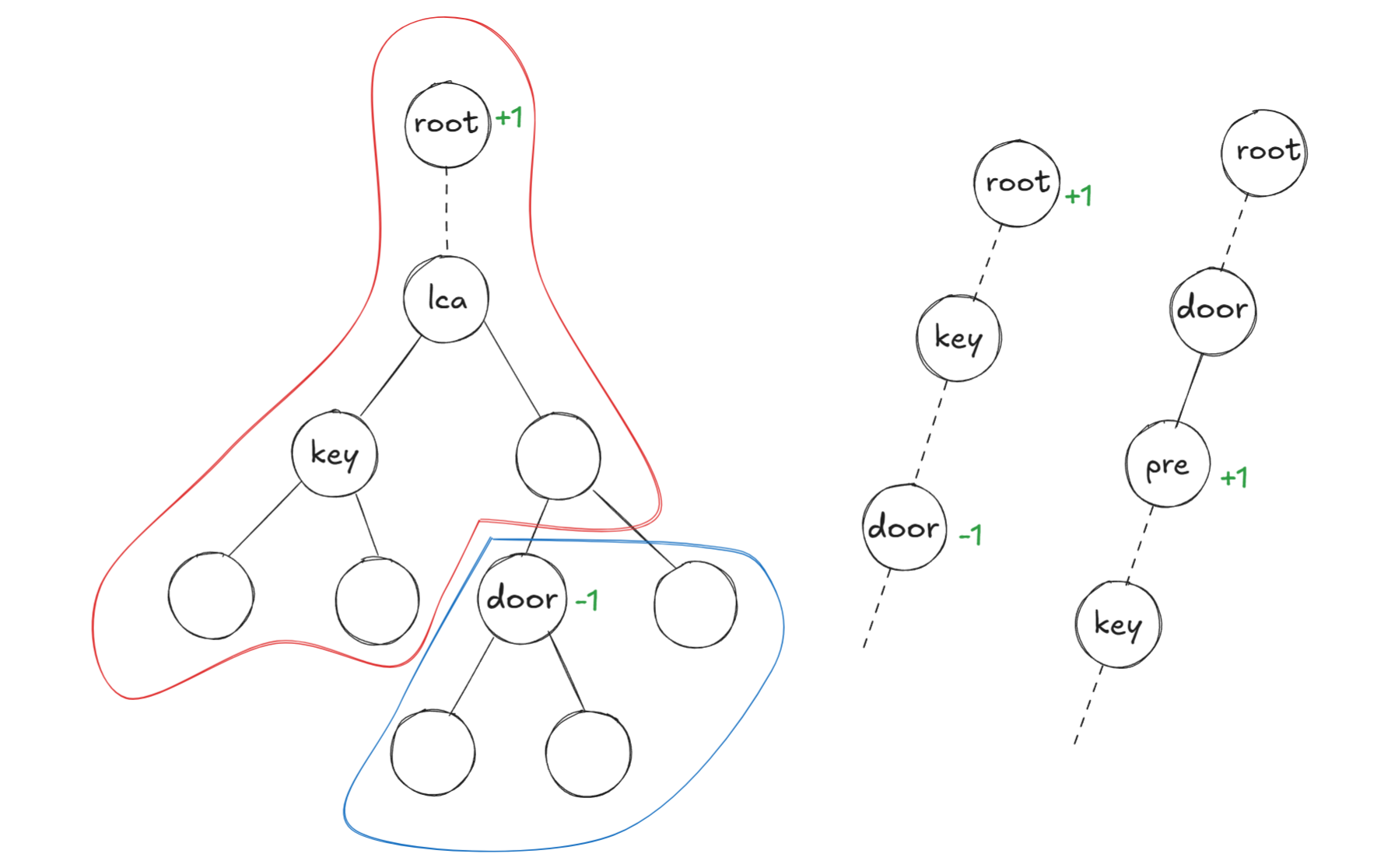
因此考虑通过树上差分进行染色：
需要计算的值\(sum\)代表每个点有多少个红色区域覆盖，当\(sum=n\)时就代表这个点在交集中

• 情况一：\(key,door\)存在\(lca\)
  • 此时在\(root\)位置\(+1\)，\(door\)位置\(-1\)即可
• 情况二：\(key\)在\(door\)的上方
  • 此时在\(root\)位置\(+1\)，\(door\)位置\(-1\)即可
• 情况三：\(door\)在\(key\)的上方
  • 此时需要通过树上倍增找到\(door\)的上一个节点\(pre\)，该位置\(+1\)

跑一遍DFS将差分还原为\(sum\)值，遍历所有节点将\(sum=n\)的点存入\(p[N]\)中便于后续输出答案

由于交集仅仅为合法的必要条件，因此还需要最后暴力判断合法性

随便在\(p\)中选取一个点作为起点\(start\)，跑一遍BFS判断当前连通块的合法性：
BFS伪代码：

• 取出队头的点\(u\)
• 遍历其未访问过的邻接节点\(v\)
• 如果\(v\)为一个门节点
  • 如果这个门是第一次访问
    • 如果对应的钥匙已经拿到了，那么\(v\)可以入队，标记为已访问；
    • 否则该门进入等待状态
  • 否则该门处于等待状态，不操作
• 否则\(v\)为一个钥匙节点
  • \(v\)入队，标记已访问
  • 如果当前钥匙所对应的门处于等待状态，那么门所对应的节点可以入队，标记状态

最后遍历\(vis\)数组判断是否所有点是否在BFS过程中已经抵达过，输出答案即可

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<unordered_set>
#include<string.h>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define mid ((l+r)>>1)

const int N=4e5+5;
int n;

struct node{
    vector<int>e;
    int cha,sum,val,tag;
}a[N];

struct kd{
    int key,door;
}mp[N];

vector<int>dep;
vector<vector<int>>F;
void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    F[u][0]=fa;
    rep(i,1,19)F[u][i]=F[F[u][i-1]][i-1];
    for(auto&son:a[u].e)if(son!=fa)dfs(son,u);
}

int lca(int u,int v){
    if(dep[u]<dep[v])swap(u,v);
    per(i,19,0)if(dep[F[u][i]]>=dep[v])u=F[u][i];
    if(u==v)return u;
    per(i,19,0)if(F[u][i]!=F[v][i])u=F[u][i],v=F[v][i];
    return F[u][0];
}

int find_pre(int st,int ed){
    per(i,19,0){
        if(dep[F[st][i]]>dep[ed])st=F[st][i];
        if(dep[st]==dep[ed]+1)return st;
    }
    return st;
}

void dfs2(int u,int fa,int val){
    a[u].sum=val+a[u].cha;
    for(auto&son:a[u].e){
        if(son==fa)continue;
        dfs2(son,u,a[u].sum);
    }
}

void eachT(){
    cin>>n;
    F.assign(2*n+1,vector<int>(21,0));dep.assign(2*n+1,0);
    rep(i,1,2*n){
        a[i].e.clear();
        a[i].cha=a[i].sum=0;
        int x;cin>>x;
        if(x>0){
            mp[x].key=i;a[i].tag=0;a[i].val=x;
        }else{
            mp[-x].door=i;a[i].tag=-1;a[i].val=-x;
        }
    }
    rep(i,1,2*n-1){
        int u,v;cin>>u>>v;
        a[u].e.push_back(v);
        a[v].e.push_back(u);
    }
    dfs(1,0);
    rep(i,1,n){
        int key=mp[i].key,door=mp[i].door;
        int l=lca(key,door);
        if(l!=key&&l!=door)a[1].cha++,a[door].cha--;
        if(l==door){
            a[find_pre(key,door)].cha++;
        }
        if(l==key)a[1].cha++,a[door].cha--; 
    }
    dfs2(1,0,0);
    vector<int>p;
    p.reserve(2*n);
    rep(i,1,2*n){
        if(a[i].tag!=-1&&a[i].sum==n){
            p.push_back(i);
        }
    }
    if(p.empty()){
        rep(i,1,n)cout<<0;
        cout<<'\n';
        return;
    }
    vector<bool>ans(n+1, 0);
    int st=p[0];
    queue<int> q;
    unordered_map<int,int>vis,wait;
    q.push(st);vis[st]=1;
    while(!q.empty()){
        int u=q.front();q.pop();
        for(auto v:a[u].e){
            if(vis[v])continue;
            if(a[v].tag==-1){
                if(!wait[v]){
                    int key=mp[a[v].val].key;
                    if(vis[key])q.push(v),vis[v]=1;
                    else wait[v]=1;
                }
            }else{
                q.push(v),vis[v]=1;
                int door=mp[a[v].val].door;
                if(wait[door])q.push(door),vis[door]=1;
            }
        }
    }
    int cnt=0;
    rep(i,1,2*n)if(vis[i]>0)cnt++;
    if(cnt==2*n){
        for(auto&u:p)ans[a[u].val]=1;
    }   
    rep(i,1,n) cout << ans[i];
    cout << '\n';
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)eachT();
}

来源链接：https://www.cnblogs.com/CUC-MenG/p/19027720