[IOI 2020] Stations 题解

23天前发布

UOJ （洛谷的通信题评测炸了）

题意描述

简化一下两个函数的意思。
label 函数就是给定你一棵无根树，你可以将原来的点的编号（\(i \in [0,n-1]\)）一一映射到一个新的区间（\(i \in [0, k]\)，其中 \(n – 1 \leq k\)），返回后来的编号。

find_next_station 函数就是查询，每次给定你重新编号过后的基准点和目标点，并给出基准点的相邻节点，你需要寻找一个离目标点最近的节点，并返回它。

思路

这道题有一个特别特殊的两个描述，一个是程序将会将所有 label 函数执行完后，再执行 find_next_station 函数，第二个是给出的相邻节点是将它的编号从小到大排序后返回的。

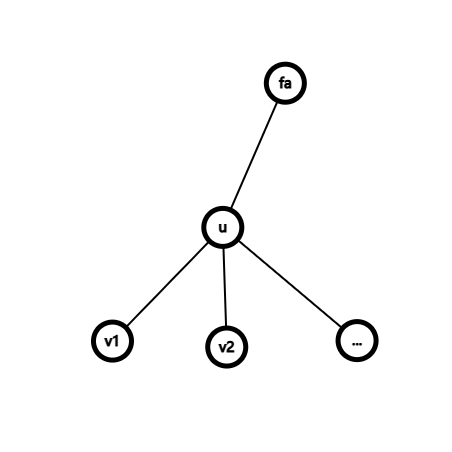
这道题乍一看像是 DFS序 的题目。现在我们设基准点为 \(u\)。可是我们无法判定目标点是在 \(u\) 的最后一个儿子上还是在 \(u\) 的父亲节点的其他儿子上，更或者在 \(u\) 的祖宗上。

考虑将 DFS 序转化成一个区间。

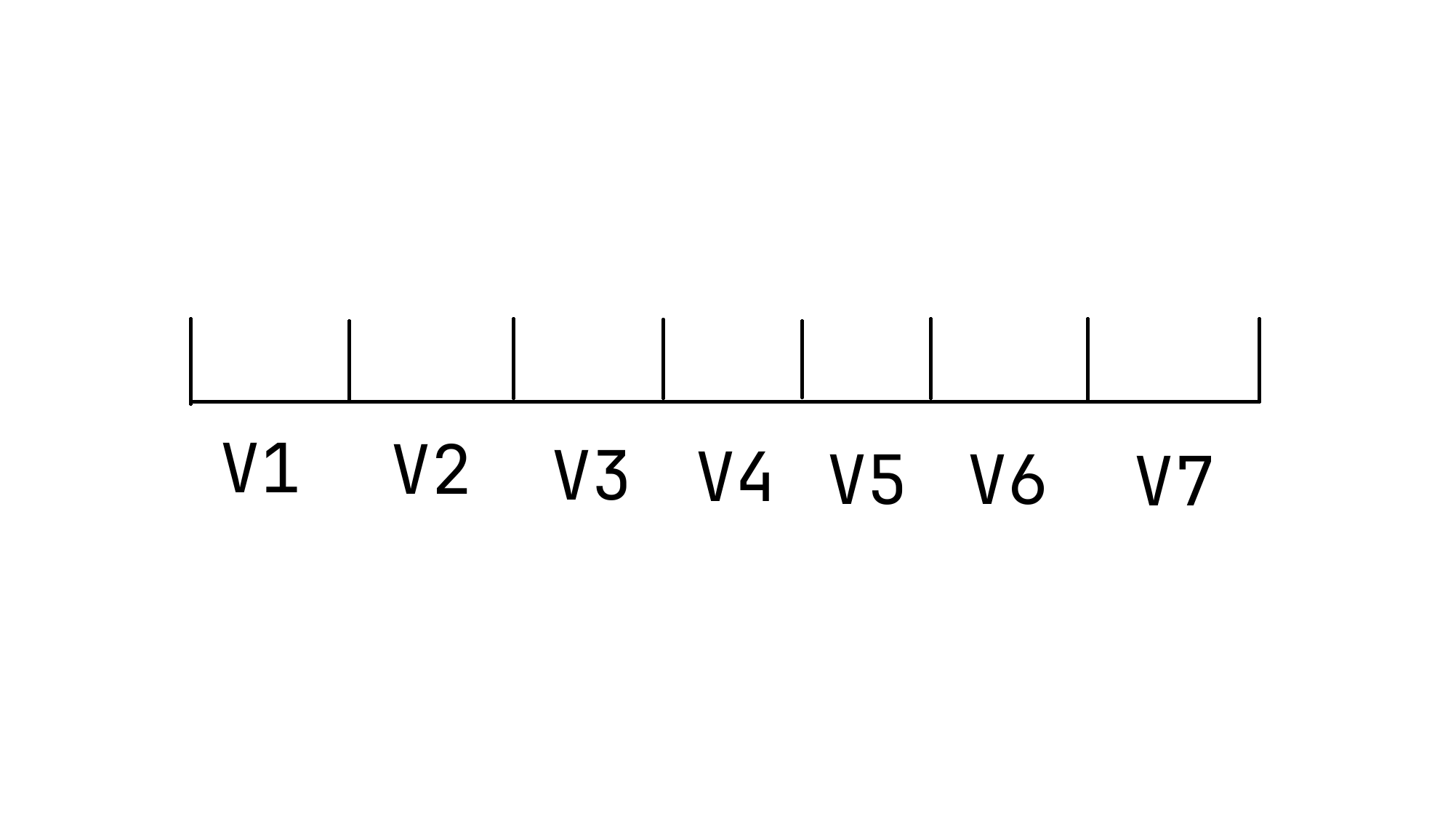
同上图，现在我们在 \(v\) 这一层全部记录入栈序，即左端点，可以看出，最后一个儿子的右端点没有记录。

于是我们可以在 \(u\) 这个节点记录出栈序，就可以解决了。

反之，如果在 \(v\) 这一层记录出栈序，那么 \(u\) 这一层只需要记录入栈序即可。

综上，分奇偶层决定记录入栈序或者是出栈序即可。

代码

#include <bits/stdc++.h>
#include "stations.h"
#define FASTIO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1005;
vector<int> adj[N];
int tag[N], ncnt, father[N], dep[N];
void build(int root, int fa, int depth) {
	dep[root] = depth;
	if (depth & 1) {
		for (auto son : adj[root]) {
			if (son == fa) continue;
			build(son, root, depth + 1);
		}
		tag[root] = ++ncnt;
	}
	else {
		tag[root] = ++ncnt;
		for (auto son : adj[root]) {
			if (son == fa) continue;
			build(son, root, depth + 1);
		}
	}
}
vector<int> label(int n, int k, vector<int> u, vector<int> v) {
	memset(tag, 0, sizeof tag);
	ncnt = -1;
	for (int i = 0; i < N; ++i)
		adj[i].clear();
	for (int i = 1; i < n; ++i) {
		adj[u[i - 1] + 1].push_back(v[i - 1] + 1);
		adj[v[i - 1] + 1].push_back(u[i - 1] + 1);
	}
	build(1, 0, 0);
	vector<int> res;
	for (int i = 1; i <= n; ++i) {
		res.push_back(tag[i]);
	}
	return res;
}
int find_next_station(int s, int t, vector<int> c) {
	if (c.size() == 1) return c[0];
	if (s <= c.back()) {
		if (t > s && t <= c[0]) 
			return c[0];
		for (int i = 1; i + 1 < int(c.size()); ++i) {
			if (t > c[i - 1] && t <= c[i]) return c[i];
		}
		return c.back();
	}
	else {
		for (int i = 1; i + 1 < int(c.size()); ++i) {
			if (t >= c[i] && t < c[i + 1]) return c[i];
		}
		if (t >= c.back() && t < s) return c.back();
		return c[0];
	}
}