【LeetCode 230】算法：二叉搜索树中第 K 小的元素

junjunyi

13天前发布

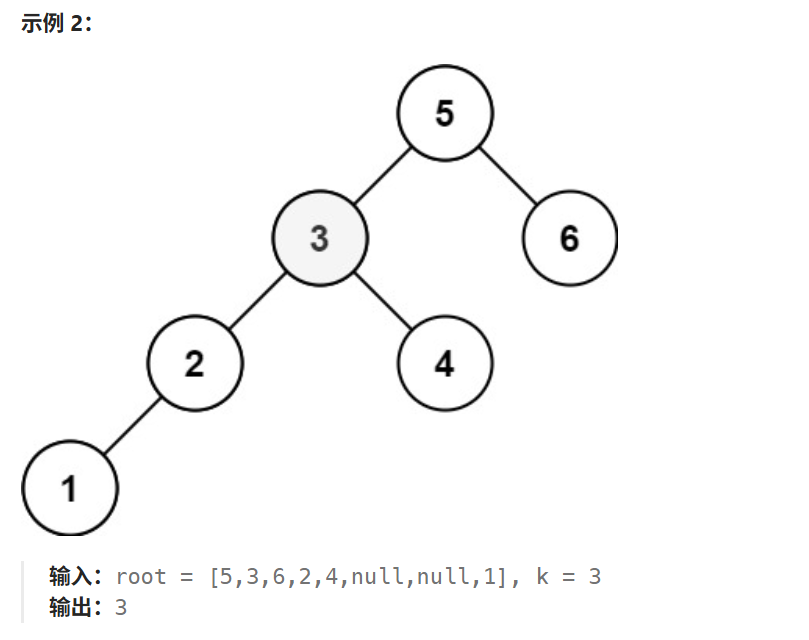
题目：给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

算法设计：

在二叉搜索树（BST）中，中序遍历可以按照从小到大的顺序访问所有节点。因此，要找到第 k 小的元素，可以通过中序遍历来实现。

中序遍历法：

使用递归或栈实现中序遍历。
在遍历过程中，记录已经访问的节点数量。
当访问到第 k 个节点时，返回该节点的值。

优化方案：

如果需要多次查询第 k 小的元素，可以使用一个数组来存储中序遍历的结果，然后直接通过索引访问。这样可以将多次查询的时间复杂度降低到 O(1)。

一、递归法

复杂度：

时间复杂度：O(n)，其中 n 是树中节点的数量。最坏情况下需要遍历所有节点。
空间复杂度：O(h)，其中 h 是树的高度。这是因为递归调用栈的深度最多为树的高度。

Java 代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    int count = 0;  // 记录当前访问的节点数量
    int res;        // 存储第 k 小的元素

    public int kthSmallest(TreeNode root, int k) {
        if(root==null)  return -1;
        // 中序遍历
        inOrderTraversal(root, k); 
        return res;
    }

    private void inOrderTraversal(TreeNode node, int k){
        // 递归出口
        if(node == null)  return;
        // 1.遍历左子树
        inOrderTraversal(node.left, k);
        // 2.先遍历完左子树，再访问当前结点
        count++;
        if(count == k){
            res = node.val;
            return;
        }
        // 3.遍历右子树
        inOrderTraversal(node.right, k);
    }
}

二、迭代法

复杂度：

时间复杂度：O(n)，因为每个节点最多被访问两次（一次入栈，一次出栈）。
空间复杂度：O(h)，因为栈的深度最多为树的高度 h。

Java 代码实现：

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode current = root;

        while (current != null || !stack.isEmpty()) {
            // 先将左子树的所有节点压入栈
            while (current != null) {
                stack.push(current);
                current = current.left;
            }
            // 访问栈顶节点
            current = stack.pop();
            k--;
            if (k == 0) {
                return current.val;
            }
            // 转向右子树
            current = current.right;
        }
        return -1; // 如果没有找到，返回一个错误值
    }
}

来源链接：https://www.cnblogs.com/Junjunyi/p/19029712

评分

欢迎为Ta评分