【LeetCode 199】力扣算法：二叉树的右视图

junjunyi

10天前发布

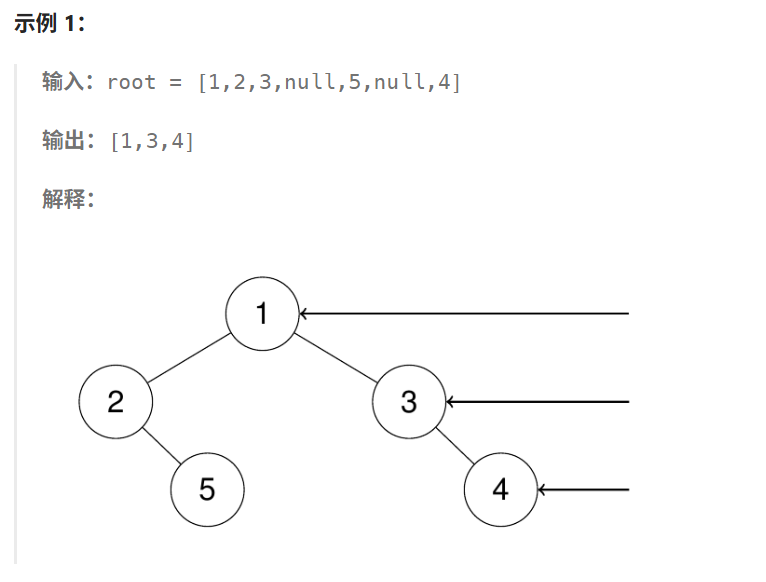
题目：给定一个二叉树的根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

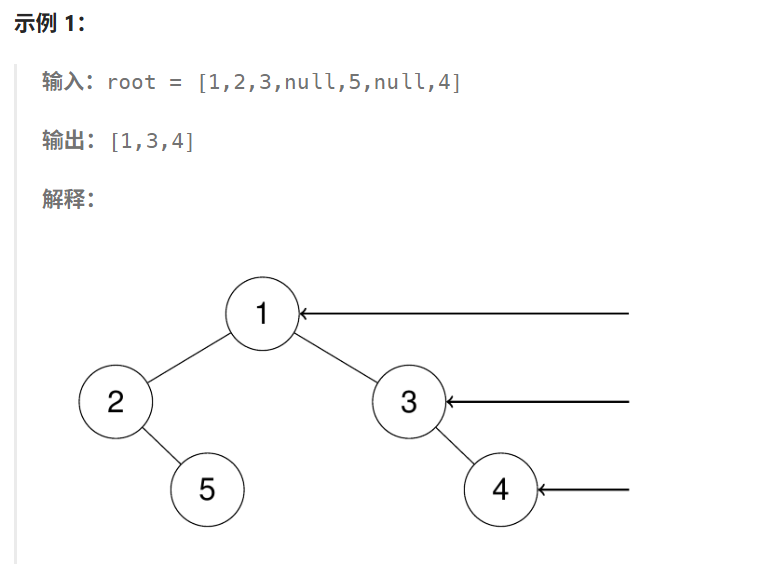
这个问题可以通过层次遍历（广度优先搜索，BFS）来解决。

核心思路：

使用一个队列来存储每一层的节点。
每次从队列中取出一层的节点，记录下这一层的最后一个节点的值（即从右侧能看到的节点）。
将当前层的节点的子节点（先左后右）加入队列。
重复上述过程，直到队列为空。

时间复杂度分析：

层次遍历：每个节点的操作（访问、加入队列、移除队列）的时间复杂度是 O(1)。由于每个节点都被访问一次，总的时间复杂度是 O(n)，其中 n 是二叉树中节点的总数。
队列操作：每次从队列中取出一个节点并处理其子节点，这些操作的时间复杂度是 O(1)。在每一层中，我们处理了所有节点，因此每一层的操作时间复杂度是 O(当前层的节点数)。由于所有层的节点总数是 n，因此总的时间复杂度仍然是 O(n)。

空间复杂度分析：

队列空间：队列在最坏情况下会存储所有节点，这发生在二叉树完全平衡时。在这种情况下，队列的最大长度是二叉树的宽度，即最后一层的节点数。队列的空间复杂度可以表示为 O(n)。
结果列表空间：结果列表存储了每一层的最后一个节点的值，因此其大小等于二叉树的高度 h。因此，结果列表的空间复杂度是 O(logn)。

时间复杂度：O(n)，因为每个节点被访问一次。

空间复杂度：O(n)，主要由队列的空间复杂度决定，结果列表的空间复杂度是 O(logn)，但队列的空间复杂度占主导。

Java 代码实现：

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        if(root==null){
            return new ArrayList<>();
        }
        List<Integer> res = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        
        // 先加入头节点，表示第一层
        queue.offer(root);
        // 遍历每层，取出该层的最后一个节点
        while(!queue.isEmpty()){
            int levelSize = queue.size();  //当前层的节点数量
            for(int i=1; i<=levelSize; i++){
                // 1.依次从队列取出节点
                TreeNode node = queue.poll(); 
                // 2.如果是当前层的最后一个节点，加入结果列表
                if(i == levelSize){
                    res.add(node.val);
                }
                // 3.把当前节点的子节点加入队列，先左后右
                if(node.left != null){
                    queue.offer(node.left);
                }
                if(node.right != null){
                    queue.offer(node.right);
                }
            }
        }

        return res;
    }
}

来源链接：https://www.cnblogs.com/Junjunyi/p/19036945

评分

欢迎为Ta评分