【LeetCode 114】算法进阶：二叉树展开为链表

junjunyi

10天前发布

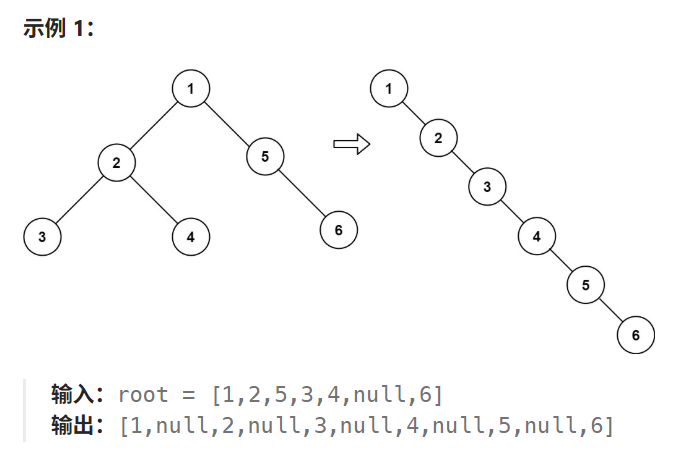
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

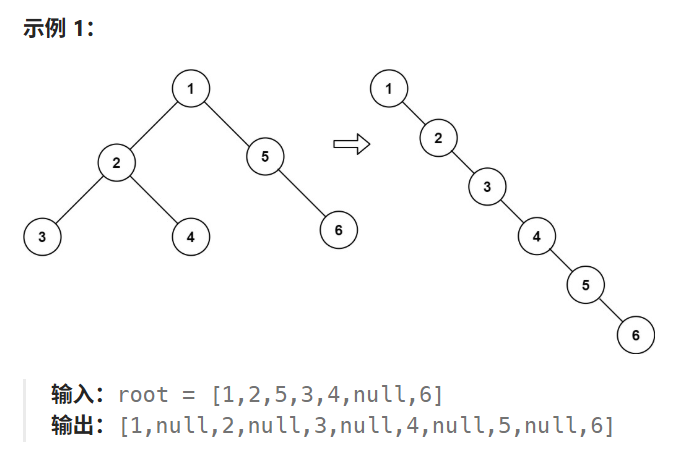
需要在不使用额外存储空间的情况下，直接在原二叉树上进行操作。可以使用莫里斯遍历（Morris Traversal）的思想来实现。

莫里斯遍历的核心思想：

莫里斯遍历利用了二叉树的空闲指针（左子树为空时的左指针），将其指向右子树的前驱节点，从而实现中序遍历。我们也可以利用类似的思路来展开二叉树为单链表。

算法步骤：

1.找到左子树的最右节点：

从当前节点的左子树开始，一直向右走，直到找到最右节点。
这个最右节点是左子树的最后一个节点。

2.调整指针：

将最右节点的右指针指向当前节点的右子树。
将当前节点的左子树移到右子树的位置。
将当前节点的左指针置为 null。

3.移动到下一个节点：

每次处理完一个节点后，current 指针移动到当前节点的右子树。

时间复杂度：O(n)，每个节点最多被访问两次。

空间复杂度：O(1)，不使用额外的存储空间。

下面通过一个具体的例子来模拟原地算法（莫里斯遍历）的过程：

初始状态

current 指向根节点 1

第一步：处理节点 1

检查左子树：节点 1 有左子树，左子树的根是 2。
找到左子树的最右节点：从 2 开始，向右走，找到最右节点 4。

调整指针：
将 4 的右指针指向 1 的右子树（即 5）。
将 1 的左子树移到右子树的位置。
将 1 的左指针置为 null。

调整后的状态：

current 移动到 2

第二步：处理节点 2

检查左子树：节点 2 有左子树，左子树的根是 3。
找到左子树的最右节点：从 3 开始，向右走，没有右节点，最右节点是 3。

调整指针：
将 3 的右指针指向 2 的右子树（即 4）。
将 2 的左子树移到右子树的位置。
将 2 的左指针置为 null。

调整后的状态：

current 移动到 3

第三步：处理节点 3

检查左子树：节点 3 没有左子树。
移动到右子树：current 移动到 3 的右子树，即 4。

第四步：处理节点 4
检查左子树：节点 4 没有左子树。
移动到右子树：current 移动到 4 的右子树，即 5。

第五步：处理节点 5
检查左子树：节点 5 没有左子树。
移动到右子树：current 移动到 5 的右子树，即 6。

第六步：处理节点 6
检查左子树：节点 6 没有左子树。
移动到右子树：current 移动到 6 的右子树，但 6 没有右子树，所以 current 变为 null，结束循环。

最终状态
1 -> 2 -> 3 -> 4 -> 5 -> 6

Java 代码实现：

class Solution {
    public void flatten(TreeNode root) {
        TreeNode current = root;
        while (current != null) {
            if (current.left != null) {
                // 找到左子树的最右节点
                TreeNode pre = current.left;
                while (pre.right != null && pre.right != current) {
                    pre = pre.right;
                }

                if (pre.right == null) {
                    // 将当前节点的右子树接到左子树的最右节点
                    pre.right = current.right;
                    // 将左子树移到右子树的位置
                    current.right = current.left;
                    // 将左子树置为 null
                    current.left = null;
                }
            }
            // 移动到下一个节点
            current = current.right;
        }
    }
}

来源链接：https://www.cnblogs.com/Junjunyi/p/19039681

评分

欢迎为Ta评分